Dictionnaire de base du vocabulaire des mathématiques T

Table ou tableau: nombres organisés en lignes et colonnes.
– ex. une feuille de calcul informatique sur tableur (type Excel, par exemple);
Table de nombres ou de toute entité mathématique.
Plus généralement une liste d'informations organisées en tableau.
– v. Table des symboles mathématiques, tableau périodique des éléments
– a. Table

Table numérique: tableau montrant la mise en relation de deux entités numériques, comme un angle et son sinus pour la table des valeurs trigonométrique.
– v. Tables – Index
– a. Mathematical table

Table de multiplication: tableau donnant les multiplications des nombres de 1 à 9 (parfois jusqu'à 12).
– ex. La table du 9 est facile à apprendre (illustration). Le chiffre des dizaines est égal au nombre multiplié moins "1" et le chiffre des unités est son complément à 9.
– a. Multiplication table, times table

Table de Pythagore: synonyme de table de multiplication présentée en tableau unique (tableau à double entrées) (Illustration pour 1 à 5).
– v. Pythagore
– a. Table of Pythagoras

Table de Cayley: tableau à double entrées donnant les résultats des lois de composition.
Sorte de généralisation de la table de Pythgore.
– v. Vocabulaire des structures algébriques
– a. Cayley table

Table de vérité: tableau donnant les résultats d'opérations logiques.
– a. Truth table

Tableau croisé dynamique (TCD)*: outil de synthèse proposé par les tableurs.
Le « TCD » regroupe les données selon un ou plusieurs critères, et les présente sous forme de sommes, moyennes, comptages, etc.
– a. Pivot table

Matrice: objet mathématique en forme de tables lignes-colonnes.
Outil qui permet de définir globalement des opérations sur une grande quantité de nombres à la fois.
On peut calculer avec des objets de plus en plus sophistiqués: nombres, vecteurs, matrices, tenseurs.
– a. Matrix, matrices

Carré magique: table de nombres dont la sommes sur lignes colonnes et diagonales est constante.
– v. Carrés magiques, Sudoku
– a. Magic square

TABLES NUMÉRIQUES sur ce site: Voir Tables – Index

Tableur: feuille de calcul présentant des tables de nombres sur lesquelles il est possible d'effectuer des calculs (type Microsoft Excel ou Open Office Calc par exemple).
– v. Tableur
– a. Spreadsheet

Tangage: mouvement d'avant en arrière d'un véhicule (navire, avion).
– v. Degrés de liberté, roulis, lacet
– a. Pitch, roll and yaw

Tangente: la droite comme "posée" sur le cercle, par exemple, elle le touche en un seul point.
Elle est perpendiculaire au rayon aboutissant en ce point de "touche", dit point de contact.
La tangente est la position limite d'une droite passant par deux points d'une courbe, lorsqu'un les points d'intersection se rapprochent indéfiniment en restant sur la courbe.
Droite ou courbe en contact avec une courbe en un point et qui fait un angle nul avec elle en ce point.
– étym. du latin tango, tangere toucher.
– v. Tangente, Éléments de base de la géométrie
– a. Tangente: a straight line through a point on a curve that has the same direction at that point as the curve

Tangente (tan ou tg): en trigonométrie, dans un triangle rectangle et pour l'un des angles, valeur du rapport du côté opposé au côté adjacent.
La cotangente est l'inverse de la tangente
– notation: tan ou tg = sinus / cosinus;
cotan ou cot = cosinus / sinus = 1 / tangente.
– ex. tan 45° = 1.
– v. Tangente, sinus, trigonométrie
– a. Tangent, cotangent

Tangente hyperbolique: elle est à l'hyperbole, ce que la tangente classique est au cercle.
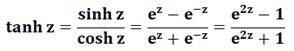– v. Tangente hyperbolique
– a. Hyperbolic tangent

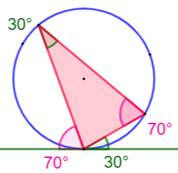
Tangentiel (angle -): dans un cercle, angle entre une corde et la tangente en extrémité de corde.
Le théorème des angles tangentiels exprime l'égalité entre angles inscrits et tangentiels (Illustration)
– a. Alternate segment theorem or tangent chord theorem: the angle between a chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment.

Triangle tangentiel: triangle formé par les tangentes au cercle circonscrit d'un triangle dont les points de tangences sont les sommets du triangle.
– propriété: Le cercle inscrit de ce triangle est aussi le cercle circonscrit du triangle de référence.
– v. Symédiane et triangle tangentiel
– a. Tangential triangle

Polygone tangentiel ou circonscriptible: polygone circonscrit au cercle circonscrit d'un polygone de référence.
Chacun des côtés est une tangente au cercle.
Le nouveau polygone a autant de côtés que celui de référence.
Le losange est un cas particulier du quadrilatéral tangentiel.
Illustration: quadrilatère tangentiel (tangential quadrilateral).
– a. Tangential polygon: The polygon formed by the lines tangent to the circumcircle of a polygon

Tau: constante égale à 2 π = 6,28318530717958647692528676655….
Son utilisation simplifie certaines formules.
En particulier pour désigner les fractions de tour:
– ex. 1/10 tour = τ /10 et non: 2π/10 = π/5

Tautologie: le fait de redire la même chose.
– Syn. Lapalissade, truisme
– a. Truism, tautology, lapalissade

Taux: quantité exprimée en pourcentage.
– ex. Le taux d'intérêt est passé à 2%
– v. Pourcentage, rapport, proportion, règle de trois
– a. Rate.

Télescopique (somme -): somme dont les termes s'annulent de proche en proche.

Télescopage (simplification par -): simplification en présence d'une somme télescopique.
– ex. (10 – 9) + (9 – 8) + (8 – 7) = 10 – 7 = 3.
– v. Exemple / Autre exemple / Exemple avec la somme des inverses des produits / Exemple avec des factorielles / Exemple de la somme des produits d'inverses
– a. Cancelling out, telescoping sum

Templex: outil développé par le CNRS qui permet de comparer les performances de modèles mathématiques notamment lié au climat et ses impacts.

Dans ce domaine précisément, il existe une vingtaine de modèles. Bien qu'ils aient tous une formulation basée sur les équations qui gouvernent les fluides, ils diffèrent sur plusieurs aspects: la modélisation des aérosols, la dynamique glaciaire ou des océans, entre autres processus. On parle d'une Babel des modèles.
Le templex remplace la théorie des nœuds par la topologie algébrique qu'il combine avec la théorie des graphes pour prendre en compte le flot. Il peut être vu comme une espèce de kirigami dynamique, un "dessin découpé" fait des morceaux qui se collent en tenant compte de la direction du flot. Sa découverte apporte un formalisme mathématique longtemps recherché pour décrire les dynamiques dont la dimension est supérieure à trois, comme c'est souvent le cas des phénomènes réels tels que les écoulements océaniques ou la circulation atmosphérique. Source Techno-Science.net

Temps: temps instantané noté t.
intervalle de temps ; très très petit intervalle de temps
– unité SI: la seconde.
– v. Temps, seconde, relativité

Tendance (paramètres de -): en statistiques, regroupe les notions telles que mode, moyenne, médiane et quartiles.
– v. Statistique
– a. Regression analysis, regression parameters

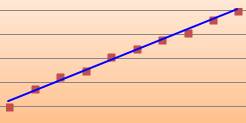
Courbe ou droite de tendance: courbe (polynôme) qui approxime "au mieux" une série de données statistiques.
– v. Régression
– a. Linear regression, polynomial regression

Tenseur** grandeur mathématique ayant beaucoup de composantes.
– ex. Expression des contraintes (tensions) en tout point d'un matériau.
Les vecteurs sont des tenseurs d'ordre 1 et les matrices d'ordre 2. En gros, car le tenseur implique une idée d'organisation des donnés.
– intérêts en théorie de la relativité, mécanique des fluides, élasticité …
– v. Tenseur, arche, tenseurs et champs
– a. Tensor: an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space.

Tenseur métrique**: caractérise une surface en n dimensions.
– v. Riemann

Terme: chacun des éléments d'une somme, d'une suite, d'une série, d'un polynôme, d'un couple; du latin terminus borne, limite.
– v. Addition, soustraction, sommant
– a. Term, addent, an operand to the addition operator. Term of a summation, a polynomial, or a series, a special case of a summand

Tessellation (tesseller): Décomposition d'une surface en éléments de base réguliers disposés bord-à-bord.
– étym. Du latin: tessellare paver de mosaïques
– syn. Pavage, frise
– a.Tessellation, tiling

Tesseract: autre nom de l'hypercube.
– a.Tesseract

Tétraèdre: polyèdre à quatre faces.
Les faces sont nécessairement triangulaires.
Pyramide à base triangulaire (Illustration).
– v. Tétraèdre
– a. Tetrahedron

Tétragone: vieux nom pour quadrilatère.
Nom du carré par les Grecs. En fait, le carré est un tétragone régulier.
– v. Quadrangle
– étym. Du grec tetra gonia quatre angles. Formé comme pentagone, hexagone, etc.
– genre: masculin pour les maths; féminin pour la botanique: sorte d'épinard.
– a. Tetragon

Tétraktys: figure en triangle représentant le nombre 10 par dix points arrangés en quatre lignes de 1, 2, 3 et 4 points.
– v. Tétraktys de Pythagore
– a. Tetractys or tetrad: a triangular figure.

Tétration**: (de quatre fois l'itération)
Opérateur des puissances à étages:
L'exposant en avant de 5 indique la quantité de copies du 5.
Attention à la règle de calcul: on traite les puissances du haut vers le bas.
– ex.
– v. Tétration, autres notations (Knuth, Conway, Graham)
– a. Tetration or hyper-4 or superexponentiation or power tower

Thalès (théorème de -): affirme la conservation des proportions sur des sécantes coupées par des droites parallèles.
– v. Théorème de Thalès, homothétie
– a. Intercept theorem / Thales' theorem / Basic proportionality theorem.

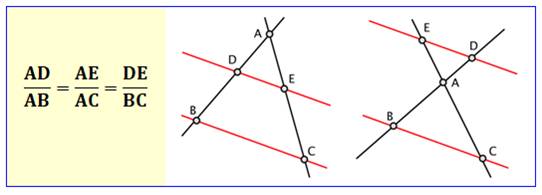
Soit un triangle ABC, et deux points D et E des droites (AB) et (AC) de sorte que la droite (DE) soit parallèle à la droite (BC). Alors on a :

Théodolite: instrument servant à mesurer les angles.
Les angles horizontaux avec le goniomètre et les angles verticaux avec l'éclimètre.
– a. Theodolite: a precision optical instrument for measuring angles between designated visible points in the horizontal and vertical planes.

Théorème: proposition, dite conclusion, qui est démontrée à partir d'axiomes ou d'autre théorèmes déjà démontrés.
Une assertion démontrée.
Une conséquence déduite d'un théorème est un corollaire.
– étym. Du latin theorema théorème, proposition; du grec theorein contempler, examiner.; theorêma: spectacle, fête, objet digne d'étude.
– v. Démonstration, théorème, axiome, hypothèses, démonstration, lemme, postulat, incomplétude
– a. Theorem

Théorème des milieux: dans un triangle, le segment qui joint les milieux de deux côtés d'un triangle est parallèle au troisième côté et est égal à sa moitie en longueur.
La réciproque est vraie.
– v. Théorème des milieux.
– a. Midpoint theorem: the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the third side.

Pythagore (théorème de -): dans un triangle rectangle: a² + b² = c², a, b et c étant la longueur des côtés.
Aussi nommé: "pont aux ânes".
La réciproque est vraie.
– v. Théorème de Pythagore et ses nombreuses démonstrations, triplets de Pythagore

Thalès (théorème de -): Voir Thalès
– v. Théorème de Thalès, homothétie
– a. Intercept theorem, Thales' theorem, basic proportionality theorem

Théorème fondamental de l'arithmétique*: la factorisation d'un nombre est unique.
– ex. 111 = 3 x 37, 100 = 2² x 5²
– v. Théorème fondamental de l'arithmétique, facteurs et diviseurs

Théorème fondamental de l'algèbre* ou théorème de d'Alembert-Gauss: Une équation du nième degré a toujours n racines, réelles ou complexes.
Tous les polynômes peuvent être factorisés en utilisant les nombres complexes.
Un polynôme de degré n aura n facteurs.

Théorème fondamental de l'algèbre ou théorème de d'Alembert-Gauss:
Le théorème indique que tout polynôme non constant, à coefficients complexes, admet au moins une racine.
Ce qui induit cette propriété: tout polynôme non constant, à coefficients complexes, de degré n a exactement n racines, chacune étant comptée avec son ordre de multiplicité.
The fundamental theorem of algebra (the d'Alembert-Gauss theorem) is stated as follows: every non-zero, single-variable, degree n polynomial with complex coefficients has, counted with multiplicity, exactly n complex roots.

Théorie: ensembles de théorèmes à partir d'axiomes, de vérités premières admises.
– a. Theory

Théorie des nombres** prolongement de l'arithmétique: étude des propriétés profondes des nombres.
Utilisation des nombres comme concepts abstraits.
Étude des fondements, des théorèmes, d'une systématique des nombres.
– v. Théorème de la théorie des nombres
– a. Number theory

Théorie mathématique: un ensemble d'axiomes muni d'un certain nombre de règles logiques permet de construire une théorie mathématique.
– v. Théorie
– a. Mathematcal theory

Théorie de l'information*: partie des mathématiques qui s'intéresse à la transmission des données.
Notamment, comment mesurer l'information.
Cette théorie vise donc à quantifier et qualifier la notion de contenu en information présent dans un ensemble de données.
– v. Claude Shannon
– a. Informaton theory: the scientific study of the quantification, storage, and communication of digital information

Théorie des ensembles: étude des ensembles.
– a. Set theory

Théorie des graphes: étude des graphes.
– a. Graph theory

Théorie algorithmique des nombres: vise à trouver des méthodes pratiques et efficaces en théorie des nombres: factorisation, calcul de PGCD, multiplication rapide, etc.
– a. Algebraic number theory uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations.

Autres: Théorie des groupes / Théorie des probabilités / Théorie des jeux / Théorie de la complexité / Théorie du chaos / Théorie des cordes / Théorie axiomatique / …

Tierce majeure: deux notes sont dans un rapport de tierce majeure si la fréquence de l'une est dans le rapport 5/4 de l'autre.
Elle correspond à un intervalle de quatre demi-tons.
– v. Gamme, octave, quinte, tierce
– a. Major third

Tierce mineure: le rapport est 6/5.
Elle correspond à un intervalle de trois demi-tons.
– v. Gamme, octave, quinte, tierce
– a. Minor third

Tiers: fraction qui vaut 1/3 = 0,333…;
– à noter: Pour passer du tiers à la moitié (demi), il faut ajouter 1/6
– v. Nombre 0,333…
– a. Third: The fraction 1⁄3, one of three equal parts
– attention: Third signifie aussi: le troisième => 3rd is the ordinal form of the cardinal number 3.

Tiers exclu (principe du -): une proposition est vraie ou fausse, pas d'autre possibilité.
– notation: La proposition est vraie. Lire: (p ou non-p).
– v. Tiers exclu Logique, contradiction, absurde;
– a. Law of excludes middle

Tonne: vaut 1 000 kg.
– v. Unités de masse, quintal, nombre 1000

Topologie: étude des propriétés géométriques se conservant par déformation continue.
Généralisation aux notions de limite et de voisinage.
– v. Topologie, espaces topologiques
– a. Topology

Tore: solide engendré par la rotation d'un disque autour d'un axe situé dans le même plan.
– volume: avec r le rayon du cercle et R la distance de l'axe au centre du cercle (le rayon du tore).
– v. Tore
– a. Torus (several tori), shape of a donut

Torseur:.mot qui a à voir avec tordre, torsades. Utilisé en mécanique (statique du solide) pour décrire les mouvements des solides et les actons mécaniques qu'ils subissent. Imaginez le champ de vecteurs d'un solide en rotation, par exemple.
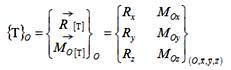Il définit une action mécanique en spécifiant la force résultante R et le moment M en un point donné et pour le mouvement d'un solide m par rapport à un solide n.
– ne pas confondre avec Tenseur
– a. screw theory

Total: synonyme de somme: résultat d'une addition.
– ex. le total des dépenses
– a. Total: the summation of a set of numbers;
– notez: la somme totale (!), the total amount

Totient* ou indicatrice d'Euler d'un nombre entier n.
Quantité de nombres premiers avec n et inférieurs à n.
– a. Euler totient function

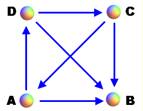
Tournoi: graphe complet et orienté. Il représente un tournoi ou chaque participant rencontre chacun des autres.
L'orientation indique qui a battu qui, qui domine qui. Voir Illustration pour quatre participants.
– v. Tournoi
– a. Tournament

Traine*: en statistiques, partie en queue de la courbe de distribution.
Partie éloignée de la valeur centrale.
– a. Tail

Longue traine ou long tail en statistiques: la plus grande partie de la distribution est contenue dans cette traine (par rapport à une loi normale).

Longue traine ou long tail en économie: vente d'une grande variété de produits, chacun en petite quantité. Exemple: Amazone.
v. Longue traine

Traitement de données: exploitation de données par ordinateur selon un algorithme.
– ex. Traitement des données d'heures de travail pour calculer la paye des employés; ex: traitement des données d'images pour construire un paysage virtuel sur l'écran.
– v. Signal analogique et sa numérisation, filtrage spatial, compression
– a. Data processing

Traitement de signal: ensemble des techniques visant à modifier un signal pour en extraire une information.
Regroupe les techniques de traitement, d'analyse et d'interprétation des signaux: filtrage, réduction de bruit, compression, transmission, détection, classification, etc
– a. Signal processing.

Trajectoire: ligne décrite par un point en mouvement.
S'agissant d'un objet, le point suivi est souvent le centre de gravité.
En mécanique, on appelle trajectoire du point P dans un mouvement, par rapport à une repère R, l'ensemble des points coïncidants de l'espace d'observation.
– ex. la trajectoire d'un avion, d'un projectile.
– a. Trajectory or flight path

Trammel ou ellipsographe: instrument articulé qui sert à tracer des ellipses.
– v. Construction des ellipses
– a. Trammel or Achmedes

Transcendant (nombre -): qui ne peut pas être défini par une équation.
Jamais racine réelle ou complexe d'un polynôme non nul.
Pi (p) est un nombre transcendant.
Parmi les nombres (réels ou complexes), on trouve les nombres transcendants et ceux qui ne le sont pas, dits algébriques.
– v. Nombres transcendants, constante e, Oméga
– a. Transcendental number: a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients

Équation transcendantale: équation sans solution analytique. Résolution par approximations successives.
– Voir exemples: Résolution d'équations transcendantales / Problème de la citerne remplie au quart.
– a. Transcendental equation

Fonction transcendantale: fonction non-algébrique, c'est-à-dire qu'elle n'est pas solution d'une équation polynomiale à coefficients polynomiaux par rapport à ses arguments.
– ex. sinus, cosinus, log, x^π, x^x …
– a. Transcendental function

Transfinis* des infinis encore plus grand que l'infini.
– v. Transfinis, Aleph, diagonale de Cantor
– a. Transfinite number

Transformation: opération qui modifie une figure par déplacement ou changement d'échelle ou passage à travers des miroirs.
Une transformation se modélise généralement par une fonction.
Une transformation T du plan associe à tout point M un point M', appelé image ou transformée de A par la transformation.
Pour tout point M', il existe un unique point M dont M' est l'image par T.
Une transformation est une bijection d'un espace sur lui-même.
Une application du plan ou de l'espace sur lui-même associant deux objets géométriques, points ou figures.
Les transformations principales sont les translations, les rotations, les symétries et les homothéties.
– v. Similitude, isométrie, homologie
– v. Transformation, transformations du triangle
– a. Transformations can be classified as direct or indirect. The direct isometries are rotation and translation. They are called direct because they do not flip (or turn over) the shape being transformed. Reflection and glide reflection are indirect isometries because they do flip the shape being transformed.

Transformation conforme: qui conserve les angles, mais pas nécessairement les longueurs.
– a. Conformal map

Transformée: figure obtenue suite à une transformation.
Image de la figure d'origine.
Plus généralement: association d'un fonction à une autre fonction sur un domaine éventuellement différent.
– a. Transformation function. A transformation changes a figure into another figure. The new figure formed by a transformation is called the image.

Transformée de Fourier*: Outil pratique qui permet de faire des calculs sur des fonctions bizarroïdes, mais répétitives. Celles-ci sont transformées en sommes de fonctions périodiques (sinus et cosinus) plus simples.
Généralisation du développement en série de fonctions non- périodiques.
Transformée de Fourier
– a. Fourier Series / Fourier Transform

Transposée d'une matrice: matrice obtenue en interchangeant lignes et colonnes.
– notation: M^T– a. Transpose of a matrix; M^T is obtained by interchanging the rows and columns of a given matrix M.

Transistor: dispositif électronique (semi-conducteur) à trois "pattes": deux pour l'entrée-sortie du courant et une troisième (base) pour gérer le passage du courant en l'amplifiant plus ou moins.
Phénomène proche de l'homothétie ou le niveau de tension sur la base jouerait le rôle du rapport d'homothétie.
– étym. Mot-valise anglais: transfer et resistor
– v. Diode
– a. Transistor

Transitive, transitivité: propriété qui se transmet de proche en proche, en cascade.
– ex. Albert est plus grand que Baptiste et Baptiste est plus grand que Charles, alors Albert est plus grand que Charles.
Une relation est transitive si .
– v. Symétrique, réflexive, relation d'ordre, déduction, vocabulaire des structures algébriques
– a. Transitive relation

Translation: déplacement d'une figure dans un plan par glissement dans une direction donnée.
Pas de rotation ni de retournement.
Un vecteur définit complètement la translation.
Un point M et son image M' par une translation de vecteur AB, forment un parallélogramme avec les points A et B.
Soit un vecteur du plan, on appelle translation de vecteur la transformation qui à tout point M du plan associe le point M’ tel que ;
– v. Translation.
– a. Translation: transformation that moves every point of a figure, shape or space by the same distance in a given direction.

Translation en mécanique: Un objet 2 est en translation par rapport à un objet 1 si et seulement si toute droite de l'objet 2 conserve, par rapport à l'objet 1, une direction constante au cours du temps.

Transposition: faire passer un terme de l'autre côté du signe "égal" dans une égalité.
– ex. ax = b en transposant b devient ax – b = 0.

Transposition (sur un ensemble E): permutation de E qui échange deux éléments de E et laisse invariants tous les autres.
– a. Transposition: a permutation which exchanges two elements and keeps all others fixed.

Transposition d'une matrice (transposée): permutation des éléments telle que une matrice A "portrait" devient une matrice "paysage" A^T.
– ex: une matrice 2 lignes 4 colonnes devient une matrice avec 4 lignes et 2 colonnes.
Pour chaque élément b_{i j}= a_{j i}
– a. Transposition of a matrix, to produce the transpose of a matrix

Transversale: dans un carré latin, ensemble des cellules correspondant à un élément choisi.
Pour chaque transversale, cet élément se retrouve sur des cellules et des colonnes différentes.
– v. Transversale, permutation figurée, motifs des tissus
– a. Lucas permutation

Trapèze: quadrilatère dont deux côtés sont parallèles.
Il est rectangle si un des angles est droit.
– étym. Du grec trapezion, petite table.
– v. Trapèze
– a. Trapezoid: at least two opposite sides are parallel.
Two parallel sides, and no line of symmetry
Américain: Trapezoid / Anglais: Trapezium

Trapèze isocèle: les côtés non parallèles sont de même longueur.
– a. Isosceles trapezoid

Trapèze rectangle: avec un angle droit.
– a. Right trapezoid

Trapézoèdre, antidiamant ou deltoèdre: Polyèdre dont toutes les faces sont des quadrilatères symétriques.
Les faces sont alors des losanges ou des cerfs-volants.
– a. Trapezohedron, antidipyramid, deltohedron

Treillis: graphe de forme carrée, comme un grillage.
– ex. La représentation des nombres binaires en treillis, chemins sur réseaux

Treillis** Ensemble ordonné dans lequel tout couple d'éléments admet une borne supérieure et une borne inférieure.
– ex. Tout ensemble totalement ordonné est un treillis; Un ensemble muni de l'inclusion est un treillis dont la borne inférieure est l'intersection de deux ensembles et la borne supérieure est leur réunion.
– a. Lattice

Treillis de Tamari**: définit par Dov Tamari Il définit les treillis de Tamari dont les éléments sont les différentes façons de grouper les éléments d'une séquence par paires en utilisant des parenthèses.
– v. Treillis de Tamari
– a. Tamari lattices

Dans sa vision, Tamari considérait l'ensemble des séquences entre crochets comme un ensemble partiellement ordonné, et il considérait également ce poset comme le squelette d'un polytope convexe. Cet ensemble partiellement ordonné est maintenant appelé le réseau ou treillis de Tamari.

Triangle: figure géométrique plane à trois côtés.
Polygone à trois côtés,
– syn. trigone, trilatère.
– étym. Du latin triangulum, de tres, trois, et angulum, angle.
– vocabulaire du triangle: scalène, rectangle, isocèle, équilatéral, acutangle, obtusangle, semblables, égaux, curviligne, sphérique, etc.
– v. Triangle, Types de triangles
– a. Triangle: a polygon with three edges and three vertices.

Somme des angles du triangle: elle est toujours égale à 180°
– v. Somme 180°
– a. Angles in a triangle sum to 180°

Droites concourantes du triangle: intersection entre trois céviennes remarquables du triangle, comme: hauteur, bissectrice, médiane et médiatrice
– v. Céviennes
– a. Cevian

Théorème de Ceva: propriété des proportions découpées sur les côtés par trois céviennes concourantes.
– v. Théorème de Ceva
Ceva's theorm

Triangles et cercles
– v. Cercles et triangles, circonscrit, inscrit, exinscrits
– a. Circumcicle, incircle, excircle

Triangle de Pascal ou triangle arithmétique: tableau de nombres organisé en triangle, chacun des nombres spécifiant un coefficient binomial, autrement-dit la quantité de choix de k parmi n.
– v. Triangle de Pascal
– a. Pascal's triangle

Triangle (nombre -): nombre géométrique figuré par un triangle.
– ex. 1, 3, 6, 10 …
– v. Nombres triangulaires.

Triangulaire (inégalité -): dans un triangle, un côté est plus petit que la somme des longueurs des deux autres côtés.
Dans une somme de vecteurs, les normes sont telles que .
Généralisation évidente à un segment AB et un point quelconque M, aller de A à B est toujours plus court que le trajet AMB.
– v. Inégalité triangulaire
– a. Triangle inequality

Triangulaire (matrice -): une matrice triangulaire supérieure et une matrice carrée dont tous les termes situés en dessous de la diagonale principale sont nuls. Elle est triangulaire inférieure si ce sont tous les termes situés au-dessus de la diagonale principale qui sont nuls.

Triangulation: méthode utilisée par les géomètres pour déterminer la position d'un élément géographique à partir de la connaissance de deux autres.
– v. Triangulation, dissection, trilatération

Triangulation du polygone: pavage d'une figure polygonale avec des triangles jointifs; leur union recouvre le polygone.
Technique souvent utilisée pour modéliser un objet et pour le restituer en images calculées, par exemple.
– v. Triangulation des polygones
– a. Polygon triangulation: decomposition of a polygonal area into a set of triangles.

Triangulation d'une surface*: décomposition d'un polygone en triangles avec un nombre maximal de diagonales sans intersection. Généralisation à la dimension 3 et au-delà
– v. Triangulation des polygones
– a. A triangulation of a polygon P is a decomposition of P into triangles by a maximal set of non-crossing diagonals.

Trièdre: figure dans l'espace formée par trois plans qui se coupent deux à deux.
– propriété: Trois plans qui passent en un même point divisent l'espace en huit angles trièdres deux à deux opposés par le sommet.
Un trièdre rectangle est un trièdre dont les trois axes (et les trois plans) sont deux à deux perpendiculaires.
– v. Dièdre
– a. Trihedron: a figure determined by the intersection of three planes.

Trièdre (adj.): qui a trois faces places.
– ex. une pyramide trièdre

Angle trièdre: angle formé par l’intersection de trois plans.

Trièdre orthonormé: désigne une base orthonormée.
– a. Orthonormal basis: a basis whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other.

Trigone: voulait dire triangle chez les Grecs.
Qui possède trois angles.
– a. Trigon: a polygon with three sides.

Trigonométrie*: outils mathématiques qui permettent notamment de calculer des longueurs et des angles dans les triangles quelconques.
Ensemble des propriétés des fonctions circulaires.
– ex. Du grec trigônon, triangle et metron mesure.
– v. Trigonométrie, relations trigonométriques, tables trigonométriques
– a. Trigonometry

Trigonométrique (sens –): rotation dans le sens inverse des aiguilles d'une montre
– v. Antihoraire, angle de rotation
– a. Counterclockwise (CCW)

Fonctions trigonométriques: principalement sinus, cosinus, tangente, cotangente (illustration)
– v. Les trois principales
– a. Trigonometric functions

Trilatération*: méthode particulière de triangulation. Contrairement à la triangulation, qui utilise les angles et les distances pour positionner un point, la trilatération utilise les distances entre un minimum de deux points de référence.
Utilisation notamment par le GPS.
Utilisé aussi en robotique (Robot positioning using an enhanced trilateration algorithm).

Trilatère: polygone à trois côtés ou, plus généralement, objet à trois côtés.
Nom vieilli pour triangle.

Trilatéral: adjectif pour: qui a trois côtés.
Comme: bilatéral, quadrilatéral.
– a. Trilateral

Trilittère: composé de trois lettres.
– v. Quantité 3

Trilinéaire (coordonnées -)**: triplet de nombres indiquant la distance d'un point à chacun des côtés d'un triangle.
– v. Coordonnées trilinéaires, coordonnées trilinéaires et énigmes de transvasement
– a. Trilinear coordinates

Trillion: 10^3x6 = 10¹⁸;
– attention: en anglais vaut 10^3x3+3 = 10¹², soit le billion français.
– v. Noms des grands et petits nombres, zillion

Trinôme: polynôme à trois termes (a + 2b + 3c, a² + 6b³ – 17c).
– v. Monôme, binôme
– a. Trinomial: a three-term polynomial

Trinôme du second degré: ax² + bx + c
– v. Équation du second degré, les trois formes du trinôme
– a. Quadratic equation

Triparti (graphe -): graphe comprenant trois séries de sommets.
– v. Biparti
– a. Tripartite graph, 3-partite graph

Triplet: trois éléments, noté (x, y, z).
– v. Doublet, quadruplet, repère, triplet de Pythagore réciproque, k-tuple, k-tuplet
– a. Triple

Triplet de Pythagore: trois nombres entiers tels que a² + b² = c².
– ex. 3² + 4² = 5² ; 33² + 56² = 65²
– v. Triplet de Pythagore
– a. Pythagorean triple: three positive integers a, b, and c, such that a² + b² = c².

Trirectangle (trièdre): les trois arêtes du trièdre sont perpendiculaires deux à deux.
Référentiel pratique pour l'espace usuel à trois dimensions (3D).

Trisection: division en trois parties égales.
Célèbre problème antique visant à découper un angle en trois parties égales.
– v. Trisection, théorème de Morley, bissectrice, duplication, quadrature
– a. It is impossible to square the circle by compass and straightedge.

Trivial: synonyme de banal, évident, qui ne présente aucun intérêt, ne mérite pas que l'on s'y attarde.
– ex. l'équation x(x² - 5x + 6) = 0 admet une racine triviale x = 0 et deux racines un peu plus difficiles à trouver x = 2 et x = 3.

Étymologie: du latin trivium, embranchement à trois voies.

En anglais le latin trivialis a donné également un adjectif trivial au sens de « commun, banal, familier », puis, plus particulier, « négligeable, peu important », d'où son emploi en math pour qualifier des données sans importance ni intérêt, par exemple si elles sont égales à zéro ou présentent des caractéristiques de relation ou d'identité qui les rendent non conséquente (Source CNTRL).

Trois: 3
– v. Nombre 3
– a. Three

Trois (règle de -): méthode pour trouver le quatrième terme parmi quatre termes ayant un même rapport de proportion lorsque trois de ces termes sont connus.
– v. Pourcentage, rapport, proportion, prorata, fraction, multiplication
– a. Cross multiplication, "cross your heart"

Troisième degré (équation du -)* ou cubique:
Équation du type: .
– v. Équation du 3^e degré
– a. Cubic equation

Tronc d'un solide: une des parties du solide entre deux plans parallèles.
– a. Frustum

Tronc de cône ou de pyramide: le plan sécant est parallèle à la base.
– v. Tronc de cône
– a. Cone or pyramid frustum

Tronc de prisme ou de cylindre: le plan sécant est quelconque.
– v. Prisme, cylindre.

Tronquer, troncation, troncature: supprimer la partie décimale d'un nombre.
– ex. 12,45 devient 12.
– ex. de calcul: ,
cette suite de calculs permet d'isoler l'unité (2) d'un nombre (ici 12).
– v. Tronquer
– a. Trunc

Troncature à n décimales: on conserve les n premières décimales.
– ex: La troncature de Pi au centième est 3,14.
– v. Partie entière, INT

Truisme: synonyme d'évidence. Chose triviale.
Dire que "deux et deux font quatre" est un truisme.
– Syn. Lapalissade, tautologie
– a. Truism, tautology, lapalissade

Tuple: dans le langage Python: une suite immuable d'éléments ( = liste fixe).
– Ex: t = 'a', 'b', 'c', 'd', 'e'
– voisins: Ensemble, liste, suite, série
– v. Vocabulaire Python
– a. Tuple

n-tuple: k éléments avec ordre, habituellement distincts.
– v. n-uple
– a. Tuple

Turing (machine de -) **:.
Machine abstraite qui fonctionne comme un ordinateur.
Imaginée par Alan Turing en 1936 pour travailler le concept d'algorithme.
La thèse de Church postule que tout problème de calcul fondé sur une procédure algorithmique peut être résolu par une machine de Turing.
– v. Machine de Turing.
– a. Turing machine: an abstract machine that manipulates symbols on a strip of tape according to a table of rule.

Type (théorie des -) **: Sorte d'alternative à la théorie des ensembles.
Cette théorie permet de contourner le paradoxe de Russell en introduisant tout d'abord une hiérarchie de types, puis en assignant un type à chaque entité mathématique. Les objets d'un certain type ne peuvent être construits qu'à partir d'objets leur préexistant, empêchant ainsi les boucles infinies et les paradoxes de surgir et de casser la théorie.
– a. Type théorie

>>> U

Voir	Atlas des maths – des références Débutants – pour juniors ou novices
Aussi	DicoNombre – tous les nombres de 0 à l'infini DicoLettre – signification des lettres en maths et ailleurs DicoCulture lettre T
Autres	Voir page des liens et références
Cette page	http://villemin.gerard.free.fr/Referenc/Encyclop/T.htm