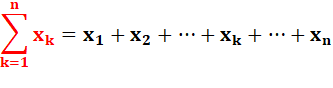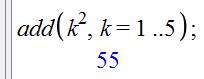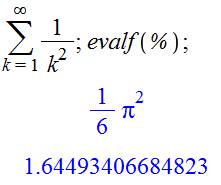NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/09/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Théorie des Nombres
Débutants Division	Opérations			Glossaire Division
INDEX Accueil Sommaire Calcul		Somme	Division	Étrangers (premiers entre eux)
	Terminale Spé
		Sommaire de cette page >>> Addition et somme >>> Symbole de somme d'une suite >>> Somme d'une suite infinie convergente >>> Somme d'une suite infinie non convergente >>> Somme discrète ou continue

SOMME et SOMMATION

Faire une addition, tout le monde connait. Lorsqu'il s'agit de définir correctement le processus d'addition, les choses se compliquent. Encore une coquetterie de mathématiciens … qui amène son lot de surprises.

Addition et somme
Définition Au sens commun, l'addition des éléments de plusieurs ensembles consiste à compter tous les éléments de ces ensembles, comme s'ils avaient été mis en commun dans un grand ensemble. Le compte final est appelé la somme. Si la quantité d'éléments dans un ensemble est appelée son cardinal, alors: Card(1) + Card(2) + Card(3) = Card de l'union des ensembles (1, 2 et 3).	Le paysan a 3 vaches dans un pré, 5 dans un autre et 2 dans le troisième. Il possède: 3 + 5 + 2 = 10 vaches. La ménagère achète 3 carottes, 5 poireaux et 2 tomates. Elle a acheté: 3 + 5 + 2 = 10 légumes.
Méthode de calcul On calcule indifféremment dans l'ordre que l'on veut avec les sommes partielles que l'on veut. On dit que la somme est commutative et associative.	3 vaches + 5 vaches + 2 vaches = 5 vaches + 2 vaches + 3 vaches = (3 vaches + 5 vaches) + 2 vaches = 8 vaches + 2 vaches = (3 vaches + 2 vaches) + 5 vaches = 5 vaches + 5 vaches Etc.

Symbole de somme d'une suite
Notation d'une suite de termes semblables Somme de toutes les valeurs de xk pour k variant de 1 à n.
Exemple Suite des nombres au carré jusqu'à 5.
Programmation avec boucle La méthode la plus classique consiste à exécuter une boucle, un calcul itératif. Algorithme	Programme générique (description de l'algorithme) La mémoire S est initialisé avec la valeur 0. Depuis n = 1 et jusqu'à n = 5, calculer n². Ajoutez ce résulta à la mémoire S. À la fin, affichez la valeur de la mémoire S. Programme Maple
Programme adapté à une suite Cette instruction additionne automatiquement les carrés des nombres de 1 à 5.
Programmation directe La majorité des programmes de calcul mathématiques mettent une instruction spéciale à disposition.

Voir Programmation – Index

Somme d'une suite infinie convergente
Exemple classique Somme des inverses des factorielles. On lit: la somme pour toutes les valeurs de k de 0 à l'infini de l'inverse de la factorielle de k est égale à la constante e qui vaut exponentielle de 1.
Somme des inverses des carrés

Voir Somme des entiers, inverses, … / Somme des inverses des puissances

Somme d'une suite infinie non convergente
Suite paradoxale La suite harmonique est composée de termes qui tendent vers 0, et pourtant la somme infinie tend vers l'infini.
Exemple classique Somme alternée de 1 et – 1. Pour formaliser les éléments de la suite, on porte -1 à la puissance qui convient. Le signe doit être positif pour les rangs impairs et négatifs pour les pairs.		S = 1 – 1 + 1 – 1 + 1 - … Maple donne la valeur 0,5 pour cette somme infinie.
Sommes diverses Le résultat (la somme) diffère selon l'ordre des opérations.	S = (1 + 1 + 1 + …) – (1 + 1 + 1 + …) = 0 S = 1 – (1 – 1) – (1 – 1 ) - … = 1 S = 1 – (1 – 1 + 1 – 1 + 1 - …) = 1 – S Commutativité et distributivité ne s'appliquent pas à ces suites infinies, au risque de produire des résultats disparates.
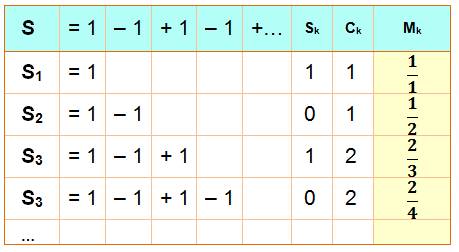
Somme partielles On peut chercher à connaitre la valeur de la somme à chaque fois que l'on ajoute un terme (Sk => 1, 0, 1, 0 …). Le cumul donne: (Ck => 1, 1, 2, 2 …). Ce qui donne une contribution moyenne de chaque somme: (Mk => 1, 1/2, 2/3, 2/4 …). Prolongée à l'infini cette fraction tend vers 1/2.	On cherche à définir une contribution moyenne de chaque somme partielle. Si celle-ci converge vers une valeur limite, on attribue cette valeur limite à la suite infinie.
Le mathématicien Ernesto Cesaro (1859-1906) a proposé que cette limite soit une certaine mesure de la suite infinie.	Muni de cette méthode de sommation, Cesaro étend la notion de convergence et poursuit le travail mathématique avec elle. C'est un réflexe habituel du mathématicien que de chercher à étendre son champ de travail.

Voir La suite qui rend très fou: 1 + 2 + 3 + … = -1/12; et encore plus fou …

Somme discrète ou continue

Nous venons de voir la somme appliquée à l'addition de nombres rationnels. La sommation sur les nombres réels est une intégrale. Les Anciens approchaient ces sommes en prenant des nombres de plus en plus petits, les infinitésimaux. C'est Leibniz et Newton qui ont inventé le calcul différentiel conduisant au calcul intégral.

Suite	Division Suites et séries
Autour	Addition – Initiation La suite qui rend très fou: 1 + 2 + 3 + … = -1/12 Sommes des nombres, des carrés, des cubes … Somme serpentin Divisibilité par un nombre donné Sujets du bac – Index
Voir	Cryptage Des jeux sur les partages Jeux et puzzles – Index L'arithmétique de l'horloger – Congruence / Modulo Le calcul mental Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Referenc/Prof/THdesNBS/Somme.htm