Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 04/06/2023 M'écrire Brèves de Maths

INDEX Graphe Topologie Géométrie Logique Dénombrement Jeux	Nombres et théorème de RAMSEY
	Petits Nombres (Intro.)	Valeurs – Table	EN BREF
	Principe des tiroirs	Propriétés et calculs	R(3, 3) = 6	R(3, 3, 3)
	Assemblée	Bornes – Historique	R(3, 4) = 9	R(5, 3) = 14
	Graphe	Ramsey – Biographie	R(4, 4) = 18

Faites un double-clic pour un retour en haut de page

Nombres de RAMSEY R(3,3,3) = 17 R(3,3,3,3) ≤ 62 Le (3, 3, 3) est le seul nombre multi-Ramsey connu !
	Sommaire de cette page >>> R(3,3,3) >>> Graphe à 16 sommets et trois couleurs >>> R(3,3,3,3) ≤ 62	Débutants Dénombrement Glossaire Combinatoire

R(3,3,3)			haut
Multi-couleur Valeur connue Seule la valeur de R(3,3,3) est connue.		R(3,3,3) Il est possible de dessiner un graphe à 16 sommets sans faire apparaitre un triangle monochromatique: R(3,3,3) > 16 1955: preuve que R(3,3,3,) = 17 par Greenwod et Gleason 1964: ce défi a été lancé aux Olympiades mathématiques internationales. 1985: Sun et Cohen propose une preuve plus simple. On sait que tous ces nombres R(p1, p2, …pk) existent.
Assemblée	Chacun des 17 étudiants parlent avec chacun des autres. Chaque couple d'étudiant discute d'un des trois sujets. Alors, inévitablement, trois étudiants parlent du même sujet entre eux.

Graphe à 16 sommets et trois couleurs

Graphe proposé par Sun et Cohen pour leur démonstration

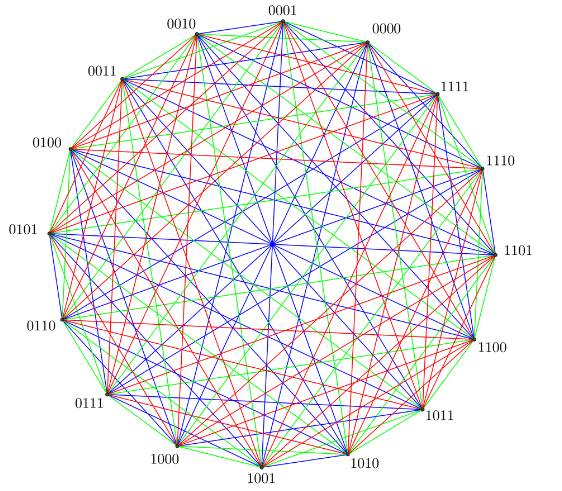
Colorié avec trois couleurs sans former de triangle => R(3, 3, 3) >16

Autre présentation du graphe à 16 sommets

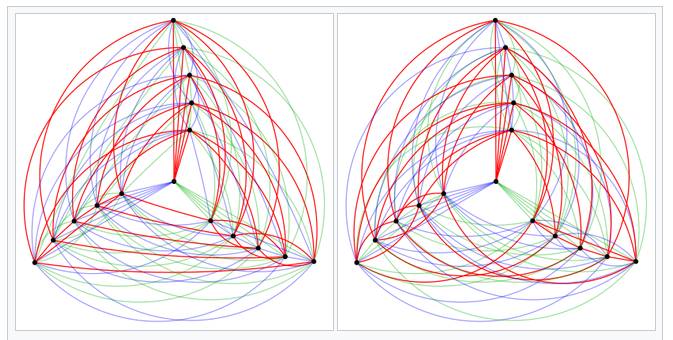
Les deux seuls tels graphes (hors rotations, permutations) sans triangle monochromatique.

Source: A multicolour example: R(3,3,3) = 17 – Wikipedia

R(3,3,3,3) ≤ 62	haut
En 1955, Grennewood et Gleason donne la fourchette: 41 à 66. En 1972, Earl Glen Whitehead propose la fourchette 49 à 65. En 1974, Folkman confirme la borne supérieure à 65. En 1995, Sanchez-Florez descend à 64. En 2006, Richard L. Kramer montre que R(3, 3, 3, 3) ≤ 62. Ce qui veut dire que: pour tout coloriage du graphe complet à 62 sommets avec quatre couleurs, il y aura forcément un triangle monochrome. La démonstration s'appuie sur le résultat connu pour R(3, 3, 3) et notamment la connaissance des deux seuls cas pour 16 sommets vus ci-dessus. L'auteur précise qu'il n'est pas difficile de prouver que: R(3, 3, 3, 3) ≤ 4 × (R(3, 3, 3; 2) – 1) + 1 + 1 = 66 Formule de R. E. Greenwood et A.M. Gleason En 1973, Chung avait montré par construction que R(3, 3, 3, 3) ≥ 51.
Fort de ce résultat pour R(3, 3, 3, 3), et depuis 2002, pour n supérieur à 3, on sait que R(3, 3, …,3n fois ) ≤ n! (e – 1/6) + 1

English corner

Haut de page (ou double-clic)

Retour	Ramsey: R(4, 4) = 18
Suite	Ramsey: R(5, 3) = 14
Voir	Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ	Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ
Sites	Voir Références en page d'introduction Un exemple à trois couleurs – Wikipédia Ramsey's Number R(3, 3, 3) – Cut-the-knot Another Evaluation of the Ramsey number R(3,3,3) – Mathematics The classical Ramsey number R(3, 3, 3, 3) ≤ 62 – Richard L. Kramer
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/R333.htm