Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 04/06/2023 M'écrire Brèves de Maths

INDEX Graphe Topologie Géométrie Logique Dénombrement Jeux	Nombres et théorème de RAMSEY
	Petits Nombres (Intro.)	Valeurs – Table	EN BREF
	Principe des tiroirs	Propriétés et calculs	R(3, 3) = 6	R(3, 3, 3)
	Assemblée	Bornes – Historique	R(4, 3) = 9	R(5, 3) = 14
	Graphe	Ramsey – Biographie	R(4, 4) = 18

Faites un double-clic pour un retour en haut de page

Table des nombres de RAMSEY Les nombres de Ramsey sont très difficiles à calculer. Il serait illusoire de vouloir examiner les cas un par un, car beaucoup trop nombreux. À partir de R(5, 5) on ne connait que des encadrements. Voyez le meilleur encadrement connu pour R(10, 10). Les mathématiciens cherchent à améliorer les bornes pour tout nombre de Ramsey.
	Sommaire de cette page >>> Nombres de Ramsey >>> Table des nombres de Ramsey >>> Historique	Débutants Dénombrement Glossaire Combinatoire

Nombres de Ramsey – Rappel		haut
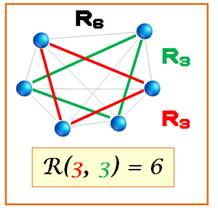
Le graphe complet à six sommets est nommé R6. Ceux à trois sommets: R3. Le nombre de Ramsey en 3, 3 est 6 et on le note: R(3, 3) = 6. Ce qui veut dire qu'avec six points, en coloriant tous les traits avec deux couleurs, il y aura toujours au moins un triangle monochrome, bleu ou rouge. On sait, qu'en fait, il y en aura deux. Ici, les nombres de Ramsey s'appliquent à deux couleurs. Avec k couleurs, il s'agit des nombres de Ramsey généralisés: R(m, n, p, q ...).	Avec six sommets (R6), il est possible de créer deux triangles (R3) distincts et de couleurs différentes.

Table des nombres de Ramsey

haut

Table des R(m, n): valeur connue ou fourchette de valeurs (cas deux couleurs)

Rappel (inutile de remplir toute la table, une moitié suffit)

R(m, n ) = R(n, m)

	1	2	3	4	5	6	7	8	9	10
1	1
2	1	2
3	1	3	6
4	1	4	9	18
5	1	5	14	25	43-48*
6	1	6	18	36-40	58-85	102-161
7	1	7	23	49-58	80-133	115-273	205-497
8	1	8	28	59-79	101-194	134-427	219-840	282-1532
9	1	9	36	73-106	133-282	183-656	252-1379	329-2683	565-6588
10	1	10	40-42	92-136	149-381	204-949	292-2134	343-4432	581-12677	798-23556
11	1	11	46-51	93-191
12	1	12	51-60	97-238
13	1	13	60-69	112-291
14	1	14	66-78	119-349
15	1	15	73-89	123-417

En ocre, valeurs qui datent de 1994 >>>

Les autres valeurs sont classiquement données, notamment sur Wikipedia

et OEIS A212954 et ses suites associées.

* On trouve généralement 49, mais un auteur (?) donne 48.

Généralisé (trois couleurs)

R(3, 3, 3) = 17 >>>

51 ≤ R(3, 3, 3, 3) ≤ 62 >>>

R(7, 7, 7) = 25 – Ralph Faudree – 2001

Une formule

R(C_n, K₄) = 3(n – 1) + 1 pour n ≥ 4 >>>

Théorème de Van der Waerden

Si on colorie les entiers naturels en r couleurs, alors il existe des progressions arithmétiques monochromes arbitrairement grandes.

D'autres valeurs en Ramsey Numbers

Historique	haut
Dates et auteurs des découvertes

Source: Ramsey's theory: two colours – Veselin Jungic

Haut de page (ou double-clic)

Retour	Ramsey: EN BREF – Tour d'horizon
Suite	Ramsey: Propriétés et calculs
Voir	Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ	Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ
Sites	Voir Références en page d'introduction
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/Valeurs.htm