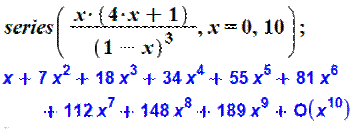|
Édition du: 18/06/2020 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||
![]()
|
7-gonal Nombres
construits en déposant des points sur des heptagones gigognes, chacun appuyé sur le précédent. |
||
|
|
Sommaire de cette page >>> Nombres heptagonaux >>> Nombres heptagonaux – Tables >>> Propriétés avec les nombres entiers >>> Propriétés avec les nombres triangulaires >>> Propriétés entre heptagonaux >>> Nombres heptagonaux généralisés >>> Langue |
Débutants Nombres
figurés ou
géométriques Glossaire |
|
Construction des nombres
heptagonaux
|
|
||
|
Notation et formules La formule en somme
résulte du décompte vu ci-dessus. L'incrément étant égal à: |
|
||
|
Caractérisation Sorte de racine heptagonale. |
Si
n est un nombre entier alors x est le énième nombre hexagonal. Sinon, il n'est
pas hexagonal. N
est la racine de x = 1/2 (5n² – 3n). |
||
|
Fonction génératrice L'instruction demande le développement sur dix
termes. |
|
||
|
Programme |
|
||
|
Somme des inverses Constante calculée pour n jusqu'à 10 000: |
|
||
|
Les 100 premiers heptagonaux |
1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342,
403, 469, 540, 616, 697, 783, 874, 970, 1071, 1177, 1288, 1404, 1525, 1651,
1782, 1918, 2059, 2205, 2356, 2512, 2673, 2839, 3010, 3186, 3367, 3553, 3744,
3940, 4141, 4347, 4558, 4774, 4995, 5221, 5452, 5688, 5929, 6175, 6426, 6682,
6943, 7209, 7480, 7756, 8037, 8323, 8614, 8910, 9211, 9517, 9828, 10144,
10465, 10791, 11122, 11458, 11799, 12145, 12496, 12852, 13213, 13579, 13950,
14326, 14707, 15093, 15484, 15880, 16281, 16687, 17098, 17514, 17935, 18361,
18792, 19228, 19669, 20115, 20566, 21022, 21483, 21949, 22420, 22896, 23377,
23863, 24354, 24850 |
|
|
Heptagonaux carrés Ces nombres sont aussi octogonaux centrés. |
1, 81,
5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025,
25635978392186449, 9976444135331412025, 729252434211108535809,
53306479301521270428241, 20744638830126197732344369,
1516379800105728357531817761, 110843467413344235941816109721 |
|
|
Heptagonaux cubes jusqu'à n = 106 |
Aucun. |
|
|
Heptagonaux et triangulaires Ces nombres sont trouvés en résolvant l'équation de Pell: X² – 5Y² = 4 Quelques solutions pour (X, Y): (3, 1), 7, 5),
(17, 13), (53,41), (133, 103), … Soit pour (n, m): (1, 1), (5, 10), (221, 493),
(1513, 3382), … Voir Brève de
Maths 522 |
Ce sont
les heptagonaux d'indices: 1, 5,
221, 1513, 71065, 487085, 22882613, 156839761, 7368130225, ... Ils sont
tels que: 1/2 n (5n – 3) = 1/2 m (m +
1). Recherche de la solution
|
||||||||||||||||
|
Heptagonaux et pentagonaux Ces nombres sont trouvés en résolvant l'équation
de Pell: 3X² – 5Y² = 22 Quelques solutions pour (X, Y): (3, 1), 7, 5),
(17, 13), (53,41), (133, 103), … Soit pour (n, m): (1, 1), (42, 54), (2585,
3337),( 160210, 206830), (9930417, 12820113), … |
Ce sont
les heptagonaux d'indices: 1, 42,
2585, 160210, 9930417, 615525626, 38152658377, 2364849293730, … Ils sont
tels que: 1/2 n (5n – 3) = 1/2 m (3m –
1). Recherche de la solution
|
||||||||||||||||
|
Heptagonaux et hexagonaux Ces nombres sont trouvés en résolvant l'équation
de Pell: X² – 5Y² = 4 Quelques solutions pour (X, Y): (3, 1), (7, 3),
(18, 8), 47, 21), 123, 55), … Soit pour (n, m): (221, 247), 71065, 79453),
(22882613, 25583539), … |
Ce sont
les heptagonaux d'indices: 1, 221,
71065, 22882613, 7368130225, 2372515049741, … Ils sont
tels que: 1/2 n (5n – 3) = m (2m – 1). Recherche de la solution
|
Voir Multi-polygonaux
|
Parité |
Cycle:
impair-Impair- pair-pair. |
|
|
Relation avec le 7 Les nombres heptagonaux, multipliés par 40
auxquels on ajoute 9, forment la liste des carrés de tous les nombres
terminés par 7, les nombres en 10n – 3. La démonstration est immédiate en développant
l'expression |
(40/2) n (5n – 3) + 9 = 100n² – 60 + 9 = (10n – 3)² |
|
trg
Pascal ?
|
P7,n = 5Tn-1 + n (Illustration) = 5/2 (n – 1)n + n = 1/2 (5n² – 5n + 2n) = 1/2 (5n² – 3n) 5 P7,n + 1 = T5n – 2 = 5/2 (5n² – 3n) + 1 = 1/2 [ 25n² – 15n + 2) = 1/2 (5n – 2) (5n – 1) = 1/2 N (N – 1) avec N = 5n – 2 P7,n
= 2Tn + 2Tn-1 + 2Tn-2 – 1 (Illustration) = 1/2 [2n(n+1) + 2n(n–1) = 1/2 [2n² + 2n + 2n² – 2n = 1/2 (5n² – 3n) |
|
|
|
Partitions d'un heptagonal en somme d'heptagonaux |
Exemple: k, 5k+1, n, He(5k+1),
He(n+1), He(n), différence 1, 6, 16, 81, 697, 616, 81 => He(17) –
He(16 ) = H(6) 2, 11, 57, 286, 8323, 8037, 286 3, 16, 123, 616, 38254, 37638, 616 4, 21, 214, 1071, 115240, 114169, 1071 5, 26, 330, 1651, 273406, 271755, 1651
Exemple: k, 25k+1,n, He(25k+1), He(n+1), He(n), différence 1, 26, 330, 1651, 273406, 271755, 1651 2, 51, 1285, 6426, 4132561, 4126135, 6426 3, 76, 2865, 14326, 20530591, 20516265, 14326 4, 101, 5070, 25351, 64279996, 64254645, 25351 5, 126, 7900, 39501, 156052651, 156013150, 39501 |
|
|
Heptagonaux du deuxième ordre |
Même
formule que pour les ordinaires avec signe plus. |
|
|
Les premiers heptagonaux du 2e
ordre |
4, 13, 27, 46, 70, 99, 133, 172, 216, 265, 319, 378,
442, 511, 585, 664, 748, 837, 931, 1030, 1134, 1243, 1357, 1476, 1600, |
|
|
Heptagonaux généralisés |
Soit la réunion des nombres heptagonaux
ordinaires avec les centrés.
|
|
|
Les premiers heptagonaux
généralisés (ordinaires et du 2e ordre) |
0, 1, 4, 7, 13, 18, 27, 34, 46, 55, 70, 81, 99, 112,
133, 148, 172, 189, 216, 235, 265, 286, 319, 342, 378, 403, 442, 469, 511,
540, 585, 616, 664, 697, 748, 783, 837, 874, 931, 970, 1030, 1071, 1134,
1177, 1243, 1288, 1357, 1404, 1476, 1525, 1600, |
|
|
Anglais: A heptagonal number is a figurate
number. Allemand:
Heptagonalzahl oder Siebeneckszahl. Espagnol: Un número
heptagonal es un número figurado. Italien: Un numero ettagonale è un numero
poligonale. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |