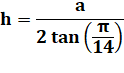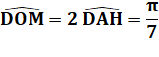|
|||||||||||||||||||||||||||||||||||||
![]()
|
HEPTAGONE régulier L'heptagone
régulier est le plus petit polygone
régulier non constructible à la règle
et au compas. Problème impossible, tout comme la quadrature
du cercle. Cependant, il existe d'autres façons de construire
l'heptagone. Vous trouverez amusant, également, de découvrir le propriétés
des diagonales de
l'heptagone. Heptagone: du grec hepta, sept, et gônia, angle. Polygone qui a
sept angles, et donc sept côtés. Anglais: heptagon |
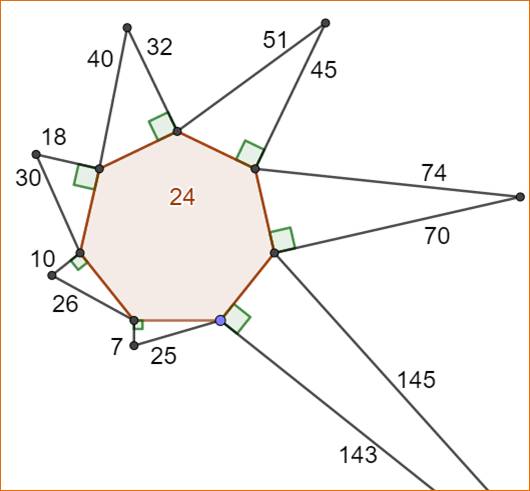
Un heptagone de côté 24
et tous les triangles rectangles
tels que a² + b² = c² en nombres entiers
(triplets)
Construction rapide
|
Microsoft
Powerpoint 2007 offre la possibilité de dessiner un heptagone régulier
facilement. Cette possibilité n'existe pas dans Word. Rappel: pour obtenir un
polygone régulier, maintenez la touche majuscule enfoncée; et pour le centrer,
maintenez aussi la touche contrôle enfoncée. |
|
|
|
||||
|
|
|
|||
|
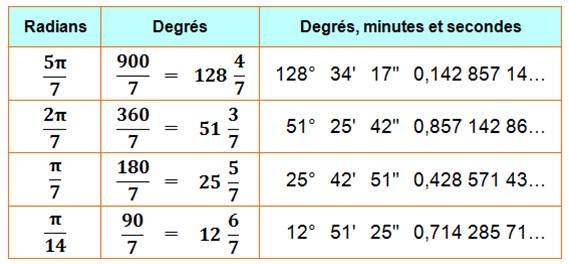
Voir Trigonométrie des
angles en Pi/7 Les
angles en Pi / 7
Note sur le symbole pour le côté:
"a" est classique, "c" est parfois utilisé pour ne pas
confondre avec l'apothème; en
anglais, c'est "s" pour side.
Évaluation
de l'écart:
L'angle Pi/3 = 60° est l'angle du
triangle équilatéral. Ce qui suggère une méthode de
construction approximative à la règle et au compas. Une
autre méthode de construction approximative (plus compliquée!) repose sur le
fait que la tangente est proche de 5/4 (Dixon en 1991):
|
||||
Voir
DicoNombre
0,86… / DicoNombre
1, 2539…
|
|
|||||||||
|
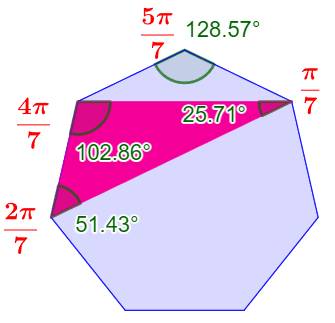
Longueur
de la diagonale k, avec k la quantité de côtés interceptés par la diagonale. |
|
||||||||
|
|
||||||||
Voir Son calcul / Tables
Les mensurations de l'heptagone

Voir Diagonales de l'heptagone –
Calculs et propriétés
|
|
||
|
|
|
|
|
|
||
|
Rayon du cercle circonscrit (extérieur)
Rayon du cercle inscrit (intérieur)
|
Notations
Aire de l'heptagone Aire triangle ODE: ½ DE x OH
Aire de l'heptagone: 7 fois
aire ODE.
|
|
|
|
|
|
|
|
|
|
Avec
un rapporteur
Tracez
un cercle de rayon voulu
|
|
|
|
|
|
Par
contre, on est sûr que François
Viète (1540-1603) a découvert cette construction par lui-même et sans le
bénéfice de l'algèbre moderne.
|
|
|
|
||
|
Principe
Rappel du calcul de la hauteur du triangle équilatéral |
||
|
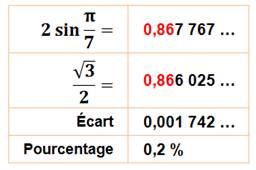
Triangle équilatéral AOC de côté R. Sa hauteur h, calculée avec le théorème de Pythagore:
Ici nous avons placé un côté du triangle
sur un rayon du cercle. |
Longueur
CE = h:
Différence:
0,0017… soit
de l'ordre de 2 pour mille. |
|
|
Construction de l'heptagone dans un cercle donné Pour
construire l'heptagone régulier, facile! 1) Cercle de diamètre AOB; 2) Médiatrice CED de AO;
et 3) La mesure du segment CE est
très proche de celle du côté de l'heptagone. Ouvrir le compas sur cette
mesure CE et la reporter six fois sur le cercle.
Notez qu'en commençant avec un cercle de rayon CE et de
centre A, le report six fois de ce cercle nous amène en F qui est quasiment à
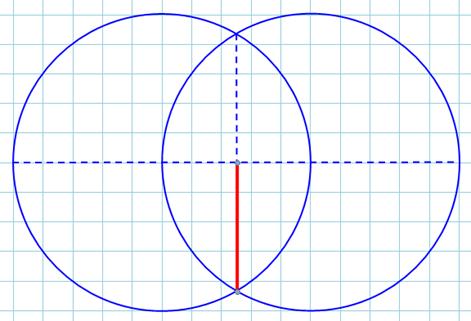
l'intersection du cercle initial (bleu) et du premier cercle dessiné en A. Tracé alternatif (simple) Deux
cercles de rayon unité comme montré sur la figure. La
longueur du segment rouge (
Autre présentation (équivalente, mais moins facile à
dessiner)
1) Dessinez un triangle équilatéral dans un
cercle; et 2) Reportez AH sur le cercle, mesure proche
de celle du côté de l'heptagone. |
||
Merci à Jean-Paul D.
pour sa contribution
|
|
||
|
Les constructions précédentes approchaient le côté de l'heptagone à 2
pour 1000. La présente construction va réussir 7 pour 10 000. Construction Le
cercle contenant l'heptagone et son carré circonscrit ABCD. Le
triangle équilatéral AEB s'appuyant sur AB. M
et N intersection du triangle avec le cercle. QM
est la longueur du côté de l'heptagone à un iota près.
Calcul de la longueur QM Système
d'axes avec A pour origine |
||
|
Dans
le triangle rectangle:
AEQ avec Pythagore: |
AQ = R = 1 (rayon du cercle
bleu) QE² = AE² – AQ² |
|
|
Équation
de la droite AE -
origine des axes en A -
Pente = coefficient directeur |
|
|
|
Équation
du cercle de centre O(1, 1) |
(x – 1)² + (y – 1)² = 1 |
|
|
-
En remplaçant y par sa valeur en
fonction de x pour la droite |
(x – 1)² + ( |
|
|
On
obtient une équation quadratique en x |
x² – 2x + 1 + 3x² – 2 4x² – 2(1 + 4x² – 5,4641… x +1 = 0 |
|
|
Solutions – Discriminant |
D = b² – 4ac = (-2(1 + = 4 (1 + =13,8564…
|
|
|
Racine
en x (Celle
qui nous intéresse. Plus bas, les deux solutions) |
|
|
|
Racine
en y |
y = |
|
|
Coordonnées des sommets
du triangle rectangle MPQ et
comparaison à la longueur réelle du côté du pentagone (avant-dernière ligne):
|
||
Merci à Jérôme Bial de Bellerade pour ses
remarques
Pour information
|
Les deux solutions analytiques
(avec radicaux):
Rappel: puissance ¼ veut dire racine
quatrième de 3, soit la racine de la racine. Les valeurs
numériques:
|
|
|
|||
|
Une
idée de la démonstration |
|||
|
|
z7 |
= 1 |
|
|
|
z |
= 1 |
|
|
|
(z7 – 1) |
= (z – 1) . f(z) |
|
|
|
(z7 – 1)
/ (z – 1) |
= z6 + z5 + z4 + z3
+ z2 + z + 1 |
|
|
|
z |
= cos(360/7) + i . sin(360/7) |
|
|
|
x |
=
z + 1/z |
|
|
|
0 |
=
x3 + x2 – 2x - 1 |
|
|
|
x |
=
p/q |
|
|
|
q3 |
=
p (p2 + pq – 2q2) |
|
|
|
p3 |
=
q (q2 – p2 + 2pq) |
|
|
|
p |
=
|
|
|
Voir Trisection |
q |
=
|
|
|
Ce
qui est impossible
|
|||
|
|
|
|
A heptagon is a seven-sided
polygon. The name septagon is not recommended. The regular heptagon is not a
constructible polygon. Just as Archimedes
described a method for trisecting an angle using a pair of compasses and a
straight edge with two marks on it, so he gave a most ingenious method for
constructing a regular heptagon. A heptagram or septagram is a
seven-pointed star drawn with seven straight strokes. There are two kinds of
heptagram: obtuse or acute:
Each of the seven days of the week are represented as follows
(clockwise):
|
|
|
Polyèdre à sept
faces. Aucun n'est régulier. Une maison simple avec quatre murs un toit à
deux pans et un sol est un heptaèdre. L'heptaèdre de Szilassi est particulier. Chaque face a une
arête commune avec les six autres faces. Il présente des similitudes avec le tore:
surface homéomorphe. |
![]()
|
Suite INDEX |
|
|
|
Voir |
|
|
|
DicoNombre |
||
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Histoire/Heptagon.htm |
|
![]()