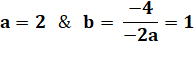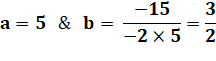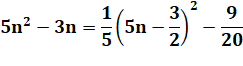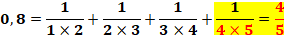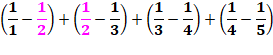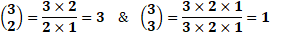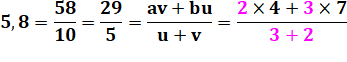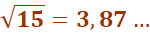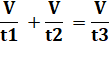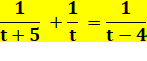NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 27

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

520. Année 2020 et palindromes
Cette date constitue un palindrome en l'écrivant à l'européenne comme à l'américaine. Rare. Certains chercherons le raffinement avec le 2 février 2020 à 02 h 02 minutes 20 secondes et 20 centièmes: 02 02 2020 02 02 20 20
Extraordinaire, du fait que 2020 est bissextile: le 2 février est le 33^e jour de l'année et il reste 333 jours pour finir l'année.
Brèves associées	>>> Palindromes		>>> Nombres pannumériques
Pour en savoir plus	>>> Dates palindromes		>>> Années bissextiles

521. Journée internationale des Maths
C'est le 14 mars, car, chez les Américains on écrit la date comme ceci: 3/14, ce qui rappelle le fameux nombre Pi = 3,14159 … L'IDM (International Day of Mathematics) a été fixé par l'UNESCO en novembre 2019. Il y a plus de trente ans, c'est Larry Shaw, physicien américain qui a associé cette date à la constante Pi. Note: Albert Einstein est né le 14 mars 1879 à Ulm. Le 14 mars 2018 mourrait Stephen Hawking.		Many mathematicians throughout history have tried to move beyond mere approximation in an effort to nail down the exact numeric equivalence of pi, but the solution remains a mystery. De nombreux mathématiciens au cours de l'histoire ont tenté de dépasser la simple approximation dans le but de déterminer l'équivalence numérique exacte de pi, mais la solution reste un mystère.
Brèves associées	>>> Actualités 2018	>>> Mnémotechnique des chiffres
Pour en savoir plus	>>> Constante Pi >>> Einstein >>> Hawking / Trous noirs	>>> Actualités 2020 >>> Bagage anglais indispensable pour le bac et pour le business

522. Carré tronqué à restituer
Comment obtenir un carré à partir d'un développement tronqué. Les exemples aideront à comprendre la manière de s'y prendre. Cas où a est un carré 4m² – 4m = ? 4m² – 4m + b² = (ax – b)² = ax² – 2axb + b² 4m² – 4m = (2m – 1)² – 1		Cas où a n'est pas un carré 5n² – 3n = ? 25n² – 15n + b² = (ax – b)² = ax² – 2axb + b²
Brèves associées	>>> Carré = cube		>>> Brèves de maths – Index
Pour en savoir plus	>>> Identités remarquables		>>> Nombres heptagonaux (application)

523. Nombres consécutifs
Théorème La somme de plus de deux nombres consécutifs n'est jamais un nombre premier. Si k, la quantité de nombres, est impaire, la somme est divisible par k. Ex avec k = 3: 12 + 13 + 14 = 39 = 3 x 13 Si k est pair, la somme est divisible par k/2. Ex avec k = 6: 2+3+4+5+6+7 = 27 = 3 x 9		Démonstration La somme de k nombres à partir de n est égale k fois le nombre n et des suppléments qui représentent la somme de k nombres entiers: Ex: 10 + 11 + 12 + 13 = 4 x 10 + (0 + 1 + 2 + 3) = 46 Formellement: Si k est impair, k-1 est pair est (k-1)/2 est un entier (a). Si k est pair, k/2 est un entier (b). Dans les deux cas, la somme est le produit de deux facteurs, il est composé à condition que k > 2.
Brèves associées	>>> Produit de nombres consécutifs		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Somme de nombres consécutifs		>>> Nombre composé

524. Somme de produits d'inverses
Propriété La somme des inverses des produits de deux nombres consécutifs est simplement égale au nombre divisé par son successeur. Exemple pour n = 4 Astuce du procédé par télescopage Avec l'exemple numérique Chaque terme négatif est annulé par le terme suivant. Phénomène de cascade.
Brèves associées	>>> Somme des entiers >>> Somme de fractions – Calcul		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Somme des inverses des nombres triangulaires			>>> PGCD >>> Nombre 0,8

525. FORT BOYARD – Septembre 2020

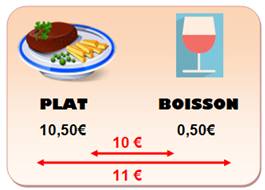
Devinette

Dans ce restaurant, plat et boisson coûtent 11€.

Le plat coûte 10 euros de plus que la boisson.

Combien coûte la boisson: 0,50€, 1€ ou 2€.

Réponse faite durant le jeu

C'est 1 €. La candidate a reçu des litres de liquide slime* sur la tête, synonyme de mauvaise réponse.

*Pâte gluante et élastique

Piège

Ce qui est d'un côté, l'est le l'autre.

Ce qui est plus, l'est en moins.

Il faut partager le 1 euro en deux.

La réponse est 0,50 euro.

Pas convaincu !

Pourtant avec Boisson = 0,50 et Plat = 10,50, on a bien une différence de 10 et un total de 11.

Illustration

Petite équation pour confirmation

Coût total:	P + B	= 11
Comparaison:	P	= B + 10
On ajoute les deux:	2P + B	= B + 21
Soustraction de B: Division par 2:	2P P	= 21 = 10,5

Brèves associées

>>> Classique énigme des 30 euros

>>> Brèves Énigmes – Index

Pour en savoir plus

>>> Cette devinette et d'autres

>>> Équation – Débutants

526. Pile ou face
Énigme Vous lancez une pièce de 1 euro trois fois. Quelle est la probabilité de tomber sur deux faces, au moins ? If you flip a coin 3 times, what is the probability of flipping at least 2 Heads ? Observations Certains vont dire qu'à chaque jet, on a 1 chance sur 2 d'avoir face (comme d'avoir pile). Pour en avoir 2, il suffit que deux jets soient bons. J'ajoute les chances: 1/2 + 1/2 = 1/4 = 25%. Ce n'est pas la bonne réponse ! Beaucoup imagine malgré tout que c'est moins de 50%. Réponse Le mieux pour s'en convaincre est de recenser les possibilités. L'illustration monte qu'il y a 8 cas possibles et, en rouge, 4 cas avec au moins 2 faces; le dernier en comportant 3. Ce dernier cas est inattendu. Il ne faut pas l'oublier. Dénombrement Supposons que nous lancions 3 pièces en une fois, ce qui revient au même que 3 lancers successifs. Nous sommes dans le cas d'une combinaison de 2 parmi 3 à ajouter à une combinaison de 3 parmi 3. La somme vaut 3 + 1 = 4 La totalité des cas est 2^3 = 8 (2 cas avec la première, et pour chaque cas, 2 cas pour la deuxième, puis encore à chaque cas, 2 cas pour la troisième: 2 x 2 x 2 = 8 Probabilité = cas favorables / tous les cas = 4/8 = 1/2 = 50%			Cas possibles lors du lancer de trois pièces Huit combinaisons dont 3 avec deux faces et 1 avec 3 faces. Total: 4 sur 8 = 50%
Brèves associées	>>> Jeu de dés	>>> Brèves Compter – Index
Pour en savoir plus	>>> Pile ou face	>>> Probabilités >>> Combinaisons

527. Diagonales de l'octogone
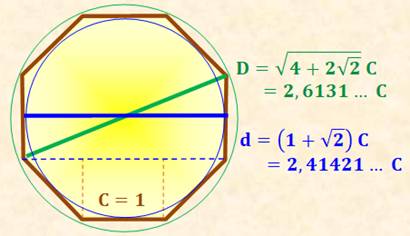
TROIS CONSTANTES Dans le cercle, PI Dans le pentagone, le nombre d'or Dans l'octogone, le nombre d'argent (diamètre du cercle inscrit)
Brèves associées	>>> Octogone >>> Diagonales des polygones		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Octogone – Développements >>> Nombre d'argent		>>> Constante Pi >>> Nombre d'or

528. Construire une fraction
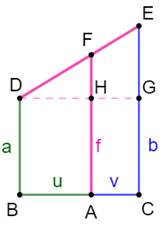
Formulation Dans le triangle DGE, application du théorème de Thalès: Application On se propose de construire une longueur égale à 5,8. Le dénominateur est choisi pour faire u + v, sachant que u et v sont les multiplicateurs de deux nombres au numérateur.
Brèves associées	>>> Somme de fractions		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Construire une fraction		>>> Construction élémentaires >>> Fractions

529. Motifs avec retournement

Motif: n + k = R(n x k)

Nombre qui multiplié par k et retourné donne le même nombre qu'en ajoutant k.

Avec k = 2, 5 ou 15, on obtient des motifs itératifs. Seul cas sans 0, avec k = 2.

Avec k = 4, 6, 7, 10, 12, 13, 14,15, 16, 17, 19, 20 … pas de motif du tout.

Un motif itératif

k = 2	+	x
47	49	94
497	499	994
4997	4999	9994
49…97	49…99	9…994

k = 5	+	x
26	31	130
386	391	1930
3986	3991	199930
39…986	39…91	19…9930

Plusieurs motifs itératifs

k = 15	+	x
228	243	3420
624	639	9360
2568	2583	38520
25968	25983	389520
216408	216423	3246120
259968	259983	3899520
2160408	2160423	32406120
2599968	2599983	38999520
6081204	6081219	91218060

Un seul motif

k = 3	24	27	72
k = 8	455	463	3640
k = 9	9	18	81
k = 11	110	121	1210
k = 18	17595	17613	316710
k = 21	600	621	12600

Brèves associées

>>> Motif itératif en 98 et 99

>>> Brèves Motifs – Index

Pour en savoir plus

>>> Motifs – Index

>>> Nombres retournés

530. Racine de n – Construction
Tout nombre est somme de quatre carrés. Prenons le nombre 15: 15 = 1² + 1² + 2² + 3² = a² + b² + c² + d² = u² + v² avec u² = a² + b² et v² = c² + d². Construction Disposer les quatre nombres (a, b, c et d) sur les axes comme indiqué. Reporter les longueurs des diagonales bleues (u et v) sur les axes (arcs verts). Le segment (rose) qui joint les intersections avec les axes est la racine de n (ici n = 15) Justification
Brèves associées	>>> Construction dorée remarquable		>>> Brèves Construction – Index
Pour en savoir plus	>>> Construction de racine de n		>>> Somme de quatre carrés

531. Les trois tuyaux - Énigme
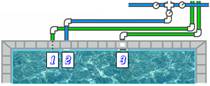
Problème On dispose de trois tuyaux de débit constant pour remplir la piscine. Avec les deux premiers, utilisés simultanément, il faut le même temps que pour la remplir avec le 3^e seul. Le 2^e tuyau la remplit en 5 heures de moins que le premier et en 4 heures de plus que le 3^e. Quelle est la durée de remplissage pour chaque tuyau seul ?			Relations t = t2 = 10 heures t1 = 15 h et t3 = 6 h.
Brèves associées	>>> Pesée des neuf billes	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Les trois tuyaux – Explications	>>> Transvasements – Énigmes

532. Grille 8x8 et 3 points
Sur une grille de 8 x 8 points, disposés régulièrement, on souhaite dessiner les droites qui passent par trois points, mais uniquement trois points. Le dénombrement n'est pas simple, mais il se trouve qu'il y a exactement 100 telles droites.
Brèves associées	>>> Droites dans le triangle		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Grilles et droites par 3 points		>>> Nombre 100

533. Nombres premiers et 30
On note n# la primorielle de n, qui est le produit des nombres premiers inférieurs à n ou égal à n. Tous les nombres plus grands que n# sont évidemment de la forme n#. k + i pour i prenant toutes les valeurs inférieures à n#. Certaines valeurs de i conduisent à des nombres composés facilement reconnaissables.		Avec 6#, par exemple, on a 6# = 2 x 3 x 5 = 30. Or, tout nombre est de la forme 30k + i avec i = {0, 1, 2, 3…, 29}. Tous ceux avec i divisible par 2, 3 ou 5 sont composés. Pour qu'un nombre soit premier, il ne reste que i = {1, 7, 11, 13, 17, 19, 23, 29}. Ce sont d'ailleurs les nombres i tels que PGCD (1, 30) = 1; autrement dit: i est premier avec 30. Bilan: tous les nombres premiers sont de la forme 30k + i avec i = {1, 7, 11, 13, 17, 19, 23, 29}. Mais tous les nombres de cette forme ne sont pas premiers.
Brèves associées	>>> Premiers en 6k+1 et 6k+5		>>> Brèves Premiers – Index
Pour en savoir plus	>>> Premiers et nombre 30		>>> Primorielles >>> PGCD

534. Somme de carrés en PA
Comment calculer la somme suivante d'une manière générale ? S = 5² + 11² + 17² + 23² = 964 Somme de carrés en progression arithmétique (PA). Notations et exemple Le premier terme: F = 5 (comme First) Le dernier: L = 23 = F + (n – 1) r La quantité de termes: n = 4 La raison de la progression: r = 6		Formule Calcul numérique L = F + (n – 1) r = 5 + 3x6 = 23 S = 5 x 23 x 4 + 1/6 (3x4x7) x 6² S = 460 + 504 = 964
Brèves associées	>>> Nombres somme de carrés		>>> Brèves Suites – Index
Pour en savoir plus	>>> Sommes des carrés		>>> Progression arithmétique

535. Somme des cubes en PA
Comment calculer la somme suivante d'une manière générale ? S = 5^3 + 11^3 + 17^3 + 23^3 = 18 536 Somme de cubes en progression arithmétique (PA). Exemple F = 5 L = 23 = F + (n-1) r n = 4 r = 6		Formule Calcul numérique L = F + (n – 1) r = 5 + 3x6 = 23 T = 1/2 4 (5+23) = 56 S = 6 x 56² + 56 x 5 x (5 – 6) S = 18 816 – 280 = 18 536
Brèves associées	>>> Calcul mental du cube		>>> Brèves Premiers – Index
Pour en savoir plus	>>> Sommes de cubes		>>> Progression arithmétique

536. Divisibilité par 137
Divisibilité par 11 On connait le procédé pour tester si un nombre est divisible par 11. La somme alternée des chiffres doit être divisible par 11 (nulle). Exemples 121 => 1 – 2 + 1 = 0 135 795 => 1 – 3 + 5 – 7 + 9 – 5 = 0 244 442 => 2 – 4 + 4 – 4 + 4 – 2 = 0 Généralisation On généralise à d'autres cas, en prenant des tranches de 2, 3, 4 … chiffres. C'est le cas pour 137 avec des tranches de quatre chiffres.		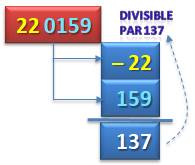Divisibilité par 137 Pour 137, comme pour 73, on sépare le nombre en tranches de quatre chiffres. La somme alternée doit être divisible par 137. Exemples
Brèves associées	>>> Divisibilité par 11 – Dominos		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Divisibilité – Méthode par tranches		>>> Divisibilité par n

537. Nombre 12345679

Ce nombre (tous les chiffres sauf 8) est le nombre de Lewis Carroll.

Il divise les nombres ayant neuf chiffres répétés (repdigits).

On le retrouve dans la division par 81:

1	× 9	× 12 345 679	= 111 111 111
2	9	12 345 679	222 222 222
3	9	12 345 679	333 333 333
4	9	12 345 679	444 444 444
5	9	12 345 679	555 555 555
6	9	12 345 679	666 666 666
7	9	12 345 679	777 777 777
8	9	12 345 679	888 888 888
9	9	12 345 679	999 999 999

Brèves associées

>>> Nombre 0,142857 … = 1/7

>>> Brèves Nombres – Index

Pour en savoir plus

>>> Nombre de Carroll

>>> Pépites numériques

>>> Repdigit

>>> Pannumérique (tous les chiffres)

538. Puzzle du Quatre 4
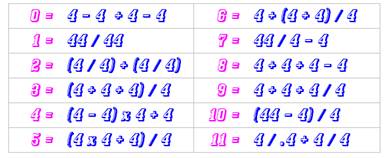
Principe Ce puzzle est assez ancien et a fait réfléchir beaucoup de monde. Écrire un maximum de nombres successifs en utilisant seulement quatre fois le chiffre 4.			Les onze premiers nombres
Cas du nombre 100
Brèves associées	>>> Opérations mystérieuses			>>> Brèves Jeux – Index
Pour en savoir plus	>>> Jeu du Quatre 4			>>> Nombre 4

539. Nombre 42
Le nombre décimal 42 s'écrit avec un "10" répété trois fois en binaire. Autrement-dit: il est la somme des premières puissances impaires de 2 et le double des premières puissances de 4. Les nombres en 1010 … en binaire (10 répété k fois) sont accessibles par la formule indiquée. Dans un roman, le nombre 42 est la réponse de l'ordinateur qui ne connait pas la réponse à la question sur la vie … >>>		Nombres en 1010 … binaire ou 222 … en base 4 Formule pour tous ces nombres (k répétitions) Liste de ces nombres 0, 2, 10, 42, 170, 682, 2730, 10922, 43690, …
Brèves associées	>>> Nombre 13		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 42 insolite		>>> Nombre 42

Retour	Brèves de maths – Page 26
Suite	Brèves de maths – Page 28
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve27.htm