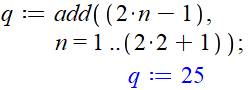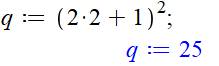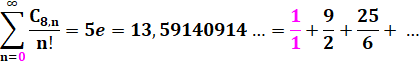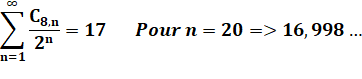|
Édition du: 17/02/2025 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||
![]()
|
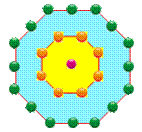
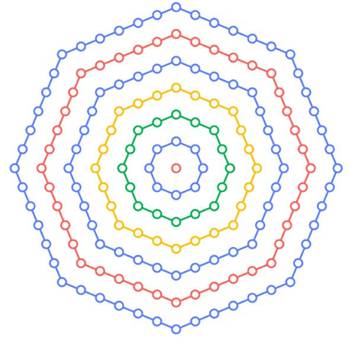
8-gonal centrés Nombres
construits en déposant des points sur des octogones
concentriques. |
||
|
|
Sommaire de cette page >>> Caractéristiques >>> illustration >>> Liste |
Débutants Nombres
figurés ou
géométriques Glossaire |
|
|
|||||
|
Famille |
|
||||
|
Définitions |
NOMBRE OCTOGONAL CENTRÉ ou carré des nombres
impairs Nombre formé à partir d'un point central et d'octogones concentriques. |
||||
|
Dénombrement |
Le nombre octogonal centré de rang n est la est la somme des
premiers nombres impairs. C'est un nombre carré. |
|
|
||
|
Sommes |
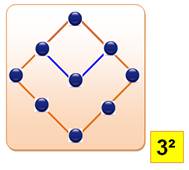
Si m est
la quantité de couches avec plus de 1 point (m = n – 1 = 3 – 1 = 2) Sur les
figures, la quantité de lignes (à gauche) ou de carrés (à droite) est: |
||||
|
|
|
|
|||
|
|
Somme des
nombres impairs Exemple
|
Carré de
la quantité de couches Exemple
Note: Rien d'exceptionnel, car on sait que la somme des
impairs est un carré. |
|||
|
Formule |
n > 0 C8,n = 4n (n – 1) + 1 C8,n = 8 Tn-1 + 1 T n-1
étant le nombre triangulaire
d'ordre n – 1 |
|
|
Propriétés |
Ils
sont tous impairs et les unités forment le cycle: {1, 9, 5, 9, 1} La
fonction tau* de Ramanujan des
nombres octogonaux centrés est égale à un nombre impair; elle est paire pour
tous les autres nombres. * fonction
de mathématique avancée. |
|
|
Relations |
|
|
|
Anglais |
Centered
octagonal number |
|
|
||
|
Nombres
octogonaux centrés Chaque
nombre octogonal centré d'ordre n est
le cumul des points sur l'octogone de côté n et de tous les cercles
intérieurs. C8,4
= 24 + 16 + 8 + 1 = 49 = 7² C8,5
= 49 + 32 = 81 (illustration) Par
la formule C8,5
= (2n – 1)² = (2 × 5 – 1)² =
9² = 81 En
dénombrant 1 + 8(1 +
2 + 3 + 4) = 1 + 8 ×
10 = 81 |
|
|
|
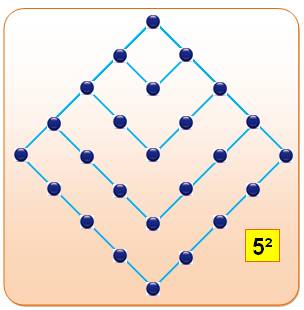
C8,6
= (2n – 1)² = (2 × 6 – 1)² =
11² = 121 C8,7
= (2n – 1)² = (2 × 7 – 1)² = 13² = 169 (illustration) |
|
|
|
C8,23
= (2n – 1)² = (2 × 23 – 1)² = 13² = 2025 (illustration) Quantité
de points par couche: Après le
nombre 1, ce sont tous les multiples de 8
jusqu'à 22. Le dernier étant: 22 × 8 = 176. |
|
|
![]()
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()