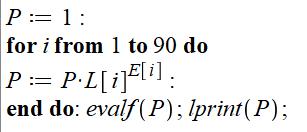|
||||||||||||||||||||||||||||
![]()
|
Nombres ORDINAIRES & Nombres EXTRAORDINAIRES
Caractérisation d'un nombre
par rapport à sa quantité
de diviseurs. On cherche le nombre le plus
petit ayant une quantité donnée de
diviseurs (tau). La méthode est simple, mais elle présente des ratées. Dans
le premier cas les nombres sont ordinaires, dans le deuxième, ils sont extraordinaires. Voyons d'abord comment
trouver un nombre N connaissant sa quantité de diviseurs. |
|
ayant
une quantité donnée de diviseurs |
|
|
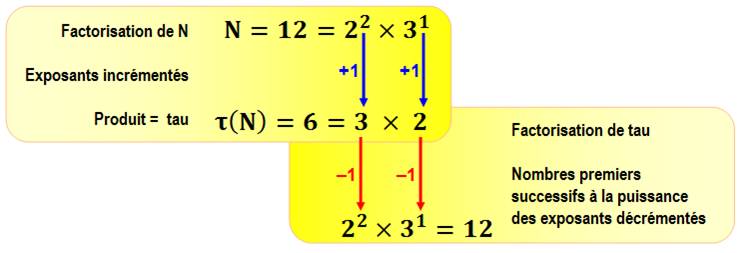
Comment passer de N puis à la quantité de
diviseurs (tau) puis retour à N? On rappelle que tau
est égal aux produits des exposants de la factorisation première du
nombre, chaque exposant étant augmenté d'une unité.
Conclusion: on sait calculer
tau; il suffit d'effectuer l'opération inverse pour retrouver ce nombre. Mais
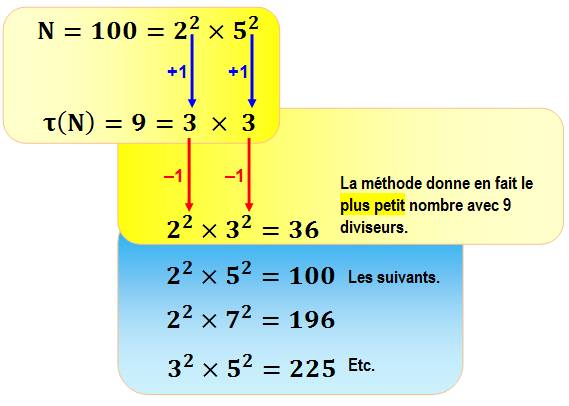
est-ce le plus petit dans tous les cas? Recherche du plus petit Le nombre reconstitué avec
la méthode indiquée semble engendrer le plus petit nombre ayant cette
quantité de diviseurs. C'est le cas avec cet exemple.
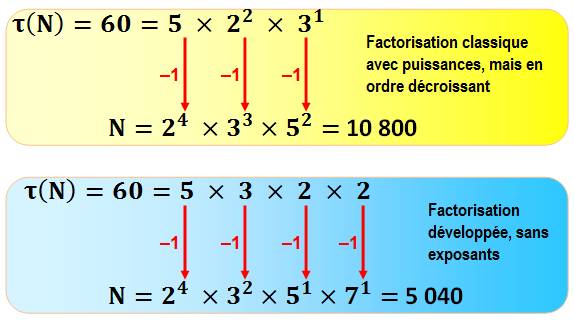
Cas de nombres plus composés: méthode un peu
corrigée
La méthode semble marcher à
condition d'ordonner les exposants dans l'odre décroissant. Cas de factorisation avec puissances: deuxième
correction
|
|
|
Méthode |
Pour obtenir le nombre généralement le plus petit pour tau donné: 1.
Factoriser le nombre tau 2.
complètement sans exposant en k facteurs 3.
en ordre décroissant 4.
former le produit des k premiers nombres premiers 5.
attribuer leur un exposant égal aux facteurs de tau décrémenté d'une
unité. |
|
Exceptions! |
La méthode fonctionne pour
une grande partie des nombres, mais présente des exceptions. Avant de conclure que le nombre
trouvé est le plus petit, il sera nécessaire de faire quelques test
complémentaire avec des factorisations voisines |
![]()
|
|
||
|
Le problème Soit un
nombre de départ. Quel est
le plus petit nombre ayant cette quantité de diviseurs (nombre ordinaire) Ayant obtenu
ce fameux nombre, quel est le nombre ayant cette quantité de diviseurs. Ainsi de
suite. Ni +
1 = plus petit nombre ayant Ni diviseurs. |
Les nombres N successifs sont des nombres ordinaires obtenus par un
procédé en cascade. |
|
|
Départ Le cas le
plus classique consiste à commencer par N1 = 3. |
|
|
|
Calcul de N2 N2
est le nombre ordinaire ayant trois diviseurs. En appliquant notre procédure:
|
On vérifique que Tau(4) = 3 avec les trois diviseurs: 1, 2 et 4. |
|
|
Calcul de N3 Application
de la procédure:
|
Vérification: Tau(6) = 4 avec les quatre diviseurs: 1, 2, 3 et 6. |
|
|
Calcul de N4 Application
de la procédure:
Notons une
progression assez lente en début de séquence; ça va changer bien vite! |
Tau(12) = 6 avec les six diviseurs: 1, 2, 3, 4, 6 et 12. |
|
Calcul de N5
On
reconnait l'intérêt des nombres 12 et 60 comme bases
de numération du fait de la quantité de leurs diviseurs. |
Tau(60) = 12 avec les six diviseurs: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20,
30 et 60. |
|
Calcul de N6
|
|
Le
nombre 5 040 a 60 diviseurs qui a 12 diviseurs qui a ….

|
Calcul de N7
N7 est un
nombre de 12 chiffres (293 milliards et
quelques) qui a bien 5 040 diviseurs. |
|
|
Calcul de N8
|
N8 = 0,6700591682 1075 = 67005 9168204585 1683714764 3892742111
2933837297 6409909041 5466796800 0000000000 |
|
Calcul de N9
|
N9
= 0,221501134 9478644095 0264049795 8923575674 4833054359 5928430876
03935781614 3046731440 6250757664 9006384094 … 101
429 (les
100 premiers chiffres sur les 1 429 chiffres de N9) = 260 x 358 x 552
… |
Merci à Jean-François A. pour l'idée de cette recherche
![]()
|
Calcul de N(9) |
|
|
N(8) est
connu (is known) =
218 x 316 x 512
x 710 x 116 x 136 x 174 x 194
x 232 x 292 x 312 x 372 x 41 x 43
x 47 x 53 x 59 x 61 Quantité de
facteurs (quantity of prime divisors):
18 + 16 + 12 + 10 + 6 + … = 90 Construction
de n(9) On prend les 90
plus petits nombres premiers (let's
take the first prime numbers) L = [2, 3, 5, 7, 11, 13,
17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97,
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173,
179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257,
263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439,
443, 449, 457, 461, 463] On prend facteurs
de N8 en ordre inverse et autant de fois que l'exposant l'indique (let's take prime factors in reverse order
and as many times as indicated by exponent) et soustraire 1 (and substract 1): E = [60, 58, 52, 46,
42, 40, 36, 36, 30, 30, 28, 28, 22, 22, 18, 18, 18, 18, 16, 16, 16, 16, 12,
12, 12, 12, 12, 12, 10, 10, 10, 10, 10, 10, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 4,
4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] On calcule
produit de chacun des nombres premiers à la puissance du bas (compute the product of each prime to the
power of the numbers in the lower list): N(9) = 2^60 x
3^58 x 5^52 x … Valeur
de n(9)
2215011349478644095026404979589235756744833054359592843087603935781614304673 1440625075766490063840943765700832191232099204099110695173019204019168007009 9258637095216350924985891323057739183410627063654466477135259366151668288687 6157361492337878294366541610149102544218991969470108442756803208895049455487 0775933390564614442061610116942471093874697753235677808371619865143138549844 1027832306547752145312092878244450226142145798559549028522861234317483570442 8952197105550866742946526392012521597790843518167928383106590805202479989824 0090656449914957441361904615173971357192444676196306797045170239382166625701 7910937451373021611291556732279489181054128530381042502638423081908981894661 7123204453294984009831330086998604006318321338856009203671703310727916959163 6945405416285878495216394798435209609485202769198882767333007285193559927062 3570365544650038632216962707023060880754074737116314797401330078656785593484 2067311369379165662857920302028228801560307113329919401124507181823727933555 1039825398746904728952945979308124651933830416677457159594884342864930304434 3690875286586154249638826866404968793590249831130410242529440582396205285129 1331490918365133613601441717535488183819522054695771472082511719055812459683 9661870371125501099411589091274870037302226370991390284596790835666704611526 7823987277299416059397573068942450864294183954028322732025122531853723815657 1598338560000000000000000000000000000000000000000000000000000 Le programme de
calcul est le suivant (the program is
as follows)
Construction
de N(10) Vous pouvez calculer N(10) à partir des facteurs
de N(9) qui se lisent: 260. 358 .552 …
Il commence par: 2462 x 3460
x 5456 x … |
|
|
N(9) est formé
selon la méthode exposée, vérifiée jusqu'à N(6). Les valeurs sont probables,
mais non prouvées au-delà de N(6). (N(9) has been
constructed according to exposed method, verified up to n(6). Beyond, values
are likely to be true, but not proved. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/Ordinair.htm
|
![]()