NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Arithmétique
Débutants Opérations	MODULAIRE				Glossaire Nombres
INDEX Théorie des nombres	Introduction	Théorie		Propriétés	Formulaire
	Applications	Calculs		Carrés	Cubes
	Jeux	Sun Zi		Mod 9, 10, 11	Carrés et Cubes
	Parité	7 ^ 7 ^ 7		Log modulaire	11^10 = 32 mod 71
	Classes de congruence		Cas de 2^33 et 2^99		Magie
	N = 1 mod k (k = 2, 3,…)		Triangle des modulos
		Sommaire de cette page >>> Je connais déjà depuis la maternelle >>> Modulo ou arithmétique de l'horloge >>> Enroulement >>> Si on ne comptait que jusqu'à 5 … >>> Exemples d'application

MODULO (congruence)

Une façon de compter qui s'intéresse aux restes.

Comme si on débitait une bille de bois en stères et que l'on s'intéressait uniquement aux chutes au-delà du mètre.

Exemple

C’est Gauss qui a inventé cette curieuse arithmétique, maintenant très utilisée en théorie des nombres.

Une opération juste est également juste dans son image modulo n.

Pour dire qu'un nombre premier, divisé par 6, donne toujours un reste de 1 ou 5, on dit simplement: P est égal à 1 ou 5 modulo 6, noté:

Devinette

Trouver le nombre qui:

divisé par 11 a un reste 4,

divisé par 15 a un reste 10, et

divisé par 19 a un reste 16.

Solution

Je connais ce domaine sans le savoir
Quand à l'école primaire vous avez fait connaissance avec les nombres pairs et impairs vous faisiez du calcul modulo 2 sans en connaître le nom. un nombre pair est un nombre égal 0 modulo 2: divisé par 2 son reste est nul. un nombre impair est un nombre égal 1 modulo 2: divisé par 2 son reste est égal à 1. Modulo est un mot qui signifie que l'on met en rang par 3, 4, … n … En fait, une généralisation des nombres pairs et impairs.	8 est pair et 8 = 0 mod 2 9 est impair et 9 = 1 mod 2

MODULO ou arithmétique de l’horloge
Imaginons un monde où n’existeraient que les nombres de 1 à 12, comme sur une horloge. Après 12, on retrouve 1, 2, 3 ... Le 12 se confond avec le 0 L’arithmétique serait particulière	On peut aussi bien dire qu'il est 14 h ou 2 h de l'après-midi. 14 modulo 12 est égal à 2.

Voir Horloge / Fractions sur l'horloge / Affichage de l'heure (algorithme)

Le signe signifie " congruence " :

1 + 3 est congru à 4 modulo 10

1 + 3 4 mod 10

1 + 3 mod 10 égal 4

On peut aussi écrire (si pas de confusion possible) :

7 + 7 = 2 mod 12, lu 2 modulo 12

Mais il est préférable de mettre le signe égal à trois barres.

7 + 7 2 mod 12

Évidemment, avec

a et m sont des entiers quelconques

Le résultat b (reste de la division de a par m) est compris entre 0 et m – 1.

Dans le monde du modulo m, on peut effectuer l’addition, la soustraction et la multiplication comme d’habitude.

Si m est premier, on peut aussi diviser par tout nombre non nul. Le calcul du résultat est un peu plus complexe.

Modulo enroulé

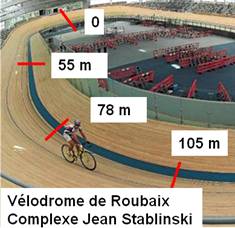
Imaginez un vélodrome avec un anneau de 250 m de long. Ce cycliste sait qu'en dix minutes il fait toujours un peu plus de vingt tours, mais il veut comparer ses records. Tous les jours, lorsque le chrono marque 10 minutes, il note de combien il dépasse: 55 m puis 78 m et aujourd'hui, c'est 105 m. Il vient de battre son record! Ce cycliste fait un calcul en modulo sans le savoir. En trigonométrie, seul l'angle sur le cercle compte. Le nombre tours que pourrait faire cet angle ne nous intéresse pas. Il peut tourner cent fois, mille fois … on s'en fiche! On dit que l'angle est connu à 2k près; on aurait pu dire: modulo 2.

Si on ne comptait que jusqu'à 5 …
Tous les nombres seraient rangés dans seulement cinq compartiments (cinq classes) Exemples d'opérations en modulo 5

Voir Preuve par 9

En pratique

Notez que toutes les calculettes scientifiques, dont celle de votre ordinateur, possèdent la touche Mod.

En bref

Voir Le nombre 763 est un nombre modeste / Division euclidienne

Exemples d'application
Théorème MOD 4 Un nombre pair porté à une puissance est égal à 0 mod 4. Un nombre impair porté à une puissance est égal à 1 ou à lui-même mod 4. Théorème MOD 3 Avec un peu d'habitude, vous pourrez prouver le résultat présenté dans le tableau. Nombres divisibles par 3 à une puissance => divisible par 3 Nombres divisibles par 3 avec reste 1 à une puissance => reste 1 si divisé par 3 Nombres divisibles par 3 avec reste 2 (équivalent à -1) à une puissance => reste 1 ou 2 si divisé par 3 selon que la puissance est paire ou impaire.	En effet: Le nombre n est pair, alors n = 2k et (2k)^h = 2^h k^h or, avec h > 1 , 2^h est toujours divisible par 4. Le nombre n est impair: n = 2k + 1. Son carré: 4k² + 4k + 1 divisé par 4 donne un reste de 1, donc (2k + 1) 1 mod 4. Son cube: (2k + 1) (2k + 1)² (2k + 1) x 1 = 2k + 1 mod 4 Etc. Exemples 3^2 = 9 = 2 x 4 + 1; 3^3 = 27 = 6 x 4 + 3; 3^5 = 243 = 60 x 4 + 3.

Voir Divisibilité des puissances

Devinette – Solution

Problème Trouver le nombre qui: divisé par 11 a un reste 4, divisé par 15 a un reste 10, et divisé par 19 a un reste 16. Solution Avec un tableur, la solution est simple ! Colonne 1, les nombres k successifs Colonne 2, les nombre n = 11k + 4 Colonne 3, valeurs de (n – 10) mod 15 Colonne 4, valeurs de (n – 16) mod 19 Colonne 5, test si mod = 0 en colonne 3 et 4. Si oui, c'est la bonne réponse. Le nombre n = 1 555 est la solution.

Extrait tableur Vérification 11 x 141 + 4 = 1 555 1 555 – 10 est divisible par 15 (= 103) 1 555 – 16 est divisible par 19 (= 81)

Retour / Autres énigmes / Restes chinois pour résoudre ce genre de problème

Suite	Algorithme du modulo 10 (de Luhn) Brève 367 – Calcul modulo en bref Calcul modulaire rapide (algorithme et programmation) Congruence – Théorie Cubes et somme de cubes modulo 9 Initiation au calcul Log modulaire Modulo 9, 10, 11 Modulo des carrés et des cubes Modulo des cubes Tour de magie avec les modulos
Voir	Application à la factorisation Clé de divisibilité, une application de la théorie du modulo La division Nombres congruents Petit théorème de Fermat Résidus quadratiques
Aussi	Calcul mental – Index Clé de divisibilité Divisibilité par 11 Fractions et horloge Géométrie – Index Nombres Cycliques Nombres Rationnels Preuve – Glossaire Preuve par 9 Preuve par 9 – Débutant Théorie des nombres – Index
Site	XModulorama de Richard Lefèbvre Une superbe application du calcul modulo. Animation de fils tendus.
DicoNombre	Nombre 105

Cette page

Introduction à l'arithmétique modulaire http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Modulo.htm

Renvois de liens

MODULO 10

MODULO 9

MODULO 11

INTÉRÊT DU MODULO Démonstration de divisibilité

PREUVES ET MODULO – Cas du modulo 8

MODULO & FERMAT

DESSINS MODULO

JEUX - Les œufs

JEUX - La somme