NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/12/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TABLES de NOMBRES
Débutants Général	Nombres à MOTIFS			Glossaire Général
INDEX Tables	Repunit	Repdigit	Pannumérique
	Multiples	Parasites	Magie 10001
	Chiffres distincts	Ondulant	Zigzag
	Premiers résistants	P–Repdigit	Retournés
	Sommaire de cette page >>> Table

Sommes algébriques PANNUMÉRIQUES

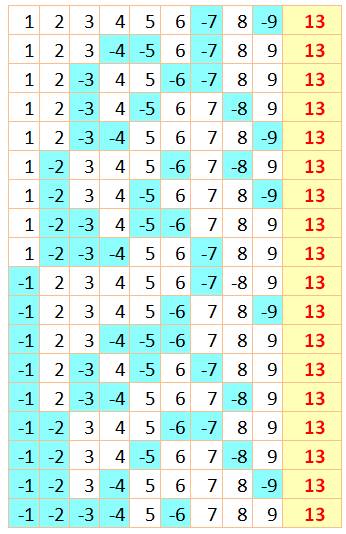
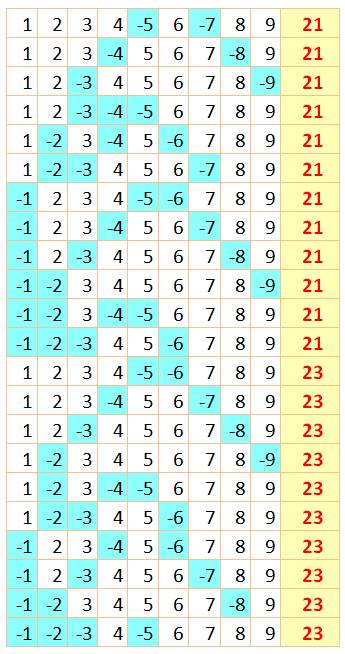
Sommes positives, en plus et moins, des neuf chiffres.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

Sachant que la somme est toujours impaire, dont en particulier, il est impossible d'obtenir zéro.

Les sommes négatives sont obtenues en inversant tous les signes.

Quantité de sommes selon le résultat:

Pour un grand total de 256.

Seule somme pannumérique de trois fractions avec un chiffre au numérateur et deux au dénominateur.

Sommes 3 3 3

Quelles sont les additions a + 2a = 3a pannumériques, chaque terme comportant trois chiffres?
Notez que l'on ne s'intéresse pas à la somme qui vaut 6a.

Il n'existe aucune telle addition avec plus de six chiffres différents.

Il y en a 34 avec six chiffres différents, dont les cinq du tableau qui présentent une succession des six chiffres. Le cas de 273 est pannumérique avec sa somme.

Pas mieux avec a + ka + ha. On retrouve, par exemple, 152 + 304 + 608 avec les chiffres de 0 à 5 pour k = 2 et h = 4.

Avec des termes à quatre chiffres:
1728 + 3456 + 5184 comporte les huit chiffres de 1 à 8.

Avec des termes à cinq chiffres:
13485 + 26970 + 40455 avec tous les chiffres de 0 à 9. C'est le plus petit parmi 31 cas.
32907 + 65814 + 98721 est le plus grand cas.

Table des sommes positives de 1 à 45

Voir	Pannumérique – Développements Repunit Nombres à motifs
Cette page	http://villemin.gerard.free.fr/TABLES/aaaMotif/SomPanNu.htm