|
||||||||||||
![]()
|
Famille |
Nombre / Diviseurs / Multiplicatif / Composé /
Plusieurs |
|
|
Approche |
|
15
est un multiple de 3 Car
15 = 5 fois 3. |
|
Définitions |
MULTIPLE D'UN ENTIER n Tout
nombre entier qui est divisible sans reste par l'entier considéré n. Multiple commun à plusieurs nombres Nombre
entier multiple de chacun des nombres considérés.
Le
plus petit multiple commun des nombres considérés >>> |
|
|
Exemples |
Les
multiples de 3 sont: 6, 9, 12, 15, 18, 21, 24, 27, 30 … Les multiples
de 37 sont: 74, 111, 148, 185, 222 … 63
est un multiple commun à 3 et à 7 car 63 = 21 fois 3 et 63 = 9 fois 7. 21
est le plus petit commun multiple de 3 et 7. |
|
|
Anglais |
Multiple
number |
|
|
En
physique, les fréquences multiples d'une fréquence
fondamentale sont des fréquences harmoniques. Un harmonique
est un son particulier ayant des fréquences multiples
de celles du son fondamental. La somme du fondamental et des harmoniques
forme le timbre. |
Voir
Sons / Physique
/ DicoMot

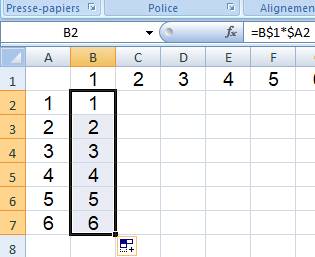
Notez qu'une ligne est identique à la colonne du même nombre
|
|
|
|
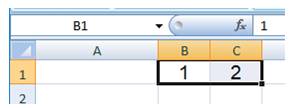
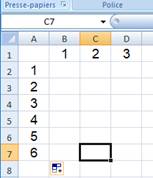
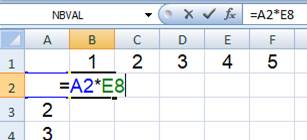
La création d'une table de multiplication sur tableur est un
excellent exercice pour l'apprentissage d'un tel outil. Par exemple:
désignation des cellules en relatif avec l'aide de symbole $.
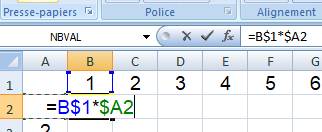
N'oubliez pas le DOLLAR sert à figer les
cellules utilisées dans les formules.
C'est fini. Vous obtenez le tableau montré
ci-dessous (extrait).
|
|
|
|
||
|
L'empreinte
en l'occurrence est la racine
numérique des multiples d'un nombre. Les
empreintes forment un cycle de 1, 3 ou 9 chiffres pour tous les multiples des
nombres. |
Pour le nombre 7 Ses multiples: 7, 14, 21, 28 … Les racines numériques: 7, 5, 3, 1 … En poursuivant, les racines forment un cycle continu avec (7, 5, 3, 1,
8, 6, 4, 2, 9). |
|
|
Table des racines numériques des nombres et de
leurs multiples
|
||
|
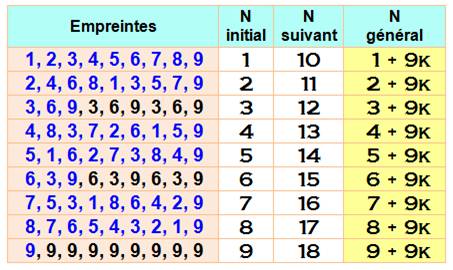
Empreintes des nombres et leur double cycle Les mêmes empreintes se retrouvent cycliquement pour
tous les multiples en m + 9k. Exemple: m = 13; ses multiples: 13, 26, 39 … ; son empreinte: (4, 8, 3 …).
C'est la même que le nombre 13 – 9 = 4. Table de multiplication Bouclons la boucle des multiples avec la table de
multiplication des nombres de 1 à 9. Table un particulière: on note la racine
numérique du produit (en l'occurrence, c'est aussi, le produit modulo 9). Les 0 sont remplacés par 9. Cette table est l'empreinte de toutes les empreintes! |
|
Anglais: the sum of digits for multiples of numbers
![]()
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/Multiple.htm |
![]()