|
|||||||||||||||||||||||||||||
![]()
|
Carrés PLUS QUE PARFAITS Carrés fortement magiques Carrés ENCHANTÉS Carrés magiques dont tous
les carrés 2x2 produisent la même somme.
Alors les pandiagonales, les carrés 3x3, les triangles
3x3 et les concaténations de nombres sont magiques. On se demande ce
qui leur manque pout être parfaits. Il en existe
48 d'ordre 4. |
Anglais: Most-perfect
magic squares / strongly magic squares
Carré plus
que parfait d'ordre 4 et toutes ses propriétés
|
|
||
|
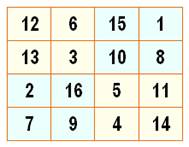
Ce carré
d'ordre 4 est magique: les sommes sur
lignes, colonnes et diagonales sont égales à 34 et les nombres dans la grille
vont de 1 à 15. Il est
aussi enchanté ou plus
que parfait: les sommes des quatre nombres dans les sous-carrés 2x2
sont égales à la constante magique 34.
|
|
|
Voir
Classement de tous les carrés magiques
d'ordre 4
|
|
||
|
Un carré
magique plus que parfait d'ordre n est
d'abord un carré magique,
et, il a
deux propriétés supplémentaires:
Tous les
carrés PQP sont d'ordre n = 4k. |
Carré
magique et un exemple de permutation
La colonne de gauche du second correspond à la région bas-gauche du
premier. Etc. Ces deux carrés sont plus que parfaits. De nombreuses transformations
conservent le carré enchanté. |
|
Les six propriétés
fondamentales du carré plus que parfait
|
De cette définition découlent de
nombreuses autres propriétés que nous énonçons et détaillerons ensuite (m est
la constante magique):
Rappel: pour tout carré magique d'ordre
4, il possible associer les seize nombres par paires de sorte que le total
soit égal à 34, la moitié de la
constante magique. >>> |
|
|
||
|
Utilisons
le tapis magique: le carré magique est
répété (autre image: imaginez que le carré est enroulé sur une sphère) Prenons
le premier carré 2x2 en haut à gauche et a somme des nombres: Faisons
glisser ce carré vers la droite et vers le bas (avec un tableur, c'est
immédiat). Les sommes sont inscrites dans le tableau du bas. En rouge les
sommes uniques et en noir les cas redondants. Ainsi: il
existe 16 carrés 2x2 présentant la somme magique. Notez que cette façon de faire permet de capter automatiquement la somme des quatre sommets (12 + 1 + 7 +
14) comme un carré 2x2 (encadré en bleu). Le carré central est lui aussi
automatiquement balayé grâce à ce procédé. |
Dans un carré plus que parfait, le carré glissant 2x2 (comme celui en bleu)
balaye 16 carrés qui somment tous en m, la constante magique. |
|
|
Les seize carrés 2x2 explicités À gauche,
les seize sous carrés 2 x 2 et à droite sept autres configurations dont
certaines peuvent s'imaginer comme des sous-carrés 2 x 2 à condition
d'enrouler le carré .
Bilan pour ce carré plus que
parfait: quantité de sommes magiques: Lignes /
colonne / diagonales (10) + pandiagonales (2 x 3) + carrés 2x2 (16) => 32. Notez que
les cas : 12 + 6 + 2 + 16 = 36 ne marchent pas. Remarquez
pour les quatre configurations en bas à droite (sommets des sous-carrés 3
x3): la somme des diagonales vaut 17 = m/2. |
||
|
|
||
|
Pour
visualiser les pandiagonales (ou diagonales secondaires), les répliques du
carré son juxtaposées comme indiqué. Les
encadrements de couleur montrent une des pandiagonales (8, 2, 9, 15). Il en
existe quatre en descendant et quatre en montant (somme en rouge); les autres
sont identiques. Avec ce
carré particulier toutes les pandiagonales produisent une somme identique. Le
carré est panmagique. |
Dans un carré 4x4, il y a deux diagonales
principales (12, 3, 5, 14 et 1, 10, 16, 7) et six pandiagonales: |
|
|
|
||
|
Observation 12 + 5 =
2 + 15 = m/2 6 + 11 = 16 + 1 = m/2 13 + 4 = 10 +
7 = m/2 3 + 14 =
8 + 9 = m/2 Démonstration: les quatre coins |
|
|
|
Dans les
carrés 2x2, trois coins et un central pour se concentrer dans le triangle
supérieur gauche |
A1 = m – (A2 + B1 + B2) A3 = m – (A4 + B3 + B4) C1 = m – (C2 + D1 + D2) C3 = m – (C2 + B2 + B3) |
|
|
La somme
des termes à soustraire sont montré par une croix. On y voit: une ligne, une
colonne et une diagonale soit une somme de 3m. |
|
|
|
La somme
des quatre coins |
A1 + A3 + C1 + C3 = 4 m – 3 m =
m = 34 |
|
|
Démonstration: deux à deux |
|
|
|
Évaluations
des quatre sommets en fonctions des équerres indiquées |
A1 = 34 – (A2 + B1 + B2) C3 = 34 – (B2 + B3 + C2) A3 = 34 – (A2 + B2 + B3) C1 = 34 – (B1 + B2 + C2) |
|
|
En observant
les termes |
A1 + C3 = A3 + C1 |
|
|
|
||
|
Dominos horizontaux 12 + 6 =
10 + 8 = 2 + 16 = 4 + 14 = 18 15 + 1 =
13 + 3 = 5 + 11 = 7 + 9 = 16 = 34 – 18 Dominos verticaux 12 + 13 =
16 + 9 = 15 + 10 = 11 + 14 = 25 2 + 7 = 6
+ 3 = 5 + 4 = 1 + 8 = 9 = 34 – 25 Démonstration Dans le
rectangle A1C2 en haut à gauche, par exemple: A1 + A2 + B1 + B2 = m C1 + C2 + B1 + B2 = m A1 + A2 = C1 + C2 |
Les dominos jaunes somment en 18 et les
bleus en 16, avec 16 + 18 = 34. Même propriété pour les dominos verticaux. |
|
|
|
||
|
La somme
des nombres dans les triangles
rectangles 3x3 est égale à 3/2 de la somme magique. Il a 4 x 16
configurations. Exemples (un pour chacune des quatre orientations): 12 +
6 + 15 + 13 + 3 + 2 = 51 7 +
9 + 4 + 2 + 16 + 13 = 51 14 +
4 + 9 + 11 + 5 +
8 = 51 Explication
|
Tous les triangles rectangles 3x3 somment
en 51 = 34 + 17 |
|
|
|
||
|
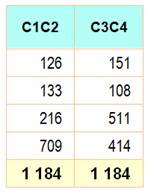
Les
nombres de deux colonnes sont juxtaposés pour donner de nouveaux nombres. Exemple
avec les colonnes 1 et 2 puis 3 et 4. La somme des nombres obtenue est la
même. Propriété
vraie pour toutes les combinaisons pour aboutir à deux sommes différentes
seulement. Suite en amusement décimal |
|
|
Un
autre carré plus que parfait d'ordre 4
|
Carré magique avec
|
|
![]()
Autres carrés plus que parfait
|
|
||
|
Ce carré
magique est exceptionnel puisque les 64 carrés 2 x 2 somment en 130. Les
couples en diagonale, séparés de quatre pas, somment en 65 = 8² + 1. Par
exemple: 1 + 64 ou encore12 + 53. Diagonales
et pandiagonales montantes et descendantes (2 x 64) somment également en
260. Varin=ante
du carré du haut, les deux carrés 4x4 en jaune sont conservés et les deux
autres remaniés. Notez que
les quatre nombres de chaque ligne sont conservés: ils ont été simplement
inversés (57, 7, 59, 5 devient ( 5, 59, 7, 57). |
|
|
|
Kathleen Ollerenshaw (1912-2014) et David S. Brée donnent une méthode de construction et d'énumération
de tous les carrés magiques plus que parfaits. dans leur livre: Most-perfect Pandiagonal Magic Squares: Their
Construction and Enumeration (1998). Ordre 4:
48 Ordre 8:
368 640 Ordre 12: 2,22953 1010 Ordre 16: 9,32243 1014 Ordre 36: 2,76754 1044 |
|
|
||
|
Soit n un
nombre |
|
|
|
Doublement
pair (divisible par 4) |
p1 = 2 et S1 >1 |
|
|
Sa
quantité de diviseurs |
|
|
|
Avec |
|
|
|
Et |
|
|
|
Quantité
de carrés magiques plus que parfaits |
|
|
![]()
Construction
– Principe
|
|
||
|
Carré n
|
Réversible: une colonne et son inversée: les
sommes deux à deux sont égales. 0 4 8
12 12 8 4
0 12 12 12 12 |
|
|
Kathleen Ollerenshaw et David S. Brée ont montré que tout carré réversible d'ordre 4k peut
être transformé, selon une procédure mise au point par eux, en un carré
magique plus que parfait; et que tous sont produit par cette procédure. La construction proposée fait appel à des combinaisons de matrices.
Cependant, pour l'ordre 4, il est possible de résumer la procédure comme
suit. |
||
|
Pour
construire un carré plus que parfait, inverser les deux colonnes de droite |
|
|
|
Inverser
les deux lignes du bas |
|
|
|
En
divisant le carré 4x4 en carrés 2x2, et pour chacun:
La figure
du haut montre ces mouvements pour chacun des carrés 2x2, avec la position
finale de nombres en rouge. Notez l'effet d'enroulement classique pour loger
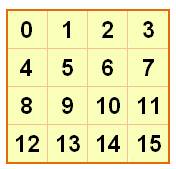
les nombres qui sortent du cadre. Le carré
4x4 du centre récapitule ces positions et donne un carré magique plus que
parfait mathématique (nombres de 0 à 15). Le carré
4x4 du bas est le carré plus que parfait classique (nombres de 1 à 16). |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/CarEnch.htm
|
![]()