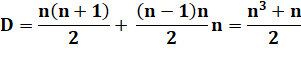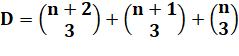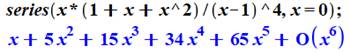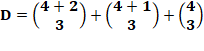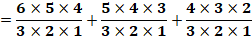Carré des nombres entiers

Édition du: 12/12/2023

INDEX Carrés magiques Magie Jeux de grilles Jeux et énigmes Calculs	GRILLES – Carrés magiques
	Permutations figurées	Latin	Gréco-latin
	Symétrie	Tapis (prog)	Math des tissus
	Tours indépendantes	Test QCM	Carré des entiers

Faites un double-clic pour un retour en haut de page

Carré des entiers

Les n² premiers entiers sont disposés dans grille n×n.

Les sommes sont chacune des diagonales principales sont égales.

Sommaire de cette page

>>> Approche

>>> Calcul de la somme sur diagonale

Débutants

Carrés magiques

Glossaire

Carrés magiques

Approche

haut

Méthode

Les n² nombres entiers sont disposés en lignes puis en colonnes dans une grille carrée de n cases par côtés.

Somme sur les deux diagonales

Elles sont égales.

Elles valent: ½ n (n²+ 1))

Somme magique

Ces nombres sont également la constante magique des carrés magiques ordinaires.

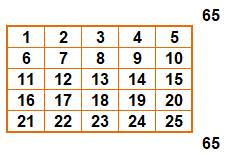
Illustration pour n de 2 à 5

Pour 34, la somme vaut: ½ 4 (4² + 1) = ½ 4×17 = 34

Voir Brève 56-1102

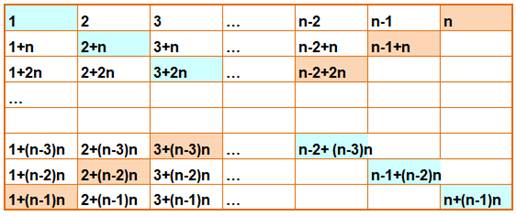
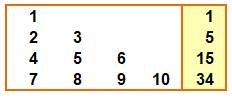
Calcul de la somme sur diagonale			haut
Grille générique Disposition des nombres sur une grille n×n. Observez les éléments sur chacune des diagonales (coloration). On y trouve d'abord la somme de tous les nombres de 1 à n. On doit y ajouter des produits avec le facteur n en commun et les nombres de 1 à (n-1) comme second facteur.	Illustration pour n de 2 à 4 Somme sur chacune des diagonales Dd = 1 + (2+n) + (3+2n) + … + (n+(n-1)n Dm = 1+(n-1)n + 2+(n-2)n + … + n-1+n + n
Somme sur chacune des diagonales On connait la somme des nombres de 1 à n: s = ½ n (n+1) Ce qui conduit à l'expression: Autre formule Fonction génératrice Voir Fonctions génératrices		Sommes pour n à partir de 0 0, 1, 5, 15, 34, 65, 111, 175, 260, 369, 505, 671, 870, 1105, 1379, 1695, 2056, 2465, 2925, 3439, 4010, 4641, 5335, 6095, 6924, 7825, 8801, 9855, 10990, 12209, 13515, 14911, 16400, 17985, 19669, 21455, 23346, 25345, 27455, 29679, 32020, 34481, 37065, 39775, … OEIS A006003 Exemple: Somme de coefficients binomiaux
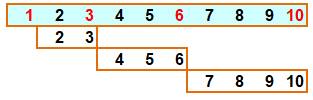
Somme de n nombres Ces nombres sont aussi la somme de n nombres consécutifs, chacune des sommes prise les unes à la suite des autres. C'est aussi la somme des nombres compris entre T_n-1 + 1 et T_n, avec T_n le nombre triangulaire de rang n. (En rouge sur l'illustration, les nombres triangulaires)		Somme de nombres consécutifs Relation avec les nombres triangulaires

Haut de page (ou double-clic)

Retour	Carrés magiques et symétries Carrés des tissus
Suite	Carrés magiques – Index Symétries dans le carré magique
Voir	Jeux – Index Jeux de nombres – Index Jeux numériques – Index Pavages Rectangles magiques
Sites	*OEIS A006003 – a(n) = n(n^2 + 1)/2 OEIS A209297 - Triangle read by rows: T(n,k) = kn + k - n, 1 <= k <= n*
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/CarrEnti.htm