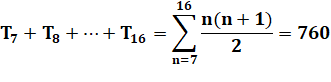|
||||||||||||||||||||||||||||
![]()
Nombre triangle et billard: T5 = 15 boules

|
|
|||||
|
Famille |
|||||
|
Définitions |
NOMBRE TRIANGULAIRE ou NOMBRE TRIANGLE
|
||||
|
Formule |
|
||||
|
Un qui se fait remarquer |
1 + 2 + 3 + 4 = 10 |
||||
|
Fonction génératrice |
|
||||
|
Propriétés |
En effet, parmi les deux facteurs n et n+1, l'un d'eux
est pair (disons: 2k) et c'est lui qui est divisé par 2 pour donner:
Dans l'un ou l'autre cas, Tn est un nombre
composé à deux facteurs.
|
||||
|
Racine triangulaire |
Voir Racine triangulaire |
||||
|
Angl |
|
||||
|
Direct
Via définition d'une fonction
|
Voir Programmation – Index
|
Calcul de la formule Sachant
que la suite des nombres triangulaires est: 1, 3,
6, 10, 15, 21 Quelle
est la formule définissant chacun ? Les
écarts sont en progression arithmétique. Il s'agit d'une fonction quadratique;
cad. du deuxième degré en ax² + bx + c. Écrivons
trois relations avec les nombres connus et résolvons ce système de trois
équations à trois inconnues. |
Résolution du système d'équations
Bilan
|
Voir Brève
de Maths 490
|
|
||||
|
n P 1 1 2 3 3 6 4 10 5 15 6 21 7 28 8 36 9 45 10
55 11
66 12
78 13
91 14 105 15 120 16 136 17 153 18 171 19 190 20 210 21 231 22 253 23 276 24 300 25 325 |
n P
27 378 28 406 29 435 30 465 31 496 32 528 33 561 34 595 35 630 36 666 37 703 38 741 39 780 40 820 41 861 42 903 43 946 44 990 45 1 035 46 1 081 47 1 128 48 1 176 49 1 225 |
n P 50 1 275 51 1 326 52 1 378 53 1 431 54 1 485 55 1 540 56 1 596 57 1 653 58 1 711 59 1 770 60 1 830 61 1 891 62 1 953 63 2 016 64 2 080 65 2 145 66 2 211 67 2 278 68 2 346 69 2 415 70 2 485 71 2 556 72 2 628 73 2 701 74 2 775 |
n P 75 2 850 76 2 926 77 3 003 78 3 081 79 3 160 80 3 240 81 3 321 82 3 403 83 3 486 84 3 570 85 3 655 86 3 741 87 3 828 88 3 916 89 4 005 90 4 095 91 4 186 92 4 278 93 4 371 94 4 465 95 4 560 96 4 656 97 4 753 98 4 851 99 4 950 100 5 050 … |
|
|
Suite des nombres triangulaires
pour n jusqu'à 250 0, 1, 3, 6, 10, 15, 21, 28, 36, 45,
55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325,
351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820,
861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431,
1485, 1540, 1596, 1653, 1711, 1770, 1830, 1891, 1953, 2016, 2080, 2145, 2211,
2278, 2346, 2415, 2485, 2556, 2628, 2701, 2775, 2850, 2926, 3003, 3081, 3160,
3240, 3321, 3403, 3486, 3570, 3655, 3741, 3828, 3916, 4005, 4095, 4186, 4278,
4371, 4465, 4560, 4656, 4753, 4851, 4950, 5050, 5151, 5253, 5356, 5460, 5565,
5671, 5778, 5886, 5995, 6105, 6216, 6328, 6441, 6555, 6670, 6786, 6903, 7021,
7140, 7260, 7381, 7503, 7626, 7750, 7875, 8001, 8128, 8256, 8385, 8515, 8646,
8778, 8911, 9045, 9180, 9316, 9453, 9591, 9730, 9870, 10011, 10153, 10296,
10440, 10585, 10731, 10878, 11026, 11175, 11325, 11476, 11628, 11781, 11935,
12090, 12246, 12403, 12561, 12720, 12880, 13041, 13203, 13366, 13530, 13695,
13861, 14028, 14196, 14365, 14535, 14706, 14878, 15051, 15225, 15400, 15576,
15753, 15931, 16110, 16290, 16471, 16653, 16836, 17020, 17205, 17391, 17578,
17766, 17955, 18145, 18336, 18528, 18721, 18915, 19110, 19306, 19503, 19701,
19900, 20100, 20301, 20503, 20706, 20910, 21115, 21321, 21528, 21736, 21945,
22155, 22366, 22578, 22791, 23005, 23220, 23436, 23653, 23871, 24090, 24310,
24531, 24753, 24976, 25200, 25425, 25651, 25878, 26106, 26335, 26565, 26796,
27028, 27261, 27495, 27730, 27966, 28203, 28441, 28680, 28920, 29161, 29403,
29646, 29890, 30135, 30381, 30628, 30876, 31125, 31375. |
||||
|
|
||
|
Nombre
triangulaires palindromes T10 =
55 T132
= 8778 T173
= 15051 T363
= 66066 … |
Nombres
triangulaires carrés T1 = 1 =
1² … |
|
|
|
||
|
L Extrait du triangle de Pascal
Ces nombres sont le développement des puiss Ils donnent l Les
nombres triangulaires sont en fait la quantité de combinaisons de 2
objets parmi n C'est
notamment la quantité de segments qui joignent n points non alignés |
||
|
Tn = C2n+1 |
Exemples T3 = C24 = 6 T10 = C211
= 55 |
|
|
|
||
|
Exemple de lecture: ligne 7 et
colonne 16: 760 La somme des nombres triangulaires de 7 à 16 est égale à 760. |
|
|
|
La diagonale liste les nombres triangulaires. La première ligne forme les nombre tétraédriques.
Le nombre 10
est les deux à la fois. Nombres somme de triangulaires (les 320 nombres ordonnés jusqu'à
2000) 0, 1, 3, 4, 6, 9, 10,
15, 16, 19, 20, 21, 25, 28, 31, 34, 35, 36,
45, 46, 49, 52, 55, 56, 64, 66, 74, 78, 80, 81, 83, 84, 85, 91, 100, 105, 109, 110, 116, 119, 120, 121, 130, 136,
144, 145, 153, 155, 161, 164, 165, 166, 169,
171, 185, 190, 196, 199, 200, 202, 210, 216,
219, 220, 225, 230, 231, 235, 244, 251, 253, 256, 266, 274, 276, 280, 282, 285, 286, 289, 290, 300, 308, 316,
324, 325, 329, 335, 340, 344, 351, 354, 360, 361,
363, 364, 371, 378, 394, 395, 399, 400, 406, 409, 420, 435, 440, 441, 445, 451, 452, 454, 455, 460, 465, 476, 484, 496, 504, 514, 515, 525, 528, 529, 530, 540, 550, 556, 559, 560, 561, 571, 576, 580, 595, 596, 605, 624, 625, 630, 631, 645, 650, 651, 660,
666, 670, 676, 679, 680, 683, 685, 694, 696,
703, 724, 729, 732, 741, 749, 760, 770, 776,
780, 781, 784, 796, 802, 804, 806, 812, 815, 816, 820, 829, 841, 849, 854,
860, 861, 875, 884, 885, 900, 901, 903, 913, 920, 934, 946, 949, 955, 959,
961, 965, 966, 968, 969, 970, 975, 976, 980, 990, 1020, 1024, 1035, 1044,
1054, 1055, 1056, 1060, 1081, 1084, 1085, 1089, 1091, 1105, 1110, 1120, 1128,
1130, 1135, 1136, 1139, 1140, 1154, 1156, 1160, 1165, 1176, 1208, 1210, 1211, 1219, 1225,
1246, 1252, 1254, 1270, 1274, 1275, 1295, 1296, 1306, 1310, 1316, 1320, 1326, 1329, 1330, 1331, 1344, 1354, 1369,
1375, 1385, 1396, 1407, 1420, 1444, 1456, 1460,
1464, 1484, 1485, 1489, 1505, 1520, 1521, 1530, 1536, 1539, 1540, 1551,
1569, 1570, 1585, 1595, 1600, 1606, 1620, 1630, 1631, 1651, 1660, 1681, 1684, 1687, 1715, 1736,
1738, 1740, 1751, 1760, 1761, 1764, 1767, 1770, 1771, 1784, 1785, 1786, 1802,
1804, 1845, 1849, 1859, 1883, 1891, 1895, 1904, 1920, 1924, 1936, 1940, 1946, 1956, 1968, 1989, 1999. En rouge les sommes doubles
|
||
Accès à chacun
de ces nombres par le DicoNombre /
Somme de 3 triangulaires
/ Égalité de sommes de 3
Triangulaires
|
Une paire de nombres triangulaires dont la somme
comme la différence sont aussi des nombres triangulaires: 15, 21,
36, 6 105, 171,
276, 66 378, 703,
1081, 325 780, 990,
1770, 210 1485,
4186, 5671, 2701 2145,
3741, 5886, 1596 5460,
6786, 12246, 1326 7875,
8778, 16653, 903 21945,
38781, 60726, 16836 29403,
30628, 60031, 1225 37950,
219453, 257403, 181503 61425, 203203,
264628, 141778 61425,
416328, 477753, 354903 70125,
77028, 147153, 6903 105570,
188191, 293761, 82621 |
Suite et programmation Quadruplets de
triangulaires
|
|
||
|
On sait
que tout nombre est somme
de trois triangulaires, au plus. Mais,
chaque nombre possède sans doute plus de partitions en nombres triangulaires.
La quantité va croissant ! |
Quantité de partitions en nombres triangulaires Ex: Pt(10) = 7, Pt(11) = 7 , Pt(50) = 417 1, 1, 1, 2, 2, 2, 4, 4, 4, 6, 7, 7, 10, 11, 11, 15, 17, 17, 22, 24, 25, 32, 35, 36,
44, 48,
50, 60, 66, 68, 81, 89, 92, 107, 117, 121, 141, 153, 159, 181, 197, 205, 233,
252, 262, 295, 320, 332, 372, 401, 417, 465, 501,
520, 575, 619, 645, 710, 763, … |
|
|
Les partitions triangulaires pour n de 1 à
20 [n, quantité de partition,
partitions] La quantité de '1' est indicée pou alléger l'écriture. Pour retrouver n,
il suffit d'ajouter l'indice aux nombres qui suivent. Rappel : premiers nombres triangulaires: 1, 3, 6, 10, 15, 21
|
||
![]()
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()