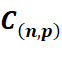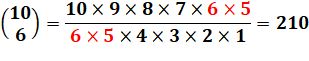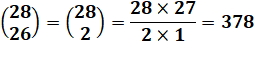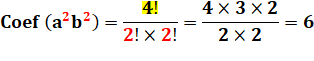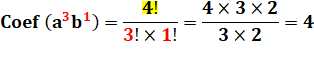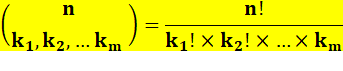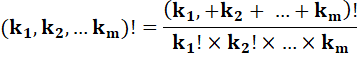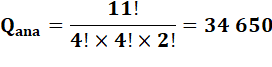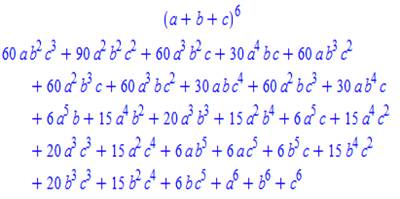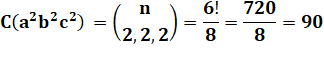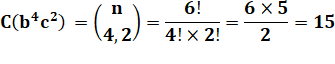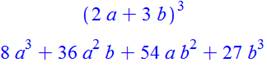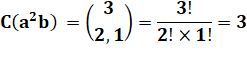NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 22/06/2023

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

COMPTER

 

Débutants

Compter

Coefficients du BINÔME

 

Glossaire

Compter

 

 

INDEX

COMBINATOIRE

 

Triangle de Pascal

Partie 1

Partie 2

 

Sommaire de cette page

>>> Notations

>>> Triangle de Pascal

>>> Pratique

>>> Règle pratique

>>> Astuce

>>> Coefficients multinomiaux

 

 

 

 

Aussi: coefficients binomiaux,

Binôme de Newton (énoncé en 1665)

 

Un tableau de nombres

utile à diverses applications.

 

*    On connaît le développement d'une somme algébrique à une puissance donnée.

 

*    On utilise ses propriétés dans la démonstration du petit théorème de Fermat.

 

*    Le triangle de Pascal est particulièrement utile pour dénombrer les combinaisons.

 

Célèbre formule qui sert à créer

le triangle de Pascal

 

 

 

 

Exemple avec disposition

dans le triangle de Pascal

 

4

+

6

 

=

10

 

Un nombre est égal à

-        celui du dessus plus

-         celui de dessus-gauche.

 

Voir Triangle de Pascal / Pascal

 

 

 

NOTATIONS

 

Cette notion de coefficient du binôme sert
à calculer aussi bien:

*    les coefficients du binôme (bien sûr),

*    les nombres figurant dans le triangle de Pascal,

*    la quantité de combinaisons de p objets parmi n,

*    la quantité de combinaisons de n objets pris p à p,

*    la quantité de p-combinaisons,

*    la quantité de partitions d'un ensemble.

 

 

 

Notations françaises

Notations américaines

Commentaires

Différentes

 

Les Français utilisent aussi la lettre

k au lieu de p

 

Les Américains utilisent plutôt la lettre

r au lieu de p

Normalisée

 

 

 

 

 

TRIANGLE de PASCAL ou

Triangle arithmétique (comme l'appelait Pascal)

 

Tableau

p =

0

1

2

3

4

5

6

7

8

9

10

11

12

n = 0

1

 

 

 

 

 

 

 

 

 

 

 

 

1

1

1

 

 

 

 

 

 

 

 

 

 

 

2

1

2

1

 

 

 

 

 

 

 

 

 

 

3

1

3

3

1

 

 

 

 

 

 

 

 

 

4

1

4

6

4

1

 

 

 

 

 

 

 

 

5

1

5

10

10

5

1

 

 

 

 

 

 

 

6

1

6

15

20

15

6

1

 

 

 

 

 

 

7

1

7

21

35

35

21

7

1

 

 

 

 

 

8

1

8

28

56

70

56

28

8

1

 

 

 

 

9

1

9

36

84

126

126

84

36

9

1

 

 

 

10

1

10

45

120

210

252

210

120

45

10

1

 

 

11

1

11

55

165

330

462

462

330

165

55

11

1

 

12

1

12

66

220

495

792

924

792

495

220

66

12

1

 

Exemple 10 = 4 + 6

Suite en  Triangle de Pascal

 

 

Application aux combinaisons

*    Un sac contient 5 billes

*    J'en tire 2

Combien de possibilités?

Cpn = C25 = 10

*    Un examen comporte 5 questions

*    L'élève doit répondre à 3 d'entre-elles

Combien de possibilités?

Cpn = C35 = 10

*    Un comité comporte 10 personnes

*    Un sous-comité de 4 personnes doit être formé

Combien de possibilités?

Cpn = C410 = 210

 

 

 

PRATIQUE

 

Écrivons la formule de calcul sous cette forme:

 

C0n =

n!

soit

n

…

n-p+1

…

 

 

 

x 2

x 1

divisé par

(n-p)!

"

 

 

 

n-p

….

 

 

x 2

x 1

et encore par

p!

"

 

 

 

 

 

p

…

x 2

x 1

 

 

Simplifions par (n-p)!

On retire la partie verte du milieu et la partie correspondante du jaune

Le tableau devient:

 

C0n =

n!

soit

n

…

n-p+1

 

 

 

 

 

divisé par

(n-p)!

"

 

 

 

 

 

 

 

 

et encore par

p!

"

 

 

 

dddddd    

p

…

x 2

x 1

 

 

Il reste la fraction suivante:

Cpn =

 

n (n-1) …    p facteurs

 

 

p (p-1) …    p facteurs

 

 

 

Exemples

C38 =

 

8 x 7 x 6

= 4 x 7 x 2 = 56

 

3 x 2 x 1

 

C410 =

 

10 x 9 x 8 x 7

= 5 x 3 x 2 x 7 = 210

 

4 x 3 x 2 x 1

 

En image

 

On pose 10 en haut et 4 en bas. Quatre termes décroissants en haut et quatre termes décroissants en bas.

On procède à toutes les simplifications possibles avant de calculer. Ici, tout le dénominateur disparait: 2 et 4 avec 8 et 3 avec 9. Il reste 10 x 3 x 7 = 210.

 

 

 

Astuce

 

Deux formules équivalentes dues à une propriété des coefficients du binôme qui sont symétriques.

 

Selon le cas, il est préférable de prendre l'une ou l'autre; la plus courte.

 

 

Exemple =>

 

 

 

La somme des deux nombres en bas vaut le nombre en haut.

 

 

Voir Combinaisons – Introduction

 

 

 

Généralisation – Coefficients multinomiaux

 

Les coefficients multinomiaux (ou coefficients du multinôme) sont à la puissance n ce que sont les coefficients binomiaux à la puissance 2.

Ils permettent notamment de connaitre la valeur d'un polynôme élevé à une puissance quelconque sans effectuer le développement.

 

 

(a + b)2 = a2 + 2ab + b2

(a + b)3 = a3 + 3a2b + 3ab2 + b3

(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4

 

Voir Identités remarquables

 

 

Exemple

Quel est le coefficient de a²b² dans le développement de (a + b) à la puissance 4 ?

Et pour a3 b ?

 



 

Formulation

 

Notez que la somme des k est égale à n.

Autre notation

Application

Quantité de combinaisons avec répétitions de m éléments ayant une multiplicité ki .

Énigme classique

Combien d'anagramme du mot Mississippi?

n = 11; avec : 1 m, 4 i, 4 s et 2 p.

 

Voir Suite de cet exemple avec contraintes  / Autres exemples

 

Notez que la plus grande anagramme dans le dictionnaire est "pipis"

Exemple

 

 

 

 

 

Avec des coefficients dans le polynôme

 

 

À multiplier par la puissance des coefficients:

         2² x 3 = 12

C = 3 x 12 = 36

 

Même pas peur …

dont un des coefficients est:

 

Son calcul

à multiplier par: 22 x 35 x 13 = 972

C = 2 530 x 972 = 2 449 440

 

Anglais: Multinomial coefficient

Voir Multiensembles

 

 

 

 

 

Suite

*  Relations et formules

*  Loi binomiale

Retour

*    Combinatoire – Rubriques

*    D'un coup d'œil

Voir

*    Cartes

*    Compter les nombres

*    Dés

*    Dés – Somme s pour n dès à x faces

*    Dominos

*    Échecs

*    Factorielle et ses cousines

*    Grenouilles

*    Identités (a+b)n

*    Jeux

*    Polynômes

*    Probabilités

*    Triangle de Pascal

Cette page

http://villemin.gerard.free.fr/Denombre/CombBino.htm