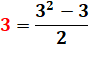Nombres avec chiffres 7, 8 ou 9

Édition du: 23/12/2023

INDEX Chiffres Types de nombres	CHIFFRES – Fréquence
	Nombre normal	Probabilité	Loi de Benford
	Quantité de couples	Auto-descriptifs	Combinaisons
	Chiffres en nombres	Nombres en nombres	Chiffres 7 8 9

Faites un double-clic pour un retour en haut de page

Nombres avec chiffres 7, 8 ou 9

Compter les nombres formés avec les seuls chiffres 7, 8 ou 9.

Sommaire de cette page

>>> Quantité de N₇₈₉

>>> Fractions avec les entiers

>>> Pesées

>>> Autres configurations

Débutants

Nombres

Glossaire

Nombres

Quantité de N₇₈₉		haut
	Quantité de nombres jusqu'à 9 ne comportant que les chiffres 7, 8 ou 9. Ce sont: 7, 8, 9.
	Quantité de nombres jusqu'à 99 ne comportant que les chiffres 7, 8 ou 9. Ce sont: 7, 8, 9, 77, 78, 79, 87, 88, 89, 97, 98, 99.
	Quantité de nombres jusqu'à 999 ne comportant que les chiffres 7, 8 ou 9. Ce sont: 7, 8, 9, 77, 78, 79, 87, 88, 89, 97, 98, 99, 777, 778, 779, 787, 788, 789, 797, 798, 799, 877, 878, 879, 887, 888, 889, 897, 898, 899, 977, 978, 979, 987, 988, 989, 997, 998, 999.
	Quantité de nombres jusqu'à 9 999 ne comportant que les chiffres 7, 8 ou 9. Ce sont: 7, 8, 9, 77, 78, 79, 87, 88, 89, 97, 98, 99, 777, 778, 779, 787, 788, 789, 797, 798, 799, 877, 878, 879, 887, 888, 889, 897, 898, 899, 977, 978, 979, 987, 988, 989, 997, 998, 999, 7777, 7778, 7779, 7787, 7788, 7789, 7797, 7798, 7799, 7877, 7878, 7879, 7887, 7888, 7889, 7897, 7898, 7899, 7977, 7978, 7979, 7987, 7988, 7989, 7997, 7998, 7999, 8777, 8778, 8779, 8787, 8788, 8789, 8797, 8798, 8799, 8877, 8878, 8879, 8887, 8888, 8889, 8897, 8898, 8899, 8977, 8978, 8979, 8987, 8988, 8989, 8997, 8998, 8999, 9777, 9778, 9779, 9787, 9788, 9789, 9797, 9798, 9799, 9877, 9878, 9879, 9887, 9888, 9889, 9897, 9898, 9899, 9977, 9978, 9979, 9987, 9988, 9989, 9997, 9998, 9999.
	Quantité de nombres jusqu'à 10^n-1 – 1 ne comportant que les chiffres 7, 8 ou 9. Cette relation est une conjecture même si abondamment vérifiée.
Liste	0, 3, 12, 39, 120, 363, 1092, 3279, 9840, 29523, 88572, 265719, 797160, 2391483, 7174452, 21523359, 64570080, 193710243, 581130732, 1743392199, 5230176600, 15690529803, 47071589412, 141214768239, …

Voir DicoNombre 12 / 39 / 120

Fractions avec les entiers

haut

Comment arranger les nombres successifs en fractions entières.

Les dénominateurs sont les nombres vus-ci-dessus en:
(3ⁿ – 3) / 2.

Et la valeur de la fraction est en:
2 × 3ⁿ – 1.

Pesées		haut
C'est aussi le plus grand nombre de poids identiques parmi lesquels un intrus peut être identifié et on peut décider si cet intrus est plus lourd ou plus léger, en utilisant n pesées avec une balance à plateaux. Dans le cas où il faut identifier l'intrus, alors la relation devient: (3ⁿ – 1) / 2 et on a: 4, 13, 40 …	Ces relations en puissances de 3 sont impliquées dans certains problèmes mathématiques concernant des pesées. L'un de ces problèmes est le suivant : De combien de poids avez-vous besoin pour pouvoir peser des objets pesant jusqu'à 40 grammes sur une balance à deux plateaux ? La réponse est 4 poids, de 1, 3, 9 et 27 grammes. Un autre problème: De combien de pesées avez-vous besoin pour déterminer laquelle des 13 pièces a un poids différent, si vous savez avec certitude qu'une seule est différente ? La réponse est trois pesées.
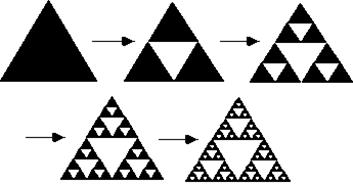
Cette dernière suite est aussi celle comptant les triangles dans un triangle de Sierpinski. 1, 5, 17, 53, 161 … Ne pas oublier de compter les triangles de toutes tailles. En deuxième position, il y a bien 4 petits triangles et un grand, soit 5 triangles.

Autres configurations		haut
Nombres N₀₁₂	0 à 99 : 8 0 à 999 : 26 0 à 9999: 80
Nombres N₁₂₃	0 à 99 : 12 0 à 999 : 39 0 à 9999: 120
Nombres N₂₃₄	0 à 99 : 12 0 à 999 : 39 0 à 9999: 120
Nombres N₁₂₃₄	0 à 99 : 20 0 à 999 : 84 0 à 9999: 340

Haut de page (ou double-clic)

Retour	Quantité et fréquence des chiffres
Suite	Nombres en nombres
Voir	Chiffres – Index Dénombrement – Index Loi de Benford Loi équirépartie	Nombres auto-descriptifs Paradoxes Probabilités
Sites	OEIS A029858 – a(n) = (3^n – 3)/2. *OEIS 048473 – a(0)=1, a(n) = 3a(n-1) + 2; a(n) = 23^n - 1*
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/Chiff789.htm