|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mono: une bille
est plus lourde (ou plus légère) Ambi: une
bille est plus lourde ou plus légère
sans que nous le sachions a priori |
![]()
|
Énigmes de pesée – Introduction |
|
|
Les problèmes
de balance ou de pesée sont des énigmes logiques qui demandent à
trouver une pièce, une bille, une balle ou une boule qui serait plus lourde
ou plus légère que toutes les autres et ceci à l'aide d'une balance à
plateaux (Roberval) en un nombre donné de pesées. Aucun poids n'est admis. |
Le fameux problème des douze billes, réputé insoluble. |
Voir Brève 53-1047
|
19
balles de 10, 20, 30, … 190 grammes,
de trois types. Les
9 en ivoire pèsent 900 grammes de plus que les 9 en plastique. Il en reste
une en bois dont on demande quel est son poids. |
|
|
||
|
Énigmes
de pesées avec poids connus |
Quelle est la
combinaison de poids qui permet toutes les pesées jusqu'à k kilogrammes. Elles s'apparentent aux énigmes de
transvasements. |
|
|
Énigmes
de pesées avec poids
inconnus |
Poids avec étiquettes de poids mélangées |
|
|
Dans tous les
types d'énigmes de pesée sans poids On utilise une balance à plateau pour détecter un intrus. Tous les objets
sont visuellement identiques. L'un d'eux n'a
pas le même poids. Voir Débutants |
|
|
Nature de
l'intrus et |
L'intrus est présent, et:
⇨
trouver l'intrus
⇨
trouver l'intrus et dire sa nature, ou ⇨
simplement trouver l'intrus. Il est présent ou non: ⇨
dire s'il est présent et si oui, dire lequel et préciser sa nature. |
|
Deux
intrus de même nature |
Les deux intrus sont présents, ils tous deux plus lourds ou plus
légers. Avec trois pesées, on détecte deux intrus dans un maximum de cinq
pièces. La méthode par dichotomie est la seule applicable. Pas de solution
pas combinaisons. |
|
Extension
multi-balance |
Un intrus plus lourd ou moins lourd; Deux balances à plateau sont
utilisées en parallèle (extension à k balances). Chaque pesée dure une
minute. Quel est le plus grand nombre n de billes desquelles trouver la bille
fautive. Puzzle de Konstantin Knop – 2012 |
Noms de ces énigmes dans la littérature et sur
Internet
|
Énigmes des douze
billes Énigmes des neuf
boules Énigmes des
quatre billes Pesée des douze
pièces Problème de la
fausse pièce de monnaie Problème des 80
billes Problème des
douze pièces Problème des
quatre boules Les sacs et une
seule pesée Les fausses
pièces Les sacs de
pièces d'or |
A fake among eight coins Balance puzzle Coin puzzle, coin problem Coin-weighing puzzle Single counterfeit coin problem (SCCP) Six misnamed coins, two weighings The famous 12 balls problem The nine balls problem Weighing puzzle Weighing 10 bags puzzle |
|
|
||
|
Cas du problème des
neuf pièces Le
problème des neuf pièces apparait dans la
littérature en 1945 dans American Mathematical Monthly par E. D. Schell. Les
neuf pièces pèsent la même chose, sauf une qui est plus lourde et qu'il faut
isoler en deux pesées. |
Il
se trouve deux pesées est le minimum de pesées pour trouver une pièce fausse
parmi neuf et neuf est d'ailleurs le maximum. Une pièce de plus et il faudra
trois pesées. |
|
|
Cas du problème des
douze billes Ce problème m'a été soumis par mon
voisin de siège d'avion lors d'un voyage de retour d'Australie en 1981.
J'avais alors trouvé la solution indiquée sur ces pages Cette énigme m'avait été
proposée avec des boules
de billard. Elle passait, pour la communauté de
celui qui me la posait, pour impossible à résoudre. |
Beaucoup
plus tard, j'ai découvert le
texte de Jacques Lacan relatant
que ce problème avait été inventé par François Le Lionnais, célèbre
mathématicien et rapporté par Raymond
Queneau. Sous
sa forme originelle, le problème est relatif à la pesée de pièces de monnaie dont une est une fausse pièce. Martin
Gardner dans le Scientific American résous
ce problème en utilisant la base
ternaire de numération. La
solution a été utilisée par des magiciens
pour déterminer la fausse pièce en trois pesées sous les yeux ébahis des
spectateurs … De
nombreux mathématiciens amateurs de jeux mathématiques ont donné leurs
propres solutions: Dyson et Lyness,
Conway, Bundy, Steinhaus … |
|
|
|
|||
|
Dénombrement Pour pouvoir effectuer une pesée, la
quantité de billes doit être supérieure à 1, évidemment. Le tableau montre le maximum de
billes impliquées dans une énigme de n billes en k pesées. On retrouve (jaune) les deux énigmes
classiques:
|
Tableau pour les deux
types d'énigmes
Évidemment,
qui peut le plus peut le moins. Par exemple,
le problème des 80 billes exige
quatre pesées. |
||
|
Formalisation
|
|||
|
Énigme |
On
sait que la bille fautive est plus lourde ou plus légère et on demande de
trouver laquelle sans préciser la nature. Alors,
la formule devient:
Soit,
une bille de plus que pour le cas où il faut préciser la nature. Ainsi avec
trois pesées, on peut discriminer la fautive parmi treize. En
fait on peut résoudre le sous-défi de 12 billes et y trouver l bille fautive
et sa nature comme d'habitude. Si on le l'a pas trouvée (trois équilibres de
suite), c'est que c'est la treizième qui est fautive et on n'a pas de
possibilité de pesée pour déterminer sa nature. |
||
|
|
||
|
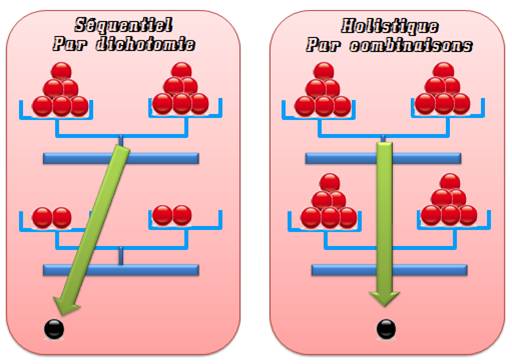
Deux
grandes catégories de solutions à ce genre d'énigmes de pesées. La méthode
holistique étant très utile pour résoudre les plus
complexes: |
||
|
On procède par pesées successives comportant de
moins en moins de billes (méthode séquentielle).
La bille fautive est contenue dans des groupes de
billes de plus en plus petits (dichotomie) |
On procède aux pesées avec la même quantité de
billes à chaque fois, pas les mêmes évidemment (méthode non-séquentielle ou holistique). La combinaison
des issues de pesées conduit à la bille fautive. |
|
|
|
||
|
|
||
|
Balance puzzle Weighing puzzle Balance scale Two-pan balance Fake coin Counterfeit coin Heavier Lighter The right pan rises The scale remains balanced To figure out To devise |
A balance puzzle or
weighing puzzle is a logic puzzle about balancing items, often coins, to
determine which holds a different value, by using balance scales a limited
number of times. These differ from puzzles that assign weights to items, in
that only the relative mass of these items is relevant. Given 9 coins, one of
them fake and lighter, find the fake coin in two weighings on a balance
scale. So to minimize the number
of weighings, we need to divide all the coins into three piles. There are twelve coins.
One of them is fake. All real coins weigh the same. The fake coin is either
lighter or heavier than the real coins. Find the fake coin and figure
out whether it is heavier or lighter in three weighings on a balance scale. Using only a two-pan
weighing balance, we must devise a weighing scheme to identify the
counterfeit coin and determine whether it is heavier or lighter. |
|
Voir Anglais – Le bagage minimum
|
Énigme 19 balles de 10, 20, …190 grammes, de trois types. Les
9 en ivoire pèsent 900 grammes de plus que les 9 en plastique. Il en reste
une en bois dont on demande quel est son poids. Réponse: x = le poids des
plus lourdes, y = celui des plus légères et z = celui de la balle unique. Poids
total: x + y + z = 10 (1 + 2 + … + 19) = 10 x 19 x 20 / 2 =
1900 g Poids min de 9 balles: 10 (1 + 2 + … + 9) = 10 x 9 x 10
/ 2 = 450 g Poids max de 9 balles: 10 (11 + 12 + … + 19) = 10 x 90
+ 10 (1 + 2 + … + 9) = 900 x 450 = 1 350 g. Différence entre poids max et poids min: 1 350 – 450 = 900 g Différence entre les poids des balles en ivoire et en
plastique: x = y + 900 Pas d'autre choix que: prendre les neufs balles en
ivoire parmi les neuf plus lourdes et les neufs en plastique parmi les neuf
plus légères. Celle en bois et donc la balle intermédiaire: elle pèse
100 g. Vérification Ivoire : 1 350 g; Bois : 100 g; Plastic: 450 g =>
total = 1 900 g |
Énigme
de ce type publiée par le journal Libération du 13 avril 2018
en partenariat avec Images des Mathématiques, Insmi CNRS,
Ana Rechtman
![]()
|
Retour |
|
|
|
|
|
Voir |
|
|
|
|
Sites français |
|
|
Sites anglais |
|
|
Sites avancés |
|
![]()