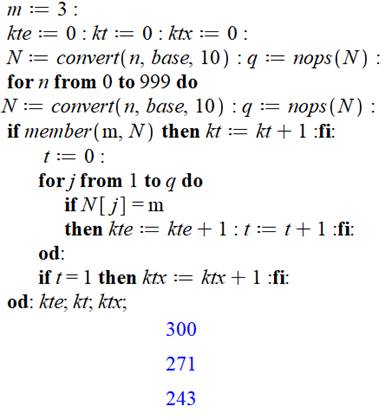|
|||||||||||||||||||||||||||||
|
Quantité et fréquence des CHIFFRES Sur cette page:
|
Nombres auto-descriptif
(self-descriptive numbers)
|
Nombres dont les
chiffres indiquent la quantité de chiffres qu'il contient. Par exemple: 2020 nous
indique qu'il contient deux fois le "0" et deux fois le
"2". |
Voir Nombre
6 210 001 000
Pour commencer
|
pour
écrire tous les nombres jusqu'à N |
|
||
|
1 |
Q = N |
Q1 = 1 Q9 = 9 |
|
|
10 |
Q = 9 + 2(N – 9) = 2N – 9 |
Q10 = 11 Q99 = 189 |
|
|
100 |
Q = 189 + 3(N – 99) = 3N – 108 |
Q100 = 192 Q999 = 2 889 |
|
|
1000 |
Q = 2889 + 4(N – 999) =
4N – 1107 |
Q1000 = 2 893 Q9999 = 38 889 |
|
Exemples
|
Combien
de chiffres pour paginer un livre de 300 pages: Q300
= 3 x 300 – 108 = 792 chiffres. Combien
de chiffres pour numéroter les 52 maisons de la rue: Q52
= 2 x 52 – 9 = 95 plaques de chiffres. |
Voir Quantité de lettres pour écrire les
nombres
|
|
||
|
Exemple avec le
chiffre 3. Dans une
centaine, le chiffre 3 est présent:
La quantité de 3 pour la tranche de 0 à 99
est: Q100 = 20 En tenant
compte du nombre privilégié 33, il y a
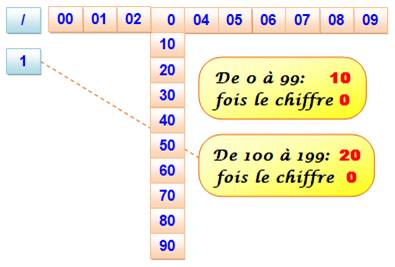
Cas du chiffre 0. De 0 à
99, le chiffre 0 est présent 10 fois Dans une
centaine, autre que la première, le
chiffre 0 est présent 20 fois. |
Présence du chiffre 3
dans une centaine
Présence du chiffre 0
dans les centaines
|
|
|
Présence du 3 de 0 à
999 |
Dans
chaque centaine: 10 fois 20 = 200 Chiffre
des centaines: 100 Total :
300 fois le chiffre 3 pour les nombres de 0 à 999. Présent
dans 271 nombres et dans 243 de façon unique. |
|
Présence du 0 de 0 à
999 |
Dans la première
centaine: 10 fois le 0 Dans les
neuf autres: 9 fois 20 = 180 Chiffre
des centaines: 0 Total :
190 fois le chiffre 0 pour les nombres de 0 à 999. Présent
dans 181 nombres et dans 172 de façon unique. |
|
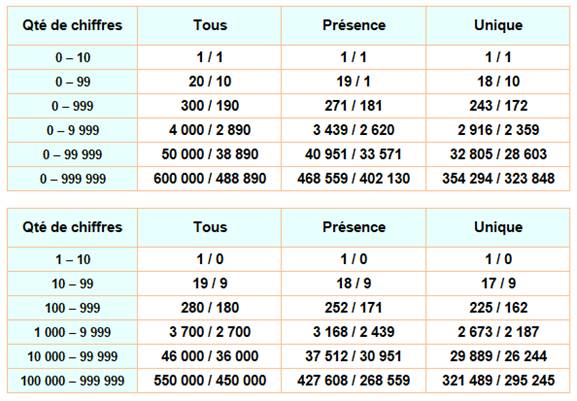
Bilan Quantité de chiffres de 0 à N puis
par plages Exemple de lecture De 0 à 999, il y a 300 nombres avec
un chiffre donné, sauf pour le 0 avec 190 chiffres seulement. Ce chiffre est présent dans 271
nombres; 181 nombres pour le 0. Ce chiffre est présent une seule
fois dans 243 nombres; 172 nombres pour le 0. |
|
|
Formulation PRÉSENCE |
La quantité de
nombres ayant le chiffre m (une ou plusieurs fois) est donné par la formule
réurente suivante: |
|
TOUS dans
une plage en puissance de10 |
On écrit 99…9k
un nombe comportant k fois le chiffre 9. Pour un plage de 0 à 99…9k ,
la quantité de chiffres, autre que 0, est égale à:
Pour la
quantité de 0:
|
|
|
||
|
Programme de comptage du chiffre m
dans une plage donnée de nombres
|
Commentaires Le chiffre à compter est en m. kte compte la totalité des chiffres m; kt, la quantité de nombres avec m présent, et ktx, la quantité de nombres avec un seul m. La plage de recherche est définit en lançant la
boucle en n Les chiffres de n sont placés en N (effet de convert). Si le chiffe appartient à cette liste de chiffre
(member), le compteur kt est incrémenté. Avec l'indicateur t, on recherche combine de fois
m est présent dans N. Le compteur kte est alimenté en conséquence. Si ce compteur vaut 1, le compter ktx est
incrémenté. En bleu les résultats pour la plage 0 – 999. Pour la plage 0 à 1234 et le chiffre 3, on aurait
respectivement: 349, 317 et 286. Pour la plage 0 à 9876 et le chiffre 9, on aurait
respectivement: 3 744, 3 316 et 2 905. |
|
|
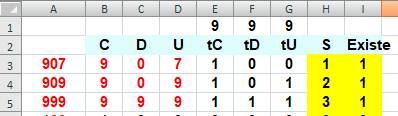
Avec un tableur
Avec 999, le tableur détecte bien trois 9 (colonne S) et signale en
colonne I, qu'il existe au moins un 9 dans ce nombre. En pied de tableau, on peut faire la somme de ces valeurs. Instructions à placer B3: =CNUM(STXT($A3;1;1)) C3:
=CNUM(STXT($A3;2;1)) D3:
=CNUM(STXT($A3;3;1)) E3:
=SI(B3=$E$1;1;0) F3:
=SI(C3=$F$1;1;0) G3: =SI(D3=$G$1;1;0) H3: =SOMME(E3:G3) I3:
=SI(H3>0;1;0) |
Commentaires Un bon moyen de s'entrainer à la pratique du tableur. Les nombres sont en colonne B, la valeur du
chiffre à tester est en F9 et recopiée en G9 et H9. En B3, C3 et D3: extraction des chiffres de n qui
est en A3. En F3, G3 et H3: test si le chiffre m est
présent. Si oui, l'indicateur est mis à 1 sinon 0. En H3: somme des indicateurs, témoin de la
quantité de présence de m dans n En I3: mis à 1 si la somme n'est pas nulle. |
|
Voir Programmation – Index
|
|
||
|
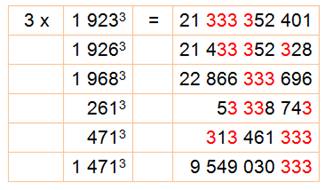
Origine de cette
recherche Clifford Pickover donne ces exemples avec le bloc
333. Il examine les nombres de la forme 3n3 contenant au moins le
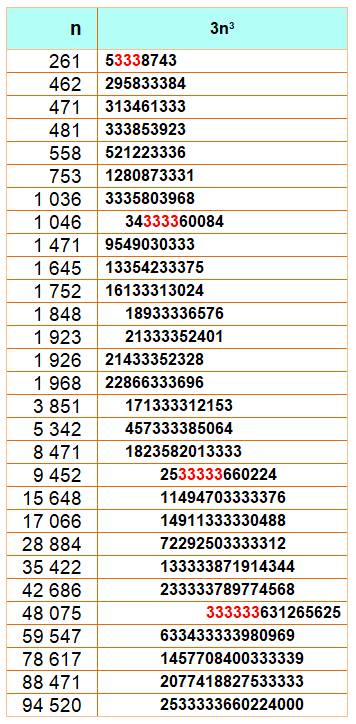
bloc 333. Une recherche systématique montre que la quantité
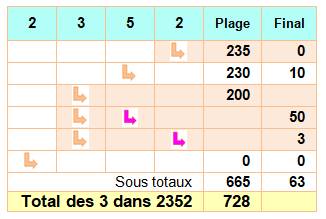
de ces nombres est plus grande comme le montre ce tableau du bas. Tableau Le
décalage des nombres dans le tableau témoigne d'une quantité de plus en plus
grande des blocs de 3 consécutifs: de 3 à 6. Programme de recherche
des blocs de chiffres
Commentaires La
procédure convertit le nombre n en un liste de chiffres (convert); quantité
de chiffres en q. La boucle
en i compare chaque chiffre à la consigne m et compte la quantité (kt). Si un
autre chiffre que m survient, kt est mis à zéro après avoir mémoriser la
quantité comptée. Cette
quantité 'locale" est comparée à la quantité mémorisée (ktm) pour ne
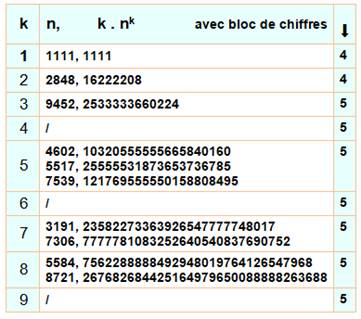
conserver que la plus grande quantité. Autres cas Est-ce une particularité du
nombre 3 ? Non, pas vraiment. Le tableau suivant montre le
résultat d'une recherche pour le chiffre k pour les nombres en k . nk. Ils sont assez nombreux pour
quatre chiffres identiques de suite. On n'a listé, sauf pour 1 et 2, que les
nombres avec bloc de 5. |
Tableau suite à
recherche systématique
|
|
Voir Programmation – Index
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
