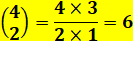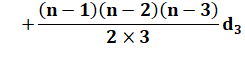|
Édition du: 28/01/2022 |
|
INDEX |
SUITES NUMÉRIQUES Méthode des différences |
||
Faites un double-clic pour un retour en haut de page
![]()
|
SUITES – Méthode des différences Coefficients binomiaux Étant donné une
suite de nombres, et sans développer le tableau des valeurs et des
différences:
La méthode des
différences successives conduira à la mise en évidence des coefficients
binomiaux (le triangle
de Pascal). Un moyen pratique pour résoudre quantité de problèmes sur les
suites de nombres, notamment le calcul simple de formules comme, par exemple
celle de la somme
des cubes. |
||
|
|
Sommaire de cette page >>> Trouver le premier terme d'une k-différence >>> Exemple et formulation >>> Exemple de calcul avec cinquième différence >>> Calcul du nième élément >>> Formule de la somme de n termes |
Débutants Glossaire |
|
k-différence |
Une suite numérique est une énumération de
nombres (y) dont le rang est donné par la suite des nombres entiers (x). La première différence d1 est celle
calculée entre les éléments successifs de la suite. La k-différence dk est celle calculée
entre les différences k-1 successives. Notre but est de trouver le premier nombre de
chaque k-différence.
|
||||||||||||||||||||||||||||||||||||
|
Calcul des k-différences |
Nommons (a, b, c, d, …) la suite y des nombres. Calculons les différences sur la ligne
précédente.
Celles qui retiennent notre attention sont celles
de tête, en jaune. Comment les calculer sans développer le tableau ?
Notre seule connaissance est la valeur du premier
terme (a) et les différences de tête d1, d2, d3
…. |
||||||||||||||||||||||||||||||||||||
|
Logique de la construction |
On reprend le tableau précédent et on essaie de
trouver la logique de formation des différences successives. Après avoir calculé la première différence d1,
on reporte des valeurs sur la ligne du bas en décalant et en opposant la
valeur. En explicitant la soustraction, on montre comment est calculée la
prochaine différence (rouge). On observe que, au signe près, les coefficients
qui se créent sont les nombres du triangle
de Pascal, autrement-dit, les coefficients
binomiaux. |
|
Tableau de construction des
k-différences
|
|
|
Suite |
Suite à travailler: 1, 8, 27, 64, 125 (ce sont les valeurs de x+1 au cube). On se propose de calculer les nombres de tête des
k-différences. On les connait en développant le tableau des
différences, mais voyons le résultat via l'utilisation des nombres du
triangle de Pascal. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Pour info |
Tableau des résultats attendus
|
Triangle de Pascal
Exemple de calcul d'un coefficient
Mêmes nombres dans la
fraction puis les suivants, autant que le nombre du bas. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
d2 |
Les trois coefficients de la ligne 2 du triangle de pascal (1, 2, 1)
servent à pondérer les trois premières valeurs de la suite (1, 8, 27). La
somme est alternée.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
d3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
d4 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Formulation Avec les coefficients binomiaux et leur forme développée |
La formule s'applique pour les rangs pairs et l'opposée
pour les rangs impairs Deux formes possibles pour la formule:
Valeur de tête des différences kièmes. Pour la
différence dixième, n = 10, par exemple.
Il s'agit de la somme alternée, dont le sens
dépend de la parité du rang, des premières valeurs de la suite pondérées par
les coefficients binomiaux. |
|
|
Formule explicitée pour quatrième
différence constante |
|
|
|
Suite: 30, 31, 32,
33, 34, 35, … On veut calculer le nombre de tête de la
différence cinquième. Le rang est impair, il faut prendre la valeur
opposée. Les coefficients du binôme sont: 1, 5, 10, 10, 5, 1. d5T = – ( 1 – 3×5 + 9×10 – 27×10 + 81×5 – 243 ) Remarque importante Cette suite de puissances ne produit jamais de
différence nulle. C'est une suite exponentielle et non pas polynomiale. |
Calcul des différences successives
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Construction du tableau ci-dessous 1ère colonne: reprenons l'expression
des nombres de tête. 2e colonne: calculons les valeurs de
a, b, c, d, … 3e colonne: remplaçons b, c, d … autant que possible par les nombres di
de tête de chaque différence. |
Bilan La troisième colonne (à droite) montre à nouveau
un procédé de création des coefficients du binôme. |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
Exemple
Vérification La suite: (1, 4, 8, 13, 19, 24, 30, 37, 45, 54,
64, …) |
Question Donner le dixième nombre de la série Nécessite Les trois premiers nombres de la ligne 10 du
triangle de Pascal: 1, 9, 36. Trois valeurs, pour atteindre une différence
constante. Calcul pour n = 10
|
|||||||||||||||||||||||||
|
Formule |
Valeur du nième élément d'une suite connaissant les valeurs de tête di
des k-différences successives (attention: signe + partout):
|
|||||||||||||||||||||||||||||||
|
Exemple
|
Question Donner le douzième nombre de la série Nécessite Quatre termes pour atteindre une différence
constante. Calcul pour n = 12
Nombre qui est bien le cube de 12. |
|||||||||||||||||||||||||||||||
|
Voir Partage du
cercle y0 = 1 d = {1, 1, 1, 1} Tous calculs faits: |
|
|||||||||||||||||||||||||||||||
Voir Brève
849
|
Calcul des premières sommes (tableau) Les nombres de la suite (b, c, d, …) sont
remplacés par leur valeur en fonction des différences (comme calculé
précédemment). S1, S2 … sont les nombres de la suite et Observation On retrouve les coefficients du binôme. |
|
||
|
Formule Note: a = y0 |
Somme des n premiers termes d'une suite en
fonction des nombres de tête des différences successives:
La somme est égale à:
|
||
|
Somme des impairs
Voir
Somme
des impairs |
|
||||||||||||||||||||||||
|
Somme des carrés
Voir
Somme
des carrés |
|
||||||||||||||||||||||||
|
Somme de cette suite
|
|
||||||||||||||||||||||||
|
Somme des cubes
Voir Somme des
cubes |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Suite/aSuite/SuiDif03.htm
|