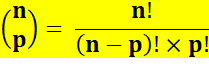NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/07/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ITÉRATIONS
Débutants Général	TRIANGLE de PASCAL				Glossaire Général
INDEX Itérations	Approche	Formules	Propriétés	Historique
	Triangle	Valeurs	Fractal	Puissance 11
		Binôme	Divisibilité
	Sommaire de cette page >>> TRIANGLE DE PASCAL dans sa présentation classique du triangle isocèle

TRIANGLE DE PASCAL

Présentation classique du triangle isocèle.

TRIANGLE DE PASCAL

Voir suite en Triangle Pascal jusqu'au rang 30 et plus

Voir Factorielle et triangle de Pascal / Nombres de Stirling

Lecture
Chaque nombre du triangle de Pascal est un coefficient du binôme ou coefficient du énième terme du développement de l'élévation à la puissance p du binôme: (a + b)^n. Pour lire un coefficient se souvenir que la première valeur sur une ligne occupe le rang 0. C'est aussi la quantité de combinaisons de n objets pris p par p. La formule étant: Voir Calcul pratique	C7^3 = 7! / 3! (7-3)! = 5040 / (6 x 24) = 35 C7^4 = 7! / 4! (7-4)! = 5040 / (24 x 6) = 35 C20^10 = 184 756 Pour la ligne 20, la colonne centrale atteint 184 756

Suite	Triangle de Pascal – Fractales Combinaisons – Toutes les formules Pascal – Biographie
Voir	Combinaisons Formule du binôme Petit théorème de Fermat Calcul des sinus et cosinus des angles en Pi / n
Aussi	Géométrie – Index Récurrence Théorie des nombres
Site	Pour d'autres représentations du triangle Pascal voir le site: Pascal / Images
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/TrgPascT.htm