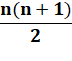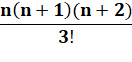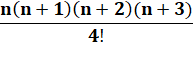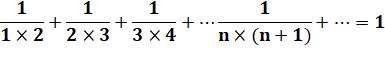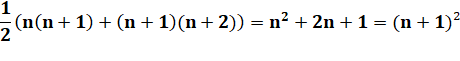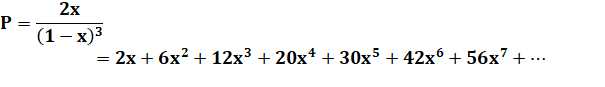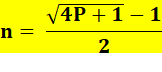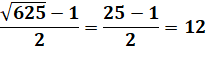|
||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PRONIQUES ou PROMIQUES, OBLONGS,
PRESQUE-CARRÉS, RECTANGULAIRES, HÉTÉROMÈQUES ou encore hétéroméciques Quantité associée à
un rectangle dont longueur et largueur sont égales
à 1 près.
Un nombre pronique,
produit de deux nombres successifs, est aussi la somme des nombres pairs ou en
encore la somme de deux nombres
triangulaires identiques. Np
= n (n + 1) = 2 + 4 + 6 + … 2n Pronique
viendrait du grec promekes, rectangulaire, oblong. |
Anglais: pronic number or promic numbers, or oblong number or
heteromecic number
|
|
||
|
Définition |
Nombres proniques ou nombres
oblongs:
|
|
|
Exemple |
272 = 16 x 17
qui est aussi palindrome. |
|
|
Liste des premiers |
|
|
|
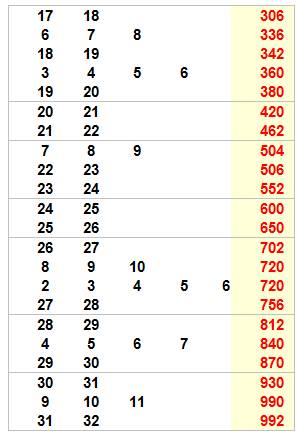
À la suite |
0, 2, 6,
12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380,
420, 462, 506, 552, 600, 650, 702, 756, 812, 870, 930, 992, 1056, 1122, 1190,
1260, 1332, 1406, 1482, 1560, 1640, 1722, 1806, 1892, 1980, 2070, 2162, 2256,
2352, 2450, 2550, … |
|
|
Carrés |
Terminés
par 25, ces nombres sont les carrés des nombres terminés par 5. |
|
|
Nombres |
Nombres proniques |
quasi
proniques |
Nombres |
Nombres pentatopes |
|
|
|
|
|
|
|
Nombres Hexa-2 |
||||
|
|
Curiosité
|
P(73737)
= 73737 x 73738 = 5 437 218 906 Ce
nombre pronique d'indice ondulant
est pannumérique; il contient tout les
chiffres de 0 à 9. |
|
|
||
|
Général |
n² + n = n(n+1) =
2 x (1 + 2 + … + n) = 2 + 4 + … + 2n |
|
|
Somme |
Les sommes successives étant: 1/2, 2/3, 3/4, 4/5 …
n/n+1. Démonstration >>>
|
||
|
Différence |
On – On-1 = 2n |
n
(n + 1) – (n – 1) n =
n² + n – n² + n =
2n |
272 – 240
= 32 = 16 x 17
– 15 x 16 = 2 x 16 =
32 |
|
On+1 – On = 2n + 2 |
(n
+ 1) (n + 2) – n (n + 1) =
n (n + 1) + 2 (n + 1) – n (n + 1) =
2 (n + 1) |
||
Illustration: passage d'un oblong au
suivant
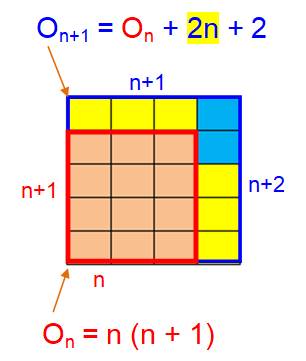
|
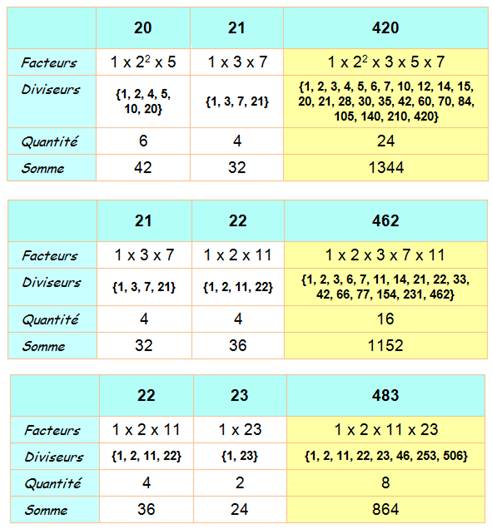
Divisibilité |
Exemples
|
|
Types |
Ex: 6 7 8 9 10
11 12 Le carré 9 est à la même distance des
nombres 6 et 12.
|
|
Exercice d'algèbre** |
Pouvez que N = (n ² + n – 1)(n² + 3n + 1) + 1 est
pronique N = n4 + 4n3 + 3n2 –
2n = n (n + 2) (n2 + 2n – 1)
= (n2
+ 2n) (n2 + 2n – 1) = K (K – 1) |
|
Fonction génératrice** |
|
|
|
|||||||||||||||||||
|
Sn = 1x2 + 2x3
+ 3x4 + 4x5 + … + n(n+1) =
1/3 n (n + 1) (n + 2) Un
tiers du produit des trois nombres consécutifs à partir de n.
Sn = 1x2 + 2x3
+ 3x4 + 4x5 + … + (n² + n)
Sn = { 1/2 n(n+1) } + {
1/6 n (n+1)(2n+1) } Après
mise en facteurs: Sn = n (n+1)
{ 1/2 + 1/6 (2n+1)
} Sn = n
(n+1) ( 3/6 +
2n/6 + 1/6 ) Sn
= n (n+1) ( n/3 + 2/3 ) Sn
= n (n+1) (n+2) / 3
|
|||||||||||||||||||
|
Démonstration
("astucieuse") utilisant les polynômes S
= 1.2 + 2.3 + 3.4 + … + n(n + 1) = A + Bn + Cn2 + Dn3 +
En4 + … Avec A, B, C, D … variables indépendantes de n. Avec n devenant n + 1 1.2
+ 2.3 + 3.4 + … + n(n + 1) + (n + 1)(n + 2) =
A + B(n + 1) + C(n + 1)2 + D(n + 1)3 + E(n + 1)4
+ … En faisant la soustraction des deux (tous calculs
faits): (n
+ 1)(n + 2) = B + C(2n + 1) + D(3n²
+3n + 1) + E(4n3 + 6n² + 4n + 1) + … Le premier membre est du deuxième degré; le second
l'est également, donc tous les coefficients à partir de E sont nuls. (n
+ 1)(n + 2) = B + C(2n + 1) + D(3n²
+3n + 1) n²
+ 3n + 2 = 3Dn² + (2C + 3D)n+ B + C + D Soit le système d'équations 3D
= 1 D = 1/3 2C
+ 3D = 3 C = 1 B
+ C + D = 2 B = 2/3 Notre somme devient: S = A + 2/3n + 1/3n² + n3 Or S
(1) = 1.2 = 2 = A + 2/3 + 1/3 + 1 = A + 2 => A = 0 Formule
finale: S = n3 + 1/3 n² + 2/3 n |
|||||||||||||||||||
|
Démonstration
identique pour la somme suivante: Sn = 1.2.3
+ 2.3.4 + 3.4.5 + … + n(n + 1)(n + 2) =
A + Bn + Cn2 + Dn3 + En4 + Fn5… Sn+1 = 1.2.3 + 2.3.4 +
3.4.5 + … + n(n + 1)(n + 2) + (n + 1)(n + 2)(n + 3) =
A + B(n+1) + C(n+2)2 + D(n+3)3 + E(n+4)4 +
F(n+1)n5 … Sn+1 – Sn = (n
+ 1)(n + 2)(n + 3) = B + C(2n + 1) + D(3n² + 3n + 1) + E(4n3 +
6n² + 4n + 1) + … = n3 +
6n2 + 11n + 6 = 4E n3 + (6E + 3D) n2 + (4E +
3D + 2C) n + (E + D + C + B) Sn = A + 3/2 n + 11/4 n2 + 3/2 n3 +
1/4 n4 Sn (1) = 6 = A + 3/2
+ 11/4 + 3/2 + 1/4 = 6 => A = 0 Formule Sn = 3/2 n + 11/4 n2
+ 3/2 n3 + 1/4 n4
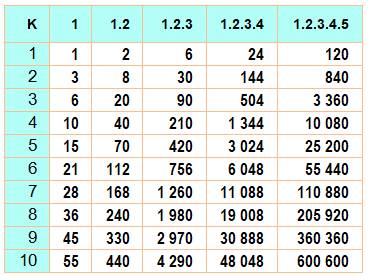
= (n3 + 6n2 + 11n + 6) n/4 Sn = 1/4 n (n + 1) (n + 2) (n + 3) Verification Sn (3) = 1.2.3 + 2.3.4 +
3.4.5 = 6 + 24 + 60 = 90 = 3/2 x 3 + 11/4 x 9 + 3/2 x 27 + 1/4 x 81 = 90 Valeurs pour n de 1 à
10 [1,
6], [2, 30], [3, 90], [4, 210], [5, 420], [6, 756], [7, 1260], [8, 1980], [9,
2970], [10, 4290] |
|||||||||||||||||||
|
|||||||||||||||||||
Voir Recherche
de formule de sommes / Autres démonstrations
semblables
|
|
|
|
Démonstration directe
Cette quantité tend vers 1
lorsque n tend vers l'infini. Démonstration par induction
|
|
Voir Demonstration par recurrence
|
|
||
|
Définition |
|
|
|
Exemples |
16 x 17 = 272 77 x 78 = 6 006 |
|
|
Propriétés |
|
|
|
Le premier |
Les nombres 2 et 6 sont proniques palindromes triviaux.
Le premier véritable est 272. |
|
|
Table |
Pour
dossier complet: voir site de Patrick
De Geest |
|
|
Le plus grand connu |
Warut
Roonguthai août 1997 |
|
|
Curiosité |
Suite qui se construit en mettant 45 54 ou 54 45 au
centre d'un nombre de départ. Malheureusement cette suite est finie.
|
|
|
|
||
|
Définition |
|
|
|
Exemple |
60 = 3 x 4 x 5 24 = 2 x 3 x 4 |
|
|
Propriétés des 3-proniques |
|
|
|
Multi-proniques Tables
(<1000) Ces nombres ne sont jamais des puissances parfaites (prouvé par Erdös
et Selfridge). Ces nombres sont le rapport entre deux factorielles: x! / y! Ce sont
des factorielles
tronquées. |
|
|
|
Suivants |
|
|
|
|
||
|
Racine pronique
Ex: Avec P = 156 retrouvez n = 12. 12 est la racine pronique
de 156. |
Exemple
|
|
|
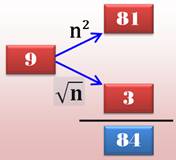
Autre vision
N = n4 + n = n (n3 + 1) |
3 est la racine pronique de 84. |
|
![]()
|
Suite |
|
|
Nombres géométriques |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Pronique.htm
|
![]()