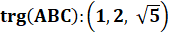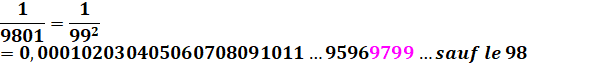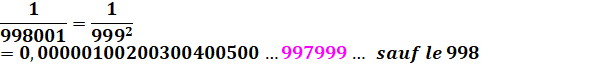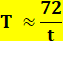|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 43 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
840. Triangles équilatéraux singuliers |
|
||||
|
Toutes les mesures indiquées sont
des nombres entiers Cas d'un point interne Ce triangle
équilatéral de côté 112 est le plus petit triangle équilatéral tel qu'il existe
un point D interne dont les distances aux trois sommets sont des nombres
entiers. |
|
||||
|
Cas d'un point quelconque Ce triangle
équilatéral de côté 7 est le plus petit triangle équilatéral tel qu'il existe
un point dont les distances aux trois sommets sont des nombres entiers. |
|
||||
|
Cas d'un point sur une côté Ce triangle
équilatéral de côté 8 est le plus petit triangle équilatéral tel qu'il existe
un point sur un côté dont les distances aux trois sommets sont des nombres
entiers. |
|
||||
|
Brèves associées |
>>>
Triangle
entier |
>>>
Brèves Géométrie – Index |
|||
|
Pour en savoir plus |
>>>
Triangle équialtéral et distances entières |
>>>
Nombre 7 >>>
Nombre 112 |
|||
841. Quatre nombres consécutifs |
|
|||||||||||||||||||||||||||||||||
|
Observation Le produit des quatre premiers nombres vaut: Autrement-dit: un carré mois un. Idée ? Propriété Le produit de quatre nombres consécutifs est égal
à un carré diminué de 1. n (n + 1) (n + 2) (n + 3) = (n² + 3n + 1)² – 1 |
Produits pour n de 1 à 10
|
|||||||||||||||||||||||||||||||||
|
Brèves associées |
>>>
Amusement avec les carrés |
>>>
Brèves Identités – Index |
||||||||||||||||||||||||||||||||
|
Pour en savoir plus |
>>>
Défis avec produit et carré |
>>>
Nombres consécutifs – Index >>>
Nombre 120 |
||||||||||||||||||||||||||||||||
842. Semi-uniforme divisible par 3 et 7 |
|
|||
|
Ce nombre proposé par E. Dudeney est
semi-uniforme: composé de deux chiffres seulement. C'est le plus petit avec 3 et 7 qui est divisible
par chacun de ses chiffres et dont la somme des chiffres l'est aussi. |
Un tel nombre contient trois "7" et
sept "3", condition nécessaire pour que la somme des chiffres soit
divisible par 3 et par 7. |
|||
|
Brèves associées |
>>>
Division
par 7 – Nombre 142 857 |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Semi-uniformes divisibles par leurs chiffres |
>>>
Nombres uniformes |
||
843. Chiffres en trous |
|
||
|
Quelle est la logique de ce tableau
?
Le nombre du
bas comptabilise la quantité de trous dans le nombre du haut. La suite de ces nombres RECORD à
partir de 0
|
|||
|
Brèves associées |
>>>
Plus grand nombre avec trois chiffres |
>>>
Brèves Énigmes – Index |
|
|
Pour en savoir plus |
>>>
Devinette des nombres à trous >>>
Jeux avec les nombres |
>>>
Humour 2022 |
|
844. Énigme des voitures |
|
|||
|
Énigme Quatorze voitures sont rangées l’une derrière
l’autre sur un parking. Toutes avec un numéro d’immatriculation différent, inférieur
à 1500. Chose étonnante, le numéro de chacune est égal à la somme des cubes
des chiffres du numéro de la voiture placée devant elle. Quel est le numéro de la première voiture ? Réponse par lecture de la liste ci-contre: 177. |
Cycle du cube des chiffres Chaque nombre du cycle est égal à la somme des cubes du précédent. 2 => 23 = 8 => 83 = 512 => 53
+ 13 + 23 = 134 => … Cycle de longueur 14 avec nombres différents: 177,
687, 1071, 345, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153. Arrêt à 153, car 13 + 53 + 33 = 153 Il existe un seul cycle plus grand qui part de 12 558, un nombre plus
grand que le 1500 de l'énigme. |
|||
|
Brèves associées |
>>>
Trois souris sur triangle |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Nombres narcissiques – Cycles |
>>>
Somme des chiffres |
||
845. Triangles de Conway |
|
||||||||||
|
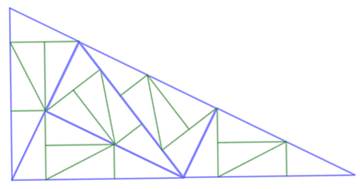
Triangle rectangle ABC partagé en 5
triangles isométriques Les côtés des cinq triangles sont dans un rapport d'homothétie = 1 /
racine de 5. En itérant le partage pour chaque petit triangle, on crée un pavage du
plan (Figure
de droite)
Calcul des dimensions
|
|||||||||||
|
Brèves associées |
>>>
Triangle de
Kepler (nombre d'or) |
>>>
Brèves Géométrie – Index |
|||||||||
|
Pour en savoir plus |
>>>
Triangle rectangle de Conway |
>>>
Racine de 5 |
|||||||||
846. Lettres devenues chiffres |
|
|||
|
En haut Nombres écrits avec une fonte à sept barres, comme sur les afficheurs
lumineux (calculette, par exemple). Particularité de pouvoir les lire comme des mots de la langue
française. En bas Amusement qui consiste à représenter une lettre par un chiffre ou un
symbole qui lui ressemble |
|
|||
|
|
||||
|
Brèves associées |
>>>
Nombre et ses chiffres |
>>>
Brèves Jeux – Index
|
||
|
Pour en savoir plus |
>>>
Lettres en chiffres |
>>> Jeux avec
les nombres – Index |
||
847. Numération en octal |
|
|||
|
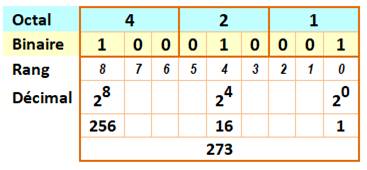
Octal Compter en octal consiste à compter avec huit chiffres (0, 1, … 7). Le
8 en décimal devient 10 en octal. Conversion en octal Elle est très pratique pour nommer du binaire: il
suffit de grouper les chiffres binaires (0 ou 1) par blocs de trois. Ainsi
010binaire devient 2 octal. Le tableau montre comment nommer ce nombre
binaire simplement par 421. La conversion de l'un en l'autre étant immédiate. La conversion hexadécimale offre la même
simplicité. |
27310
= 4218 = 100 101 0012
|
|||
|
Brèves associées |
>>>
Conversion en octal |
>>>
Brèves Numération – Index |
||
|
Pour en savoir plus |
>>>
Octal |
>>>
Hexadécimal |
||
848. Pépites numériques |
|
|||
|
|
|
|||
|
Brèves associées |
>>>
Pépites numériques (1) |
>>>
Brèves Motifs – Index
|
||
|
Pour en savoir plus |
>>>
Autre pétites en trapèze |
>>>
Pépites numériques |
||
849. Suites et méthode des différences |
|
|||||||||||||||||||||||||||||||||
|
Exemple avec la suite des cubes en
y Tableau des différences d'ordres successifs:
Pour les cubes,
la troisième différence est constante; c'est normal ! Pour la
puissance 10, ce serait la dixième différence. On retient les nombres de tête de ce tableau (en
jaune) pour effectuer nos calculs. |
Question Donner le douzième nombre de la série. Calcul La valeur est égale à la somme des nombres de
tête du tableau (en jaune), chacun étant pondéré par une sorte de coefficient
du binôme (en rouge).
Le nombre 1728 qui est bien le cube de 12. Pour la vingtième valeur, il suffit de remplacer
le 11 par 19 et suivre la logique pour les autres nombres en rouge: 1 + 19×7 + 171×12 + 969×6 = 8 000 = 203. La méthode
est très utile pour des cas moins communs que les cubes. Explications en
suivant le lien indiqué. |
|||||||||||||||||||||||||||||||||
|
Brèves associées |
>>>
Somme de cubes |
>>>
Brèves Calculs – Index |
||||||||||||||||||||||||||||||||
|
Pour en savoir plus |
>>>
Suites et méthode des différences |
>>>
Nombres 1728 |
||||||||||||||||||||||||||||||||
850. Ellipsographe |
|
|||
|
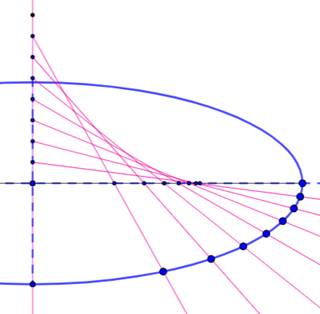
Construction de
l'ellipse Droite verticale et horizontale. Choisir k points équidistants sur
l'axe vertical à partir du centre (ici k = 8). Choisir une première longueur qui
sera maintenue constante pour construire les rayons joignant l'axe vertical à
l'axe horizontal. Les points sur l'axe horizontal sont irréguliers, c'est
normal. Choisir une seconde longueur qui
sera maintenue constante pour construire les points de l'ellipse sur chacun
des rayons Méthode laborieuse à la main, mais
facilement réalisable avec un outil appelé ellipsographe (ou trammel). Utile
pour les menuisiers et autres artisans. |
Méthode de
l'ellipsographe
Il existe d'autres méthodes plus
simples, mais toujours point par point.
|
|||
|
Brèves associées |
>>>
Construction du jardinier |
>>> Brèves
Constructions – Index
|
||
|
Pour en savoir plus |
>>>
Construction des ellipses |
>>>
Coniques |
||
851. Fractions et nombres entiers |
|
||
|
Voyez ces fractions
extraordinaires !
Ces fractions en 1/ (99…9k)2 engendrent
tous les nombres successifs jusqu'à 99…9k en omettant le nombre
juste précédent: 99…98. |
|||
|
Brèves associées |
>>>
Fractions
en boucle |
>>>
Brèves Opérations – Index |
|
|
Pour en savoir plus |
>>>
Fractions et nombres entiers |
>>>
Nombre de Lewis Carroll |
|
852. Infinité de premiers |
|
||
|
|
|||
|
Brèves associées |
>>>
Idem –
Plus d'infos |
>>>
Brèves Premiers – Index |
|
|
Pour en savoir plus |
>>>
Infinité de nombres premiers |
>>>
Euclide |
|
853. Problème de 18 points |
|
|||
|
Le problème Au final, on doit trouver cinq villas, une dans
chacun des cinquièmes de longueur; une dans chaque quart, une dans chaque
tiers et une dans chaque demi. La rue est représentée plusieurs fois pour
montrer l'appartenance à chaque fraction de longueur. L'impasse La distribution semble simple et sans limite.
Pourtant, si elle est encore possible avec 17 tronçons, elle est impossible
pour 18. Problème posé par le mathématicien polonais Hugo
Steinhauss en 1964. Prouvé en 1970. |
Pour k de 1 à 5, il y a exactement une villa dans
chaque tronçon de longueur 1/k. Pour k = 5, il y a 5 villas, une dans chaque
cinquième de longueur. |
|||
|
Brèves associées |
>>>
200 avec neuf chiffres |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Problèmes des 18 points |
>>>
Nombre 18 |
||
854. Compter les triangles |
|
|||
|
Combien
de triangles dans cette figure ? L'approche
consiste à compter les triangles seuls ou assemblés:
Total: 9
+ 5 + 6 + 5 + 2 + 0 + 1 + 1 = 29 |
|
|||
|
Brèves associées |
>>>
Triangulations des polygones |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Compter les triangles |
>>>
Points et triangles |
||
855. Règle des 72 |
|
|||
|
Méthode
pour estimer rapidement le doublement d'un placement, ou toute chose
croissante. La règle
des 72 est utilisée depuis la Renaissance (Luca Pacioli – 1494). |
Soit t le taux de croissance et T la durée en années (ou périodes) de la
croissance pour obtenir un doublement:
|
|||
|
Exemples Avec un taux de croissance de 1%, le doublement intervient en 72 ans
(environ; réalité: 69,3 ans). Avec un taux de croissance de 2%, le doublement intervient en 72/2 =
35,5 ans. Avec un taux de croissance de 10%, le doublement intervient en 72/10 =
7,2 ans. |
||||
|
Brèves associées |
>>> GAFAM
et trillion de dollars |
>>>
Brèves Économie – Index |
||
|
Pour en savoir plus |
>>>
Règle des 72 >>>
Intérêts simples ou composés |
>>>
Nombre 72 |
||
856. Divisibilité des factorielles |
|
|||
|
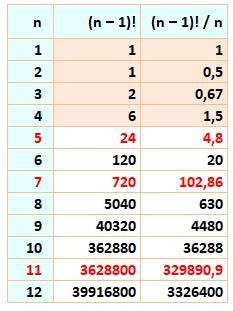
Propriété Voyons
une propriété plus simple que celle énoncée par le théorème de Wilson. On sait
évidemment que tous les nombres jusqu'à n divisent le nombre factoriel n. Mais,
est-ce que le nombre n divise la factorielle précédente (n – 1) ! ? Par
exemple, est-ce que 6 divise 5! = 1 x 2 x 3 x 4 x 5 ? La
réponse est toujours oui pour n supérieur à 4, sauf si le nombre n est
premier. Théorème Si n >
4 est composé alors n divise (n – 1)! |
Exemples
|
|||
|
Brèves associées |
>>> Divisibilité du produit de nombres |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Factorielle et théorème de Wilson >>>
Nombre premier |
>>>
Factorielles – Index
|
||
857. Quadrature du cercle |
|
|||
|
Les Anciens ont cherché à dessiner à la
règle et au compas un carré qui aurait la même aire que le cercle. Ils n'arrivaient qu'à des solutions approchées sans trouver la bonne. En 1882, Lindemann trouve le fin mot: la constante Pi est
transcendante (décimales diverses sans fin) et la construction est définitivement déclarée impossible. |
En 1925, Tarski propose une nouvelle piste: la dissection. Est-il possible de composer un carré et un cercle
de même aire en utilisant les mêmes pièces élémentaires. En 2002, après de nombreuses avancées, trois mathématiciens publient
une solution comportant plus de dix mille pièces. Ce sont des pièces qui ne peuvent pas être
découpées aux ciseaux; elles sont même non
mesurables ! |
|||
|
Brèves associées |
>>> Angle triple |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Quadrature du cercle |
>>>
Constructions géométriques – Index |
||
858. Construction brouette |
|
|||
|
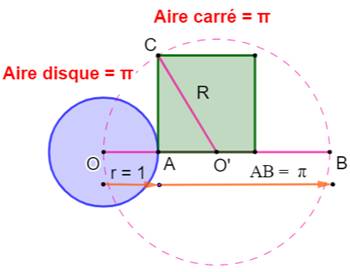
Comment
rapidement construire un carré ayant l'aire d'un cercle ? Construction Cercle de
rayon OA = 1. Prolonger OA tel
que AB = Pi . Milieu O' de AB. Cercle (O',
O'O). Perpendiculaire
AC en A à AB. Carré de côté
AC. Alors l'aire du
carré vaut Pi comme celle du disque. Remarque Ceci n'est pas
une construction à la règle et au compas. Elle nécessite la construction de
la longueur de Pi, ce qui est impossible. |
|
|||
|
Brèves associées |
>>>
Racine de n – Construction |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Constructions approchées de Pi |
>>> Valeurs
approchées de Pi |
||
859. Puissance 5 |
|
|||
|
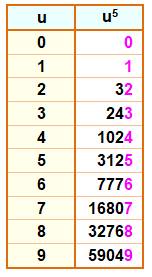
Théorème N et N5
ont la même unité. Même chose pour la puissance 9. Exemples 115 = 161 051
; 125 = 248 832 ; 135
= 371 293 Explications Identifions les unités: N = 10A + u À la puissance 5, tous calculs faits: N5
= 10B + u5 Or les chiffres à la puissance 5 se retrouvent en
unité. (Voir le
tableau) Pour information: le
développement de N5
|
|
|||
|
Brèves associées |
>>> Puissances des chiffres |
>>>
Brèves Motifs – Index
|
||
|
Pour en savoir plus |
>>>
Unité des puissances |
>>>
Puissances – Index
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()