|
|||||||||||||||||||||||||||
![]()
|
Nombres complexes ADDITION & SOUSTRACTION |
|
|
|||
|
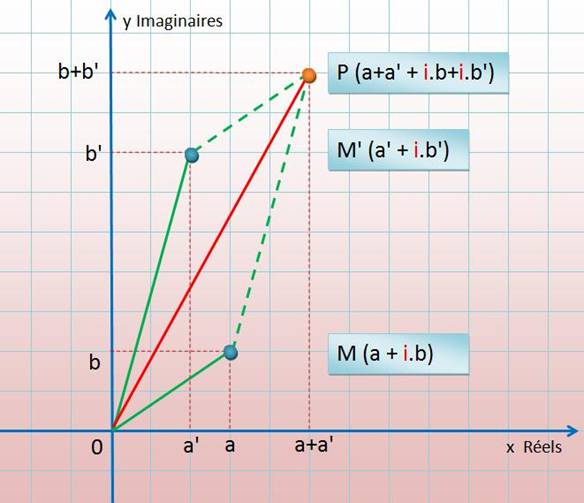
Opération |
(a + i.b)
+ (a' + i.b')
|
= a + a' + i (b + b') |
|
|
Représentation
géométrique |
|
||
|
Explications |
|
||
|
|
|||
|
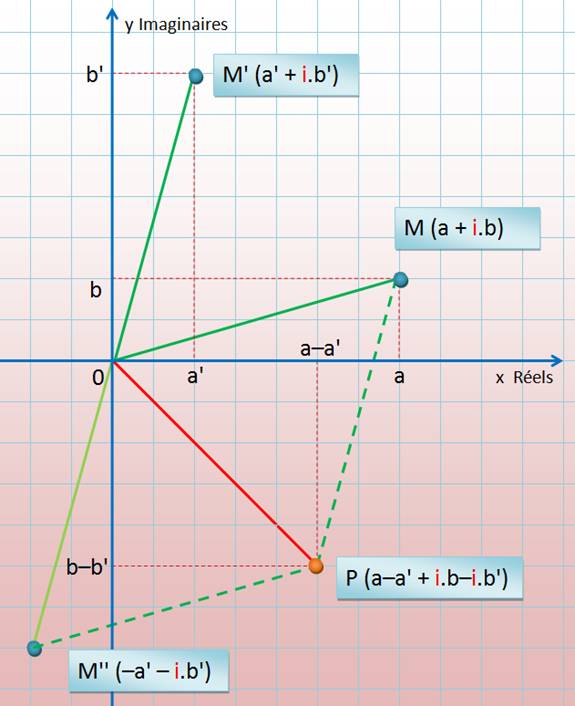
Opération |
(a + i.b)
– (a' + i.b')
|
= a – a' + i (b – b') |
|
|
Représentation
géométrique |
|
||
|
Explication |
(a + i.b) – (a' + i.b')
= (a + i.b) + (–a' – i.b')
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Addition.htm |
![]()