|
||||||||||||||||||||||||||||
![]()
|
Nombres complexes - DÉBUTANTS
Le nombre complexe, un outil indispensable
pour les électroniciens et tous ceux qui veulent modéliser les ondes. |
|
|
|
|
|
|
|
|
|
|
|
|
Attention
|
Les mathématiciens
n'aiment pas dire que i = racine de moins 1. Cette notation
étant bien commode, nous continuerons à l'utiliser, comme beaucoup le font.
Mémorisons simplement qu'il s'agit d'une notation pratique sans vouloir lui
faire dire autre chose. |
|
Nombres imaginaires |
|
|
Le principe est simple:
c'est la même valeur que pour le nombre positif, associé au nombre imaginaire
i.
|
|
|
Nombres complexes |
|
|
|
|
|
|
||
|
Addition Les réels avec les réels et les imaginaires avec les
imaginaires. |
|
|
|
Multiplication Règle habituelle du produit de polynômes, mais avec
l'effet de i² = – 1. |
|
|
|
Produit réel Cette multiplication de deux nombres complexes se
termine par un produit réel. Note: ces deux nombres sont appelés, l'un le conjugué
de l'autre. La notion de conjugué est fort utile pour effectuer les divisions de nombres complexes. |
|
|
|
Produits imaginaires Ces deux multiplications donnent des produits
imaginaires. |
|
|
|
|
||
|
|
|
|
Suite en Fractales
|
|
||
|
i2 = – 1 i3 = – i i4 = 1 |
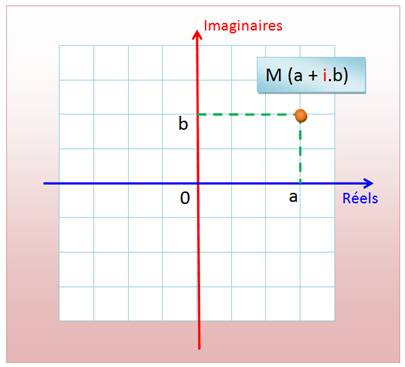
Affixe de M décrit de
deux façons:
|
|
Suite en Représentation
des nombres complexes / Puissance de l'imaginaire
/ Coordonnées
polaires
|
|
||
|
|
|
|
|
|
|
|
|
|
Il a
les nombres réels ![]() et les nombres complexes
et les nombres complexes ![]()

![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Debut.htm |
![]()