|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
||
|
Problème |
A
possède 7 chevaux asava B
possède 9 chevaux haya C
possède 10 chameaux Si chacun donne
un animal à chacun des deux autres, alors chacun possède la même richesse Quel est le prix
de chaque animal en nombres entiers
? |
|
|
Compréhension du problème |
|
|
|
Notations |
x
prix du cheval asaya y
prix du cheval haya z
prix du chameau V
richesse commune après don à chacun Le prix de l'ensemble
des animaux des trois personnes sera
ainsi égal à 3V |
|
|
Observation |
Si A
possède 7 chevaux, lorsqu'il en aura prêté 1 à B et 1 à C, il
lui en restera 5 en propre, mais il aura aussi reçu un cheval de B et un chameau de C; La richesse
commune est égale à la valeur des 5 chevaux qui reste à A, augmenté de
la valeur du cheval venant de B et du chameau venant de C Mêmes
observations pour B et pour C |
|
|
Illustration et équations |
|
|
|
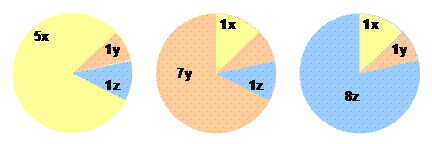
Illustration |
La
taille du cercle représente
la même richesse V
Chaque cercle
illustre de quoi est composée la richesse de chacun dont l'énoncé nous
indique qu'elle est la même |
|
|
Équations |
5x + y
+ z =
V x + 7y
+ z =
V x + y +
8z = V 7x
+ 9y + 10z = 3V |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Valeurs de x, y et z en fonction de V
Finalisation
Vérification
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()