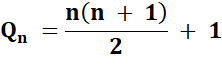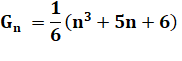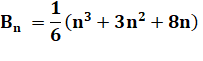|
||||||||||||||||||||||||||||
![]()
|
|
|
F |
Nombre / Dénombrement NOMBRES du traiteur paresseux Lazy caterer's sequence |
|
|
Approche |
Vous êtes
devant une tarte et disposer de 3 coups de couteaux. Combien de
parts de tartes pouvez-vous créer au maximum. Les parts ne sont pas égales
bien sûr. Problème
dit du cercle coupé par des droites. |
|
|
Définition |
Les
nombres polygonaux centrés (ou nombres du traiteur paresseux) indiquent la
quantité maximale de parts qu'il possible de découper dans une tarte. Les coupes
ne sont pas parallèles ni concourantes. |
Voir Calcul ci-dessous |
|
Exemples |
|
|
|
Propriétés |
Pour
passer d'un nombre au suivant, il suffit de lui ajouter n. Le énième coup de
couteau dégage n parts en plus. La suite
de ces nombres est la même que celle des nombres
triangulaires + 1.
|
|
Calcul
détaillé de Qn+1 - Qn
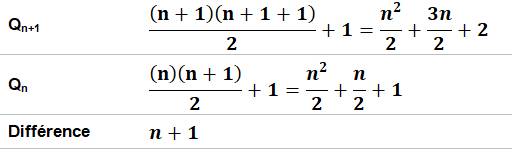
Merci à Jean-Marc Melchiore
pour ses remarques
|
|
|
|
Cette
simple instruction produit la suite
des cent premiers nombres polygonaux centrés. |
|
|
Cake
numbers – Potato numbers |
|
|
|
Quantité
maximum de régions obtenues par la découpe d'un cube par n plans. |
|
|
|
Illustration
pour n = 4; ce qui
donne 15 morceaux. Source
image: animation Wikipédia |
|
|
|
|
||
|
Anglais |
Central polygonal numbers; or The Lazy Caterer's sequence); or Maximal number of pieces formed when
slicing a pancake with n cuts. Cake numbers and space division of space. |
Illustration selon un triangle façon
triangle de Pascal
Les hexagones entourés montrent la façon
de calculer les nombres (16 = 11 + 5)
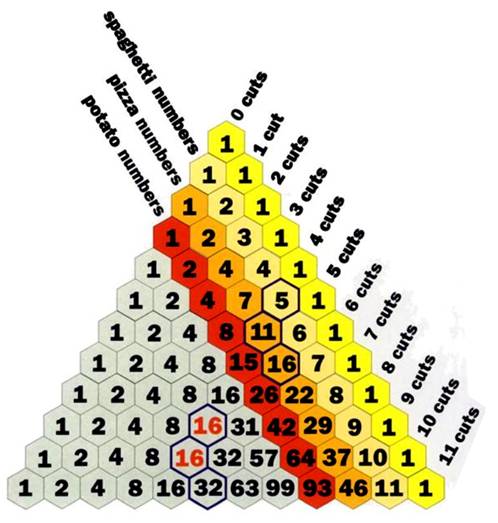
Source Image par Ivan Moscovich – Make a meal of this – Page 77
|
Chacune des neuf
personnes va pouvoir au moins y goûter. Certaines vont se régaler, d'autres
vont se retrouver sans grande possibilité d'y trouver la fève (parts 7, 8 et
9 au centre). Il est possible
d'atteindre 13 parts
avec trois coupes planes. Pas évident ! illustrations
Source image >>>
|
|
|
|||
|
Quantité
maximum de régions obtenues par la découpe d'un tore par n plans. |
|
||
|
Liste |
2, 6, 13, 24, 40, 62, 91, 128, 174, 23010,
297, 376, 468, 574, 695, 832, 986, 1158, 1349, 156020, 1792, 2046,
2323, 2624, 2950, 3302, 3681, 4088, 4524, 4990, 5487, 6016, 6578, 7174, 7805,
8472, 9176, 9918, 10699, 11520, 12382, 13286, 14233, 15224, 16260, 17342,
18471, 19648, 20874, 22150, … |
||
![]()
|
Suite |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()