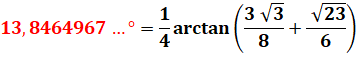Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 03/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	10	11		12	13		14	15	16	17	18	19

Nombre 13	Culture	Maths	Superstition 13
Expressions 13	Culture 13	Maths (suite)	Vendredi 13
Racine 13e	Sciences 13	Quantité 13	Tarot 13
Pluriels détournés		Géométrie et 13

Treize

Thirteen

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1101
Bases	1113 1112
Romain	XIII

Suite

13 = 2² + 3²

Voir 13 et la géométrie >>>

Caractérisation du nombre

Chanceux

Congruent

Coster

Déficient

Delannoy

Dichotomique et trichotomique premier

Docile (amenable)

Emirp (31 est premier)

Facteur fréquent

Fortuné

Fibonacci (7^e)

Heureux

Hofstadter – NON

Idonéal

Impair

Lucas (premier (rang)

Markov

Mersenne

Mian-Chowla

Modeste

Premier

Premier cubain

Premier de Bertrand

Premier de Chen

Premier de Pierpont

Premier de Pythagore

Premier de Wilson (2^e)

Premier faible

Premier jumeau avec 11

Premier permutable

Premier pointé

Premier régulier

Premier résistant

Premier supersingulier

Primeval

Proth

Tribonacci

Ulam

Carré centré

Hexagonal concentrique (3^e)

Nombre étoilé (2^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

Dans une file de 13 personnes, le dernier a un avantage sur le 7^e. En effet, lorsqu'il se retourne, il devient le premier. Tandis que quand le 7^e se retourne, il est toujours le 7^e – Geluck

Voir Pensées & humour

Numération – Chiffres – Dénombrement

1310 = 314 3110 = 1328		Exactement les mêmes chiffres en base 4. Le plus petit cas. Même chose avec son retourné.
1310 = 216 = 1211		Mêmes chiffres dans deux bases différentes.
13 et 31 sont premiers		Premier Circulaire (ou absolu). Tous deux contenus dans le début de Pi. (de tels nombres sont rares!). Nombre de Wilson premier.
13 + 1 + 3 = 17		Le nombre ajouté à ses chiffres pointent vers le nombre premier suivant.
3, 13, 31 sont premiers		Nombre multi-premier. Voir Brève 760
13 premier 15 = 3 x 5 semi premier		Nombre premier de Chen.
13 = 1 + (1+ 3) x 3		Plus petit nombre de Coster (hors 0 et 1). Égal à des opérations simples utilisant deux fois ses chiffres.
13 => 1 + 3 = 2²		Le plus petit premier dont la somme des chiffres est un carré.
13 = (1 x 3) + (1² + 3²) 13 = (1² x 3²) + (1 + 3)		Nombre somme-produit.
Pi = 3,1415926535897…		Avec 13 décimales (14 chiffres), la constante Pi contient tous les chiffres de 1 à 9.
13 x 4 = 52		Nombres de semaines dans l'année.
13 = QA(10^5)		Quantité de paires amiables jusqu'à 10^5.
13	Il existe 13 façons de classer trois éléments en suites ordonnées.

Addition – Partition

p(13) = 101	Quantité de partitions du nombre.
13 = 5 + 8 = 2 + 4 + 7	Fibonacci (7^e) et Tribonacci.
13 – 4 = 9 13² – 4² = 153 13^3 – 4^3 = 2133 …	Motifs produisant une persistance avec des carrés et des cubes.

Multiplication – Division

13	Inconsommable en binaire. Le plus petit. Aucun nombre k divisé par la somme de ses chiffres ne donne 13.
13 mod 3 = 1		Plus petit nombre modeste: on retrouve tous ses chiffres dans cette opération.
13 x 62 = 31 x 26 = 806 13 x 93 = 31 x 39 = 1 209 26 x 93 = 62 x 39 = 2 418		Produits avec retournement.
2 × 3 × 5 × 7 × 11 × 13 – 1 premier			Primorielle – 1 première.

Division rapide par 13

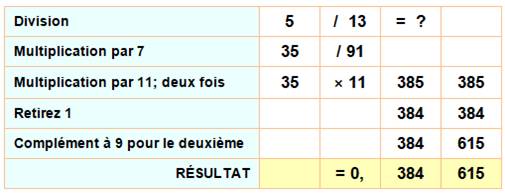
Du fait que 13 x 7 = 91, on peut se ramener à une division par 91 en multipliant tout par 7.

Voir Brève 568 / Divisibilité par 91

	Clé de divisibilité par 13. Constituer des blocs de 3 chiffres. les additionner et soustraire alternativement. Le résultat doit être divisible par 13
k | (n² + 3) & (n + 1)² + 3 alors k = 5	Si un nombre divise à la fois ces deux expressions, alors ce nombre est 13. Exemples ci-dessous.
13 = 223 – 210	Nombre fortuné: différence entre primorielle et le premier juste plus grand (d'au moins 2).

Exemples

Voir Brève 47-932 / Nombre 5 pour propriété identique

13 => 3, 11, 13, 17, 19, 23, 43, 53, 73, 83				Le nombre 13 engendre dix nombres premiers en modifiant un de ses deux chiffres. Suivant 101 avec 11 cas
13 = (4! + 2!) / 2! 31 = (6! + 4!) / 4!				Division avec des factorielles.
13 est le 6^e nombre premier alors que 6 = 1! · 3! 226130351 est le 12441600^e qui vaut 2!·2!·6!·1!·3!·0!·3!·5!·1!					Curiosité avec le produit des factorielles et son suivant.
76 + 923 = 999 7 + 69 + 23 = 99				Développement décimal de période 6 et avec deux types de décimales: {0, 2, 3, 6, 7, 9}, {1, 3, 4, 5, 6, 8} Le nombre 13 est dichotomique et trichotomique premier; les demi-périodes de 1/13, comme ses tiers de période, somment en nombres en 9. La période multipliée par les nombres de 1 à 12 produit deux cycles de permutations. Multipliée par 13, on obtient un 9-repgigit. En effet, avec une seule période: 0,076923 x 13 = 9,99999.
1 / 13 = 0,076923 07… 2 / 13 = 0,153846 15… 3 / 13 = 0,230769 23… 4 / 13 = 0,307692 30… 5 / 13 = 0,384615 38… 6 / 13 = 0,461538 46… 7 / 13 = 0,538461 53…		8 / 13 = 0,615384 61… 9 / 13 = 0,692307 69… 10 / 13 = 0,76923 07… 11 / 13 = 0,846153 84… 12 / 13 = 0,923076 92… 13 / 13 = 1						Toutes les fractions avec 13 au dénominateur possèdent 6 décimales répétitives en deux suites permutées: [0, 7, 6, 9, 2, 3] ou [1, 5, 3, 8, 4, 6] .
abcabc est divisible par 13						Voir Nombres répétés
13 p^12 – q^12			Divisibilité par 13 si p ou q non divisibles par 13.
13 (1^k + 2^k + 3^k + 4^k + 5^k + 6^k) avec k = 4n + 2 Ex pour n = 1: 1 + 64 + 729 + 4096 + 15625 + 46656 = 67171 = 13 x 5167							Le nombre 13 divise toujours cette somme de puissances
	Le nombre de classe de ce corps quadratique est 2. Ce corps contient tous les nombres de la forme a + ib avec a et b rationnels. Il existe 18 tels corps avec k = 5, 6, 10, 13, 15, 22, 35, 37, 51, 58, 91, 115, 123, 187, 235, 267, 403, 427. OEIS A005847 / Table

Avec des puissances

13 => 1² + 3² = 10 et 1² + 0² = 1		Cycle des carrés
1 + 2 + 3 + … + 13 = 1² + 2² + 3² + 4² + 5² + 6²		La somme des nombres de 1 à 13 est égale à la somme de carrés consécutifs. Seuls cas: (1, 1), (10, 5), (13, 6) et (645, 85).
13 – (1 + 3) = 3² 13 + (1 x 3) = 4²		Curiosité avec ses chiffres.
13 = 2² + 3² = 1² + 2² + 2² + 2² = 1² + 1² + 1² + 1² + 3²		Seule somme de carré >>> Somme des carrés de nombres consécutifs. Nombre carré centré. Nombre binomial. Trois fois somme de n carrés, n 5. Voir Somme carrés / Autour de 12345
13 = 17^3 – 70² = 4913 – 4900		Seul cas d'équation de Bachet pour k = 13. Différence entre un cube et un carré.
13 = 3^0 + 3^1 + 3^2		Somme puissances successives.
13 = 1^2 + 2^2 + 2^3		Somme cumulée des puissances pures jusqu'à 8 = 2^3.
13 = 7² – 6² = 7 + 6		Différence de deux carrés de nombres consécutifs, comme tous les nombres impairs. Motif général.
		Différence entre puissances.
13 = 4² – 4 + 1	Nombre polygonal centré d'ordre 2 ou nombre de Hogben.
7² + 120 = 13² et 13² + 120 = 17²		Carrés en progression arithmétique et nombres congruents.
13 = (3^3 – 1^3) / 2 = (27 – 1) / 2		Premier nombre premier cubain d'ordre 2.
= 0,2962962963… + 12,70370370…		Sommes de deux cubes rationnels.

Puissance du nombre

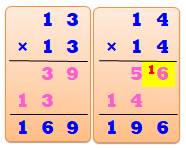
13² = 169 14² = 196 31² = 961			Les carrés de 13 et 14 sont des anagrammes. Nombre fluet: carré obtenu sans occasionner de retenue lors de la multiplication. Ce n'est pas le cas pour 14 avec 4 x 4 = 16. Nombres fluets inferieurs à 100: 1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 30, 31. Voir 157
13² = 169 103² = 10609 301² = 90601 31² = 961 130² = 16900 103² = 10609 (1 + 3)² = 1 + 6 + 9 = 16				Motifs palindromiques: le carré de son symétrique est le symétrique de son carré; le carré de la somme de ses chiffres est égal à la somme des chiffres de son carré. Même motif avec 12.
13² = 169 31² = 961				Nombre carrément réversible: les carrés des retourné sont retournés.
13^2= 12 ² + 5² = 144 + 25 = 169		L'écart entre 13 et 12 au carré est un carré. 2^e Triplet de Pythagore. 2^e avec hypoténuse = côté -1
13² = 3² + 4² + 12²		Seule somme de trois carrés distincts.
13² = 169 14² = 196		Chiffres inversés. Voir Motif avec 149
13^2 = 169 & 1 + 6 + 9 = 16 16² = 256 & 2 + 5 + 6 = 13		Motif en couple.
13² x 31² = 403² = 169 x 961 = 162 409		Motif avec double retournements.
13^3 = 9² + 46² = 26² + 39²		Cube somme de deux carrés.
1^3 + 3^3 = 28 2^3 + 8^3 = 520 5^3 + 2^3 + 0^3 = 133 1^3 + 3^3 + 3^3 = 55 5^3 + 5^3 = 250 2^3 + 5^3 + 0^3 = 133		La suite narcissique du 13 se termine par le cycle 133, 55, 250. 13 et 133: les ésotéristes y voient une signification
13^5 + 16^5 = 17^5 + 12 13 + 16 = 17 + 12		Presque-Fermat avec coquetterie.
…u^13 = … u		La puissance 13^e d'un nombre quelconque se termine par le même chiffre des unités que le nombre lui-même.
13^4 = 119² + 120²		Somme de puissances.
2^13 = 81 92 (8 + 2 = 9 + 1 = 10) Liste de telles puissances [13, 10], [43, 28], [47, 34], [51, 40], [126, 86], [194, 128], [386, 272]		Égalité entre somme des chiffres pairs et somme des chiffres impairs. Ces seules (?) sept puissances de 2 partagent la même propriété. Le deuxième nombre est la somme commune des chiffres.
2^13 = 8192 => 1289		Le nombre formé par les chiffres rangés par ordre croissant est un nombre premier.

Autour du nombre

13 et 31 26 et 62	Palinquad: couple de nombres et leur double palindromes.
1! + 2! + … + 7! = 5 913	Toutes les sommes de factorielles à partir de là se terminent par 13.
2^13 = 8 192	La somme des chiffres pairs est égale à celle des chiffres impairs.
2^13 – 1 = 8 191	Cinquième nombre de Mersenne premier.
M(13) = –3	La fonction de Mertens atteint –3 pour la 1^ère fois.

Dénombrement, jeux et curiosités

13 = 11 + 2 = 12 + 1		Eleven + two = twelve + one: anagramme
13 = 9 + 3 + 1 = 1 + 8 + 4 = 4 + 7 + 2 = 2 + 5 + 6		Escalier numérique (jeu) >>>
77 = 13 + 8x8 717 = 13 + 8x88 7117 = 13 + 8x888 …		Motif itératif
		Jeu du quatre 4.
		Comment écrire 13 avec des puissances de 4.
		Mêmes chiffres de part et d'autre de l'égalité.
13, 18, 63, 27, 45, 90, 81, 63, 27, 45		Algorithme de Kaprekar le plus petit maximum à deux chiffres.
13, 14, 15, 84	Côtés et aire d'un triangle héronien.
	Nombre maximal de morceaux obtenus en sectionnant un tore par trois plans. OEIS A003600 Source image: Clifford Pickover

Décimales

13,39 … = 100 (1 – ) = 13, 39745 96215 56135 32362 …	Rapport de Steiner.
	Demi-angle au centre du tridécagone régulier (13 côtés).
	Très bonne approximation de Pi/13.
	Angle de la semi-médiane du triangle équilatéral. Valeur approchée de Pi/13

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 0, 1] 3, [1, 1, 1] 4, [3, 1] anagramme 5, [2, 3]	6, [2, 1] 7, [1, 6] 8, [1, 5] 9, [1, 4]	10, [1, 3] 11, [1, 2] 12, [1, 1] 13, [1, 0]	3, [1, 1, 1] 12, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombre 13 en maths (suite)
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/TreizeNb.htm