NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/09/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Physique
Débutants Général	TROIS CORPS	Glossaire Unités
INDEX Sciences	Sommaire de cette page >>> Le problème des trois corps >>> Prix >>> Problème résolu par simulation (2017) >>> Vers une idée de la solution (2019)

Le problème des TROIS CORPS

La mécanique céleste commence à être très compliquée à partir de trois objets!

Le problème des trois corps

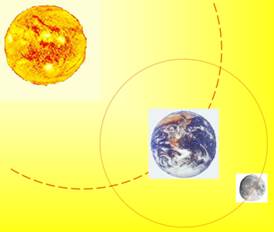
Newton (1642 - 1727) avec sa théorie de l'attraction universelle donne la formule du mouvement des planètes. Mais ces formules, aussi puissantes soient elles, ne permettent pas de calculer précisément le mouvement de seulement trois objets, compte tenu de leurs influences mutuelles. (Newton vers 1680). C'est le Problème des trois corps Exemple: Soleil / Terre / Lune. L'orbite d'une planète est influencée majoritairement par le Soleil, mais son orbite n'est pas une ellipse parfaite. La trajectoire de la planète est aussi influencée par les autres corps célestes présents. les calculs pour un astre attiré par un autre est maîtrisé. Qu'en est-il pour trois et pus? Le problème est extrêmement complexe déjà pour trois corps et, inextricable pour le système solaire complet. C'est le mathématicien français Lagrange (1736 - 1813) qui ira le plus loin à l'époque de la révolution française. Il établi un système de douze équations. Ce n'est pas la solution, mais un pas précieux pour ses successeurs. Euler, lui-aussi, contribua aux recherches. Hamilton et, surtout, Poincaré ont poursuivi la tâche. Poincaré montre notamment qu'il n'y a pas de solution analytique à ce problème des trois corps. Pour progresser, il avait supposé trois corps de tailles très différentes: un très gros (le Soleil), un moyen (la Terre) et un tout petit (la Lune). Aujourd'hui, les solutions sont recherchées par simulation sur ordinateurs avec – surprise! – prévision de systèmes qui pourraient devenir chaotiques! Est-ce que la Terre, un jour, pourrait décrocher de son orbite? Dans les années 1970, le mathématicien américain Roger Broucke et l'astronome français Michel Hénon ont découvert d'autres solutions. Alors, les solutions spécifiques pouvaient être classées en trois familles: la famille Lagrange-Euler, la famille Broucke-Hénon et la famille en huit (solutions en forme de huit), dont la dernière a été découverte en 1993 par le physicien Cristopher Moore de l'Institut de Santa Fe. En 2023, la découverte de treize nouvelles familles, faite par les physiciens Milovan Šuvakov et Veljko Dmitrašinović de l'Institut de physique de Belgrade, porte le nouveau total à 16 familles de solutions.

Prix Oskar

En 1889, le roi Oskar II de Suède souhaite fêter son anniversaire. Le mathématicien Gösta Mittag-Leffler propose la création d'un prix au meilleur mémoire sur le problème des n corps, l'un des trois sujets proposés. Le mathématicien Weierstrass formule le problème posé: Étant donné un système de n corps qui s'attirent mutuellement conformément à la loi de la gravitation, et en supposant qu'il n'y ait jamais de collision entre deux corps, donner les coordonnées des corps individuels, pour n'importe quel moment de l'avenir ou du passé, sous la forme d'une série uniformément convergente dont les termes sont composés de fonctions connues. Extrait de La conjecture de Poincaré – George Szpiro –– JC Lattès Parmi les douze mémoires présentés, aucun n'avait la solution. Le prix fut accordé à Poincaré pur ses travaux remarquables sur la dynamique des corps en mouvement.

Problème résolu par simulation (2017)
Le problème astronomique des "trois corps" possède des centaines de solutions. Des chercheurs chinois ont dévoilé 695 puis 1223 solutions au problème, alors que seules 13 avaient été exhumées jusque-là. (Université de Shanghai Jiaotong en Chine) Algorithme novateur, dit clean numerical simulation (CNS), conçu en 2009 par l'un des chercheurs, et au supercalculateur Tianhe-II (le plus puissant du monde), les chercheurs ont trouvé des centaines de configurations initiales entre trois corps conduisant le système à retrouver (au bout d'un temps qui peut être long) cette configuration, et donc à répéter indéfiniment le même cycle (sans collisions). Anglais: Infamous three-body problem has over a thousand new solutions.

Vers une idée de la solution (2019)
Grand pas en 2019 vers la résolution de cette vieille énigme par une équipe dirigée par des chercheurs de l'université hébraïque de Jérusalem. Elle a développé une méthode statistique de travail qui pourrait tout de même s'avérer d'une grande utilité.	Les chercheurs se sont appuyés sur des travaux qui suggèrent que, dans un système à trois corps instable et chaotique, l'un des corps finit toujours par être expulsé. Il en résulte une relation binaire entre les deux corps restants.

Suite: Vers une solution pour le problème à trois corps – Nathalie Mayer – 31/12/2019 – Futura Sciences

Suite	Gravitation Les cinq points de Lagrange Le problème des trois corps – Roman de Liu Cixin
Voir	Trigonométrie Équations différentielles
Aussi	DicoCulture
DicoNombre	Nombre 3 Nombre 12
Site	Vers une solution pour le problème à trois corps – Nathalie Mayer – Futura Sciences – 2019 L’anneau d’Henri Poincaré – Marie-Claude Arnaud, Patrick Massot –CNRS – 2012
Cette page	http://villemin.gerard.free.fr/aScience/Physique/TroiCorp.htm