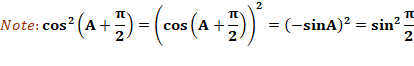|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Le point animé sur le cercle et relations avec le sinus et le
cosinus
|
|
|
TRIGONOMÉTRIE
Pourquoi avoir
inventé cette branche des maths ? Comment s'en servir ? Les noms compliqués
de sinus, cosinus, tangente
sont des noms de baptême qui ne doivent pas effrayer! Ils donnent le
moyen de calculer la longueur d'un côté d'un triangle rectangle. Ce sont les
rapports entre les côtés et l'hypoténuse en fonction de l'angle. |
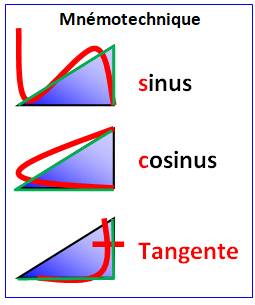
Voir Mnémotechnique
/ Les trois lignes:
sinus; cosinus et tangente
|
Cité
par Bruno Winckler |
Voir
Pensées & humour
|
|
|||||||||||||||||||||
|
Général
Angles
Unités Lignes
trigonométriques – Définitions et valeurs
Outils
trigonométriques – Identités, formules
Calculs
niveau Troisième Calculs
niveau Première
Usage
Géométrie
|
|||||||||||||||||||||
![]()
Introduction à la trigonométrie
|
|
|
|
|
|
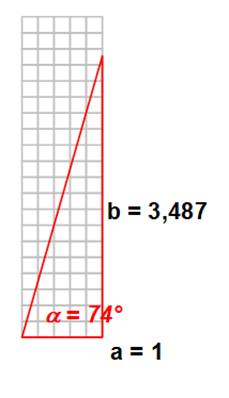
Prendre la tangente …
|
Données
Question
Réponse
b
= 3,487 414 44 …
b
= 3,487 414 443 840 908 650 4… En pratique
C'est la tangente.
Exemple de calcul Prenons 74° Sa tangente est 3,487… C'est le modèle
de référence, avec a = 1 Si a est dilaté par 15 Le côté b le sera aussi a = 15 => b = 3,487 x 15 = 52,305… |
|
Voir Initiation aux
dérivées / Angle apparent de la Lune
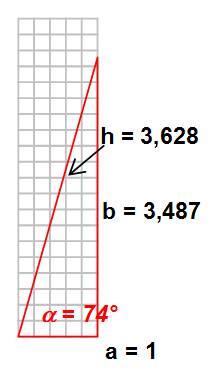
Professeur nimbus… et l'hypoténuse?
|
Données
Question
Réponse
Exemple de calcul Prenons 74° cos (74°) = 0,2756 ... Si a vaut 1, alors h = a / cos (74°) = 1 / 0,2756 =
3,628… Si a est dilaté par 15 L'hypoténuse le sera aussi: a = 15 => h = 3,628 x 15 = 54,42 |
|
|
|
||
|
|
||
|
COSINUS et cosécante
SINUS et sécante
|
TANGENTE
La tangente est aussi le rapport du sinus
au cosinus; donc le côté éloigné est au numérateur:
COTANGENTE
|
|
|
ARCSIN, ARCCOS …
On écrit:
Arcsin(x) = angle Arcsin(1) = Pi/2 =
90° Accès avec
la calculette, en
cliquant sue la touche 2nd |
Accès aux valeurs
trigonométriques par la calculette
Vous pouvez aussi taper simplement
sin(50) dans le moteur de recherche et la réponse sera 0,766 |
|
Voir
Valeurs
principales / Tables
et graphique / Arctangente
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
Avec notre triangle rectangle
dont l'angle vaut 74 °
Exemples a = 15 => b = 3,487 x 15 =
52,31… h = 15 => b = 0,961 x 15 =
14,415… h = 15 => a = 0,2756 x 15 =
4,134 … Il est possible d'utiliser
les formules à l'envers b = 15 => a = 15 / 3,487 = 4,30… b = 15 => h = 15 / 0,961 = 15,60… a = 15 => h = 15 / 0,2756 = 54,42… De base, vous l'avez
compris, il est possible de calculer l'angle b = 15
et a = 52, 31 => tan( Pour le fun, les valeurs
ci-dessus avec 20 chiffres Valeurs
trigonométriques pures Valeurs des exemples (avec 15) tangente 3,
4874144438409086504 52,
311216657613629756 sinus 0,
9612616959383188619 14,
418925439074782929 cosinus 0, 2756373558169991856 4, 134560337254987785 1 / tg 0,
2867453857588079400 4, 301180786382119101 1 / sin 1,
0402994358616020971 15,
604491537924031456 1 / cos 3,
6279552785433000973 54,
419329178149501460 |
||||||||||||||||||||||||||||||||||||
|
Arad Exemples A = 0,1 radian: sin(A) = 0,0998; tan(A) = 0,1003 A = 0,01 radian: sin(A) =
0,0099998; tan(A) = 0,0100003 |
Voir Angle
apparent de la Lune / Radian
|
|
||
|
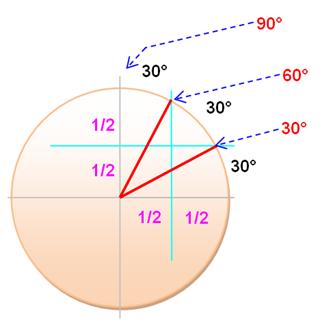
sinus
30° = ½ cosinus 60° = ½ Notez que sinus 60° =
|
|
|
Voir
Construction des angles de 30°
et 60° / Autres valeurs / Secteurs de disque /
Constructions géométriques des nombres / Partage du cercle
|
Les seules
valeurs rationnelles
des angles du premier quadrant telles que le sinus soit aussi rationnel sont:
0°, 30° et 90°.
|
Voir Nombre
0,5
|
|
||
|
La somme des carrés du sinus
et du cosinus vaut 1. |
|
|
|
Application:
calculer E
|
||
Voir Formulaire / Exemple de calcul
avec cette identité / Cas en
3D
|
|
|||
|
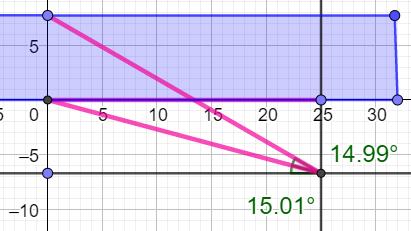
Énoncé Rivière
de largeur inconnue x. Relevé au
sol selon le croquis. Largeur
de la rivière ? Calculs
Calcul exact
|
|
||
|
Vérification avec le |
|
||
|
|
|
|
Tablette
découverte au début des années 1900 dans le sud de l'Irak par Edgar Banks, un
archéologue et diplomate qui a inspiré le personnage d'Indiana Jones.
Voir D; Knuth découvre l'aspect algorithmique
des calculs babyloniens
Sans
doute antérieure à Plimpton 322, mais déchiffrée plus tard (publication en
2021). Publication
en 2022 dans Fondements des sciences. Relative
à l'arpentage: plans utilisés par les géomètres pour définir les limites des
terres. Détermination
des angles droits à l'aide de triplets de Pythagore, mille ans avant la
naissance de Pythagore.
|
|
La
dérivée d'un sinus est le cosinus
L'intégrale
d'un sinus est un cosinus

Voir Dérivation
et intégration
|
Suite en |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()