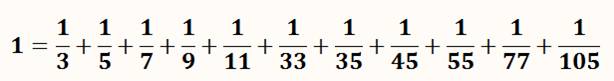fractions - somme égale à un

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/04/2018 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Type de nombres
Débutants Fraction	FRACTIONS de somme égale à 1			Glossaire Fraction
INDEX Calcul	Approche	Exploration	Ordres 2, 3 & 4
	Plus petite fraction	Propriétés	Ordre 5
	Nombres bons	Jusqu'à 100	Ordre 6
	Sommaire de cette page >>> Simplement >>> Unique >>> Impair >>> Premier >>> Combinaisons

FRACTIONS

Somme = 1

Différents types de nombres bons.

Rappel:

La somme des inverses des termes d'une de ses partitions est égale à un.

*Simplement*	S – Bon	Aucune contrainte sur les termes
*Unique*	U – Bon	Chaque terme est unique, jamais répété
*Impair*	I – Bon	Les termes sont tous impairs
*Premier*	P – Bon	Les termes sont tous Premiers

S est la somme des nombres formant la partition; Autrement-dit: des dénominateurs des fractions.

SIMPLEMENT

Pour toute somme S, il est possible de trouver au moins un nombre S-Bon, sauf 14 petits nombres:

à partir de 25, ils sont tous S-bons.

à partir de 27, ils sont tous doublement S-bons.

Le nombre 100 est 136 fois S-bon.

UNIQUE

Les U-Bons sont ceux dont la partition ne comprend que des nombres différents.

Voici les 7 U-bons jusqu'à l''ordre 4:

n	a	b	c	d
11	2	3	6
24	2	4	6	12
30	2	3	10	15
31	2	4	5	20
32	2	3	9	18
37	2	3	8	24
54	2	3	7	42

Exemple avec 100:

100

Propriété

Tout nombre supérieur à 23 est bon, mais tout nombre supérieur à 77 peut être décomposé en une somme d'entiers distincts dont la somme des inverses est égale à l'unité.

Graham 1963

Exemple

78 = 2 + 6 + 8 + 10 + 12 + 40

IMPAIR

Impairs Bons

On peut partitionner le nombre 1 en fractions impaires dont certaines sont répétées:

1 = 1/3 + 1/3 + 1/3

1 = 1/3 + 1/3 + 1/5 + 1/15 + 1/15

1 = 1/3 + 1/5 + 1/5 + 1/5 + 1/15

1 = 1/5 + 1/5 + 1/5 + 1/5 + 1/5

1 = 1/3 + 1/5 + 1/5 + 1/7 + 1/9 + 1/80 + 1/5040

Quelques autres exemples

1 = 2/3 + 1/5 + 1/9 + 1/45

1 = 6/7 + 1/9 + 1/33 + 1/693

1 = 8/9 + 1/11 + 1/51 + 1/1683

1 = 12/13 + 1/15 + 1/99 + 1/6435

Il s'agit des présentations pour lesquelles la première fraction est la plus grande pour un nombre impair donné, comme 8/9 ou 12/13.

Impairs et Uniques Bons

Seule façon de partitionner 1 en somme d'inverses impairs différents inférieurs à 1/105.

Autre manière, moins de fractions, mais supérieures à 1/105

Voir Nombre 105 / Nombre 1

PREMIER

1 = 1/2 + 1/2

1 = 1/3 + 1/3 + 1/3

1 = 1/5 + 1/5 + 1/5 + 1/5 + 1/5

1 = p fois 1/p

Toutes les présentations en p fois 1/p donne évidemment des nombres P-bons. Ce sont dons les carrés des nombres premiers.
Je ne connais pas d'autres nombres P-bons.

COMBINAISONS
Impair-bon	Unique-bon		Exemples
X			1 = 1/3 + 1/3 + 1/3
	X		1 = 1/2 + 1/3 + 1/6
X	X		1 = 1/3 + 1/5 + 1/7 + … ci-dessus
		Premier-bon
		X	1 = 1/2 + 1/2
X		X	1 = 1/3 + 1/3 + 1/3
	X	X	?
X	X	X	?

Suite	Jusqu'à 100
Voir	Divisibilité Fractions Fractions continues Fractions égyptiennes Multiplications Multiplications magiques Nombre et répétition de motifs Rep-Unit Table des fractions égyptiennes Nombres semi-parfaits primaires
DicoNombre	Nombre 1 Nombre 23 Nombre 77
Cette page	http://villemin.gerard.free.fr/Calcul/Fraction/Pde1a100/Fr1nbbon.htm