NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/07/2023 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Type de nombres
Débutants Fraction	FRACTIONS de somme égale à 1			Glossaire Fraction
INDEX Calcul	Approche	Exploration	Ordres 2, 3 & 4
	Plus petite fraction	Propriétés	Ordre 5
	Nombres bons	Jusqu'à 100	Ordre 6
		Sommaire de cette page >>> Approche >>> Mise en bouche >>> Nombres bons >>> Avec deux fractions >>> Avec trois fractions >>> Bons & parfaits

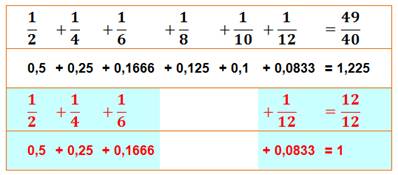
FRACTIONS

Somme = 1

Exemples (avec somme des dénominateurs à droite):

1 =	1/2 + 1/2	4
	1/2 + 1/3 + 1/6	11
	1/2 + 1/3 + 1/7 + 1/42	54
	1/2 + 1/3 + 1/7 + 1/78 + 1/91	181
	…

Il en existe une infinité.

La somme des dénominateurs donne un nombre (4, 11 …).

Peut-on obtenir tous les nombres de la sorte ?

Non ! Les heureux élus sont les nombres bons.

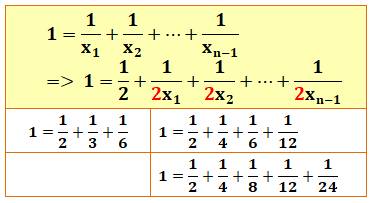
Procédure pour obtenir une infinité de sommes égales à 1

en utilisant la relation indiquée en jaune.

Quelques exemples. En rouge les fractions remplacées.

Voir Nombre 1 / Brève 51-1012

Une autre méthode très simple

APPROCHE
Peut-on trouver une solution à l'équation => Même question avec trois fractions => Et avec 4, 5 … ? À partir de trois fractions, il existe de nombreuses configurations. Comment les caractériser? Pourquoi pas, par la somme des dénominateurs.	1 = 1/a + 1/b Aucune avec a et b différents. La seule solution est a = b = 2. 1 = 1/a + 1/b + 1/c Oui! 1 = 1/2 + 1/3 + 1/6 On note: (2, 3, 6) Suivants: (2, 3, 7, 42) >>> (3, 4, 5, 6, 20) >>> (3, 4, 6, 10, 12, 15) >>> …

Voir Visualiser les fractions

Mise en bouche – Somme de fractions
Somme des premières fractions paires. Dont une combinaison donne la somme 1.
Somme limite égale à 1 pour n tendant vers l'infini. Propriété. En reprenant la première formule et en remplaçant. Les fractions adjacentes s'éliminent deux à deux.	La fraction 1/(n+1) tend vers la valeur 0 lorsque n tend vers l'infini, et la somme tend vers 1.

Voir Fractions en 0,5

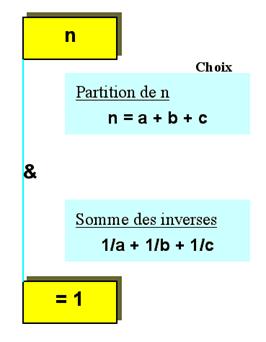
NOMBRES BONS

Nombres bons

Un nombre bon est un nombre qui ayant une partition, la somme des inverses des termes de la partition est égale à 1.

n = a + b + c + … 1/a + 1/b + 1/c + … = 1

Exemples

4 = 2 + 2	1/2 + 1/2 = 1
11 = 2 + 3 + 6	1/2 + 1/3 + 1/6 = 1
25 = 5 + 5 + 5 + 5 + 5	1/5 + 1/5 + 1/5 + 1/5 + 1/5 = 1

Problème équivalent

Les fractions avec numérateur unité sont dites fractions unitaires

Trouver toutes les combinaisons de fractions égyptiennes donnant une somme égale à 1.

Types de nombres bons

Simplement	S – Bon	Aucune contrainte sur les termes.
Unique	U – Bon	Chaque terme est unique, jamais répété.
Impair	I – Bon	Les termes sont tous impairs.
Premier	P – Bon	Les termes sont tous Premiers.

Voir fractions égyptiennes / Nombres bons / Trois fractions uniatire

AVEC DEUX FRACTIONS

La plus grande fraction est bien évidemment ½. La valeur 1 est obtenue avec deux fractions ½.
Si on tente d'associer la plus grande 1/2 à la suivante, plus petite, 1/3, on ne peut plus atteindre la valeur 1.

À noter: multiplication

On peut formuler le problème sous la forme indiquée ci-contre.
Trouvez les nombres ayant cette propriété.

1/2 + 1/2	= 1	& 2 + 2 = 4
1/2 + 1/3	= 5/6	inférieure à 1

4 est un nombre bon

et c'est le seul utilisant 2 fractions.

1/a + 1/b = 1

b + a = a.b

Seul 4 = 2 x 2
possède cette propriété.

AVEC 3 FRACTIONS

Les nombres 9, 10 et 11 sont des nombres bons d'ordre 3.

Seuls 9, 10 et 11 acceptent une partition ayant cette propriété.

1/2 + 1/3 + 1/6	= 1	2 + 3 + 6 = 11
1/2 + 1/4 + 1/4		2 + 4 + 4 = 10
1/3 + 1/3 + 1/3		3 + 3 + 3 = 9

Deux relations équivalentes

1/a + 1/b + 1/c = 1

a.b + b.c + c.a = a.b.c

BONS ET PARFAITS
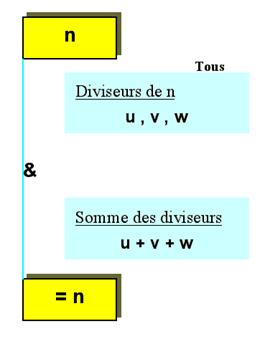
Nombres bons	Nombres parfaits
Exemples 11 = 2 + 3 + 6 1/2 + 1/3 + 1/6 = 1	6 est divisible par 1, 2 et 3 1 + 2 + 3 = 6

Voir Nombres parfaits

Suite	Exploration Sommes d'inverses proches de 1 ou de ½ Somme harmonique
Voir	Fractions – Glossaire Fractions – Multiplication Fractions égyptiennes Fractions continues Table des fractions égyptiennes Sommes des inverses des chiffres Nombres semi-parfaits primaires
DicoNombre	Nombre 1
Cette page	http://villemin.gerard.free.fr/Calcul/Fraction/Pde1a100/Fr1appro.htm