|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
MULTIPLICATIONS de
divers p Curieuses
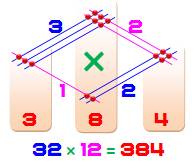
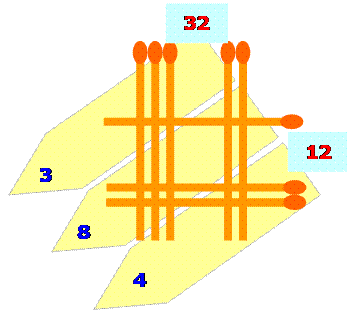
dispositions, mais efficaces. Celle présentée ci-contre est dite
par jalousies. On dispose les nombres à multiplier sur deux côtés: ici en
haut et à droite. Une autre présentation les met en haut et à gauche
(ci-dessous) |
|
|
|
||
|
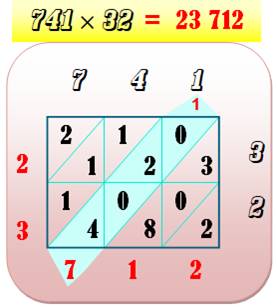
Exemple: 4 x 8 = 32; 4 x 7 = 28 …
Exemple: 8 + 1 + 9 = 8
|
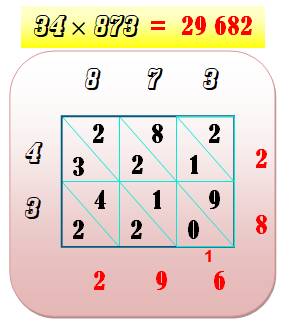
Exemple
Calculs
sur diagonale descendante. Notez que les
chiffres de la multiplication sont notés à la suite dans le sens horaire. On
reprend dans l'autre sens pour le résultat. |
|
|
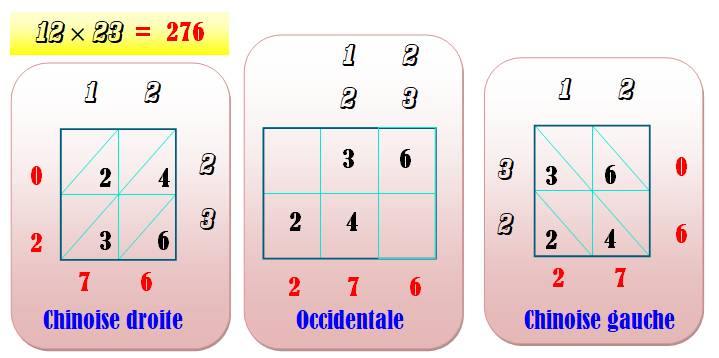
Les trois méthodes comparées
|
||
Anglais: lattice method
|
Divers
noms pour cette méthode ou d'autres proches
Usage
Vocabulaire
Historique
D'Inde, la
méthode se répandit vers la Chine, la Perse puis le reste du monde arabe. Ce
que nous avaons en terme de dates
|
|
|
||
|
|
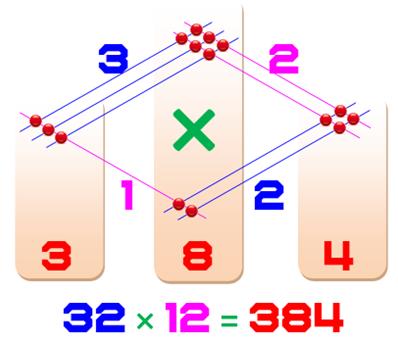
32 x 12
= 384 |
|
|
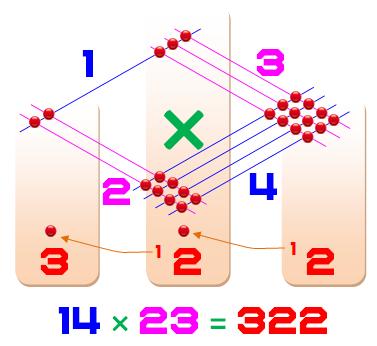
Autre
exemple (avec retenues) |
|
|
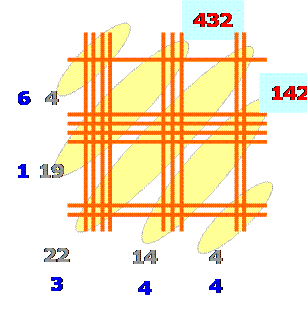
Avec 14, je pose 4 et garde 1; Avec 22, j'ajoute la retenue, ce qui
donne 23; je pose 3 et je garde 2 en retenue … |
432 x
142 = 61 344 |
Voir Méthode avec les doigts / Division à traits
Disposition
en oblique montrant directement les additions à effectuer (avec ou sans
retenue)
![]()
|
Méthode
utilisée par les
Égyptiens |
|
||
|
|
19 x 11 19
= |
16 + 2 + 1 |
|
|
Le 2e nombre est
multiplié par chacune des puissances de deux qui forment le 1er
nombre. |
1 2 4 8 16 |
11 22 0 0 176 |
|
|
|
|
209 |
|
Voir Binaire –
Multiplication
|
|
||
|
Variante plus élaborée de la méthode égyptienne. |
||
|
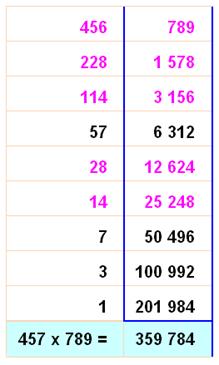
Méthode dite à la
russe utilisant les puissances de 2 Le
multiplicateur est décomposé en une
somme de puissances de 2. Sur l'exemple: 456 x 14 = 456 x (8 + 4 + 2) = 456 x 2
+ 456 x 4 + 456 x 8 |
|
|
|
Méthode de la
multiplication paysanne russe en multipliant et en divisant par 2 (sans
s'inquiéter des puissances de 2). |
||
|
Méthode On divise l'un par deux. On multiplie l'autre par deux. On ne
retient que les nombres à droite, en face d'un nombre impair à gauche. On ajoute
les nombres retenus. |
Exemple
1
|
Exemple
2
|
|
Variantes On
simplifie la présentation en ne conservant que deux colonnes et en barrant
les lignes paires (exemple à gauche) L'ordre
des facteurs est indifférent (exemple à
droite) |
Exemple
2 (bis)
|
Exemple
2 (ter)
|
|
Autre
exemple
|
Application
sur tableur
|
|
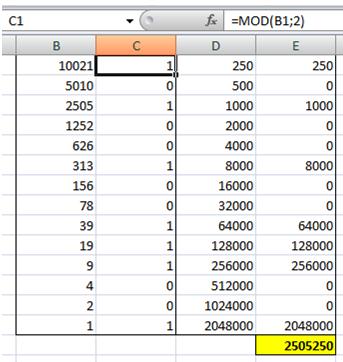
En colonne B, on calcule le PLANCHER de la
cellule supérieure divisée par 2. En colonne C, on calcule le MODULO 2 du
nombre à gauche. En colonne D, on prend le double de la
cellule supérieure. En colonne E, on fait le produit de C par D,
et en pied de colonne, on effectue la somme. Bilan: 10 021 x 250 = 2 505 250 |
|
Voir Autres applications avec tableur
|
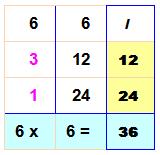
Explications
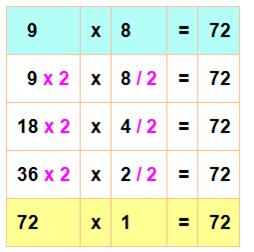
avec un cas simple Voyez la
multiplication de 9 par 8 dont le produit est 72. En multipliant
un des facteurs par 2 et en divisant l'autre par 2 on ne change pas le
résultat de la multiplication. On
reproduit ce procédé jusqu'à ne plus pouvoir diviser par 2. C'est le résultat
de la multiplication. Observez que 1, 2, 4
et 8 sont les puissances de 2 successives |
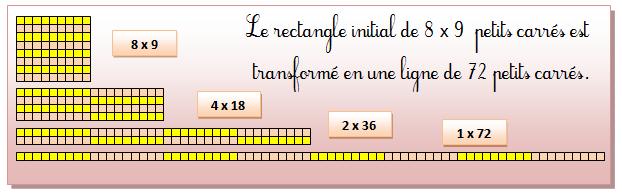
En divisant 8 par 2 jusqu'à la fin et en compensant en multipliant par
2 le nombre 9, on ne change pas le résultat de la multiplication. |
|
|
Illiustration
|
||
|
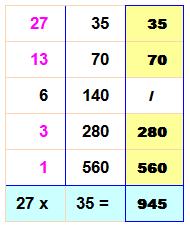
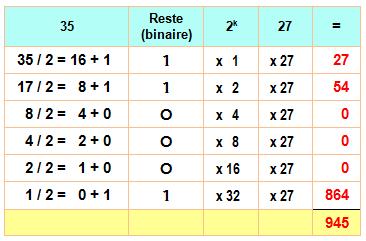
Explications
complètes On a
compris que la méthode est basée sur une sorte de représentation en
puissances de 2, ou binaire. Mieux qu'une
explication formelle fastidieuse, le tableau montre comment opèrent les
puissances de 2 successives selon que la représentation binaire comporte des
1 ou non. On retrouve la
division par 2 (colonne de gauche) et la multiplication par 2 (troisième colonne). |
Numération classique (exemple 35) 35 =
32 + 2 + 1 35 =
1 x 25 + 0
x 24 + 0 x 23 + 0 x 22 + 1
x 21 + 1 x 20 35
= 1000112 Méthode russe (division par 2) 35 /
2 = 16 reste 1 17 /
2 = 8 reste 1 4 / 2 =
2 reste 0 2 / 2
= 1 reste 0 1 / 2 =
0 reste 1 On
retrouve la représentation binaire de 35 (en remontant). La
multiplication 35 x 27 devient: (32
+ 2 + 1) x 27 Tableau explicatif
|
|
Voir Autre
méthode de multiplication sans table – (doublements et addition)
|
|
||||||||||
|
soit : a, b et c ces restes. Ne
connaissant que des trois restes, donnez
le nombre d'origine! |
Exemple 468
|
|||||||||
|
N = reste de ou plus mathématique N =
(715a + 364b + 924c) mod 1 001
715 = 5 x 11 x 13 = 102 x 7 + 1
|
Avec 6, 6 et 0, il s'agit de retrouver le nombre du départ Voici le calcul à effectuer
|
|||||||||
Voir Théorème des restes
chinois
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()