|
|||||||||||||||||||||||||||||||||||||||
![]()
|
Multiplication des FRACTIONS Principe et illustration amusante. |
|
|
||
|
Par un
entier k |
Approche:
Si nous sommes deux, moi et mon frère, à manger un
quart de tarte, nous en mangerons deux fois un quart, soit une demie tarte. Procédé:
Pour multiplier une fraction par un nombre entier,
on multiplie son numérateur par ce nombre. Puis, on procède à la
simplification de la fraction, s'il y lieu. Il est parfois, plus simple de
simplifier avant multiplication.
Exemples:
Vérification:
les fractions sont l'expression des nombres rationnels. En passant par leurs développements
décimaux, il est
possible de vérifier un calcul de fractions au moyen de la calculette. 15 x 3/12 =
45/12 15 x 0,25 =
3,75 |
|
|
Par une
fraction |
Approche:
Une tarte est partagée en quarts. Si je prends deux parts de tarte, cela fera
deux quarts (soit une demi-tarte). Par contre, si je n'en prends que la
moitié, cela ne fera que la moitié du quart soit un huitième. Autrement dit:
½ fois ¼ = 1/8. Autre cas: j'ai deux parts et je n'en prends que la moitié,
cela me fera une part. Ce que j'écris: 2/4 x 1/2 = 2/8 = 1/4. Procédé:
Pour multiplier deux fractions, on multiplie les
numérateurs et de même pour les dénominateurs. Il est pratique de d'abord
effectuer les simplifications qui se présentent avant d'effectuer les
multiplications.
Exemples:
Vérification:
le passage en décimal est recommandé pour vérifier
le calcul avec les fractions. 2/13 x 17/99 =
34/1287 0,1538… x
0,1717… = 0,0264 … Généralisation: Cette remarque montre qu'il est tout à fait possible de multiplier une
fraction par un nombre décimal. 2,5 x 1/4 = 2,5
/4 = 5/8 2,5 x 0,25 =
0,625 En notant que
2,5 c'est 5/2, le calcul aurait pu être: 5/2 x 1/4 = 5/8 |
|
|
|
|
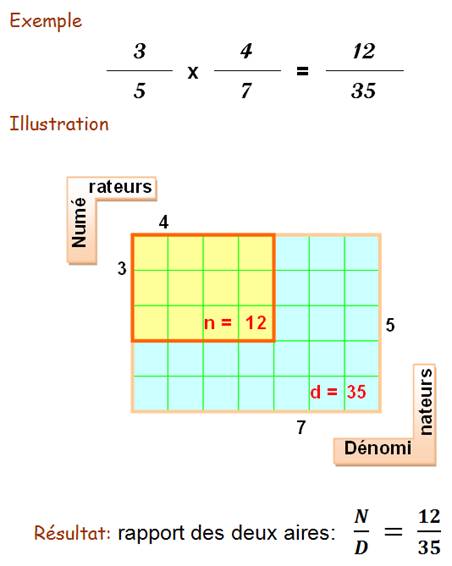
Voici une manière de
représenter une multiplication de deux fractions avec des surfaces dont le
rapport des aires donne le produit des fractions.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()