|
|||||||||||||||||||||||||||||||||||
![]()
|
Construction de la
médiatrice |
|
|
|
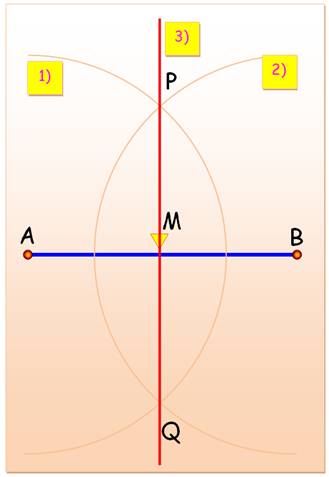
1) Cercle
de centre A de rayon quelconque (plus
grand que la longueur estimée de AM). 2) Avec la même ouverture du compas, cercle de
centre B. Ces deux cercles se coupent en P et Q. La droite
PQ est la médiatrice
du segment AB. 3) avec la règle joindre PQ qui coupe AB en M,
milieu de AB. |
|
|
|
|
|
|
1) Cercle de centre A de rayon AB. 2) Cercle de centre B de rayon AB. Les deux cercles se coupent en P et Q. Avec une
règle il suddirait comme ci-dessus de tracer le segment PQ. 3) Avec le même rayon AB, marquez les points R, S
T et U (cercle de rayon AB et de centre P qui coupent les cercles existants
en R et T, etc.)
4) Cercle de centre S de rayon SB. 5) Cercle de centre U de rayon UA. Ces cercles créent les points C et D. 6) Cercle de centre D de rayon DA. 7) Cercle de centre C de rayon CB. Ces cercles se coupent en M, milieu de AB. |
|
|
Voir Démonstration
en triangles isocèles |
![]()
|
Suite |
|
|
Voir |
|
![]()