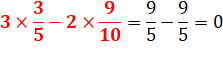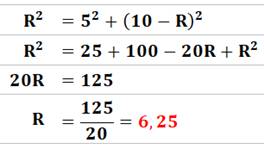|
||||||||||||||||||||||||||||||||
![]()
|
Une droite, c'est une chose qui se comprend
immédiatement. On embrouille l'esprit à
chercher à la définir davantage. Pascal (1623 - 1662) Plus court chemin d'un
cœur à un autre, sa ligne droite doit s'inscrire dans un triangle. Définition du string selon Philippe
Bouvard Dans divers arts, et
principalement dans l'art d'écrire, le meilleur chemin entre deux points même proches n'a jamais été, et ne sera
jamais, et n'est pas la ligne droite. José Saramago Par deux points fascistes, passe une extrême droite et une seule. Jean Yanne Est-ce que l’on peut
considérer que le zèbre est un animal de trait
? |
Voir Pensées & humour
|
DROITES
|
Voir Expression
avec le mot "droite"
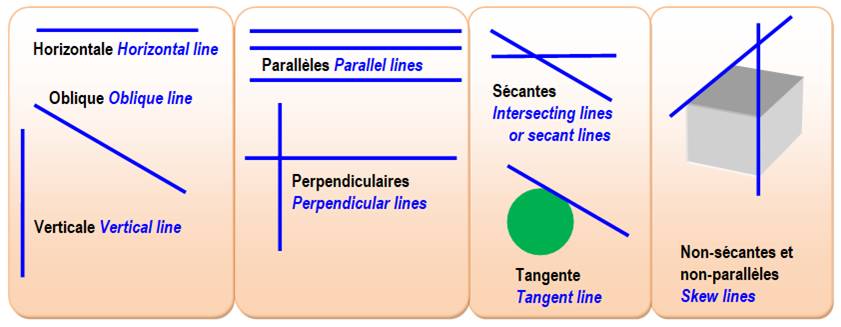
Types de droites
|
|
|
|
Suite en Postulat d'Euclide. |
|
|
|
||
|
Euclide IIIe siècle av.
J.-C. |
Autrement dit:
|
|
|
Archimède 287 - 212 av. J.-C. |
Autrement
dit:
|
|
|
Proclus 412 - 485 |
|
|
|
Roberval 1602 - 1675 Gauss 1777 - 1855 |
|
|
|
Larousse |
|
|
|
Mathématiques abstraites |
On pourr
|
|
|
Moderne |
|
|
D'après
Fourier
par Jean Dhombres et Jean-Bernard Robert
![]()
|
|
||
|
Point intermédiaire |
|
|
|
Continuité |
|
|
|
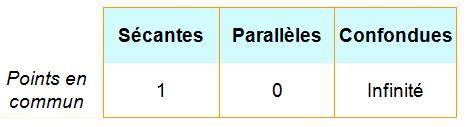
Sécante |
|
|
|
Chemin |
|
|
|
Alignement |
|
|
|
Éclipse |
|
|
|
Trois cas pour deux droites
dans un plan |
|
|
|
|
||
|
|
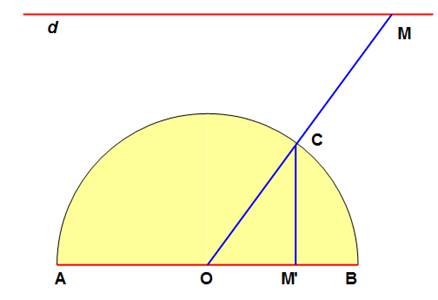
Il y a autant de points sur le segment AB que sur la droite d et
autant sur le demi-cercle ACB, d'ailleurs. On trace OM puis CM'. À tout point M de d correspond un
point C du demi-cercle. Et donc un point M' appartenant au
segment AB. |
|
Voir Infini et cercle / Infini et nombres réels
|
Par
deux points fascistes passe une extrême droite et une seule. Jean Yanne |
|
|
||
|
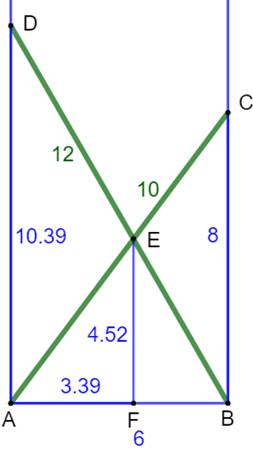
Deux
piliers et deux cordes tendues du sommet de l'un au pied de l'autre. Quelles
sont les coordonnées du point d'intersection? |
||
|
|
|
|
Anglais; two vertical poles or pillars / two strings are tied,
each of them from
the top of one pillar to the bottom of the other.
![]()
|
L'équation
de la droite est donnée en page sur les fonctions affines. Nous
intéressons ici à l'équation cartésienne
introduite en classe de première sous la forme d'un bref résumé des
définitions et le développement de quelques exercices. |
|
|
||||
|
|
Ax + By + C = 0
Vecteur directeur |
|||
|
|
Monde cartésien Ax + By + C = 0
|
Monde classique y = ax + b a est la pente = b est l'ordonnée à
l'origine = |
||
|
|
|
|||
|
|
|
|||
|
|
|
|||
Voir Équation classique de
la droite avec exemples / Milieu
de l'arc / Droites
parallèles
Application à la recherche
du rayon du cercle inscrit dans le quart de cercle
Les flèches des vecteurs sont omises
(pas de confusion possible, ici)
|
|
||
|
Question Que peut-on dire des trois
points I,J etK? Calculs IJ = IA + AJ IJ = – AI + AJ IJ = – 3/5 AB + 2AC IK = IA + AK IK = – AI + AK IK = – 3/5 AB + AK – 3AK + 3BK + 10CK = 0 – 3AK + 3(BA + AK) + 10(CA +
AK) = 0 – 3AK + 3BA + 3AK + 10CA + 10AK = 0 3BA + 10CA + 10AK
= 0 – 3AB – 10AC + 10AK = 0 – 3AB – 10AC = – 10AK 3AB + 10AC = 10AK 3/10 AB + AC = AK IK = – 3/5 AB + 3/10AB + AC IK = – 6/10 AB + AC IK = – 3/10AB + AC 2IK = – 3/5 AB + 2AC IJ = 2
IK |
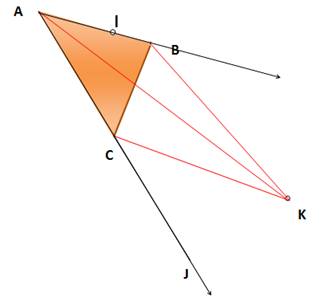
Données Triangle ABC Point I au 3/5 de AB Point J au double de AC Point K tel que: – 3AK + 3BK + 10CK = 0 Figure
Conclusion IKJ sont alignés et K est au
milieu de IJ. La figure est fausse. Pas de
souci. Elle nous a permis d'y voir plus clair. |
|
|
Exercice 2 |
|
|
|
Question MA + 2BM – 5MC = BC Exprimer AM. Calculs – AM + 2(BA + AM) – 5(MA + AC) = BA + AC – AM – 2AB + 2AM + 5AM – 5AC = – AB + AC 6AM – 2AB – 5AC = – AB + AC 6AM = 2AB + 5AC – AB + AC 6AM = AB + 6AC AM = 1/6AB + AC |
sans figure |
|
|
Exercice 3 |
|
|
|
Données Parallélogramme ABCD Point E au triple de AB Point F à 3/2 de AD
Question Que dire des points E, F et
C? |
||
|
Calculs EC = EA + AC EC = – AE + AC EC = – 3AB + AC EC = – 3AB + AD + DC EC = – 3AB + AD + AB EC = – 2AB + AD |
CF = CA + AF CF = – AC + 3/2 AD CF = – (AD + DC) + 3/2 AD CF = – AD – DC + 3/2 AD CF = – 2/2AD – DC + 3/2 AD CF = 1/2AD – AB 2CF = AD – 2AB ECF sont alignés |
|
|
Exercice 4 |
|
|
|
Question 2x – 3y + 4 = 0
Montrez que la droite définie par cette équation
et le vecteur w sont colinéaires. |
Solution
En rouge, cette sorte de produit en croix est
appelée déterminant des deux vecteurs. Le déterminant est nul, les vecteurs u et w sont
colinéaires. |
|
|
|
||
|
Question Un couloir de 6 m de large, bordé par deux murs
verticaux Deux échelles sont posées contre chacun des murs.
Leur pied s'appuyant sur le mur opposé. Quelles sont les coordonnées du point de
croisement E ? Réponse Mise équation des deux droites portant les
échelles et calcul de x pour une valeur commune de y (intersection des
droites):
|
Illustration Couloir en bleu
et
|
|
|
Construction Une
équerre de 10 par 5. Un
cercle centré sur le grand bras de l'équerre passe par ses deux extrémités. Quel
est le rayon du cercle ? Piste Pythagore
appliqué au triangle rectangle. Calculs
|
|
|
|
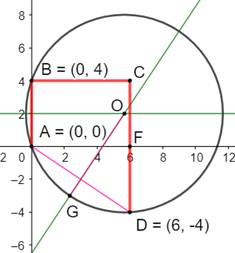
Construction Une
sorte de U formé de trois segments perpendiculaires de longueurs 4, 6, 8. Quel
est le rayon du cercle passant trois de ses points ? Méthode analytique Le
centre du cercle est situé sur les médiatrices
des cordes AB et AD. Il s'agit en fait de trouver le rayon
d'un cercle passant par trois points connus.
Ici: A, B et D. Le
calcul analytique semble bien adapté. Le centre du cercle est commun aux deux
médiatrices (droites vertes) dont on va calculer les
équations. Le
rayon, égal à la distance OA, sera calculé avec le théorème
de Pythagore Calculs
|
Défi: calculer le rayon
Notations
|
|
|
Méthode géométrique On
s'intéresse aux deux triangles bleus. Avec le théorème de Pythagore, on
calcule h et g sachant que h + g = 6.
|
|
|
Voir Défis en
géométrie / Trois
méthodes pour trouver l'équation d'un cercle passant par trois points
![]()
|
Suite |
|
|
Incontournables |
|
|
Voir |
|
|
Dicomot |
|
|
Cette page |
![]()