|
|||||||||||||||||||||||||||||||||||
![]()
|
Construction d'un carré dans un triangle CONSTRUCTIONS
ASTUCIEUSES. Problème qui semble
complexe tant que l'on ne connaît pas l'astuce. |
|
|
||
|
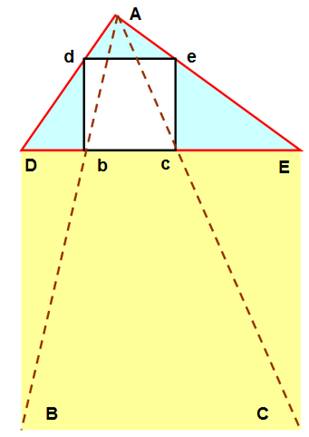
Question Inscrire un carré dans un triangle quelconque. Un de ses côtés est sur un des côtés du
triangle (base). Deux sommets sont de part et d'autre de la
pointe opposée à la base du triangle. |
|
|
|
|
||||||||||||||||||
|
Réponse Dessinez le carré de côté égal à la base du
triangle (jaune). Tracez AB et AC joignant le sommet du
triangle aux deux sommets à la base du carré (pointillés). Ces segments coupent la base du triangle en
b et c, déterminant les sommets de base du carré recherché. Deux perpendiculaires en b et c coupent les
côtés du triangle en d et e les deux autres côtés du carré. |
|
|||||||||||||||||
|
Explications
|
||||||||||||||||||
![]()
|
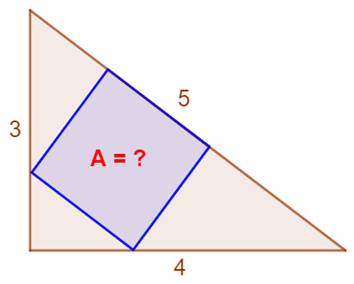
Construction Un
triangle dont les côtés mesurent 3, 4 et 5 unités. Un
carré est inscrit sur l'hypoténuse. Quelle
est l'aire de ce carré ? Piste Le
triangle
3, 4, 5 et un triangle rectangle. Du fait des parallèles, les trois triangles
marron sont semblables
au triangle initial. Soit
a, b et c les coefficients d'homothétie
(de proportionnalité). La
figure du bas traduit ces informations. Calculs
|
|
|
Voir Défis
géométriques – Index
|
Construction Un
triangle dont les côtés mesurent 3, 4 et 5 unités. Un
carré est inscrit sur les côtés de l'angle droit. Puis,
un cercle est inscrit dans un des triangles formés. Calculer
le côté du carré et le rayon du cercle. Application
numérique avec a = 3 et b = 4. Piste On
sait inscrire un
carré dans le triangle rectangle. On
sait inscrire le
cercle dans le triangle rectangle. Le
théorème
de Pythagore permettra de calculer les dimensions du triangle DAE. Calculs |
Figure avec notations
Figure avec application numérique
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()