|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUZZLES ARITHMÉTIQUES Cryptarithmes ou
cryptogrammes Addition de pastilles de couleur Une pastille de
couleur correspond toujours au même chiffre. Reconstituer l'opération complète. |
|
|
||
|
Problème
Notations
|
|
|
Source: télé 7 jeux n°60 – 2014
Codage de
la grille d'addition

|
|
|||
|
|
4B + r2 |
= 10r3 + B |
|
|
|
|
||
|
|
|
||
|
|
|||
|
|
2R + 4 2R |
= J < 10 = J – 4 |
|
|
|
R ou |
= (8 – 4 ) / 2
= 2 = (6 – 4 ) / 2
= 1 |
|
|
|
J R |
= {8, 6} = {2, 1} |
|
|
|
2J + 6 |
= 10r1 + R |
|
|
|
2 x 8 + 6 |
= 22 compatible avec R = 2 |
|
|
|
2 x 6 + 6 |
=18 incompatible avec R = 1 |
|
|
|
|
||
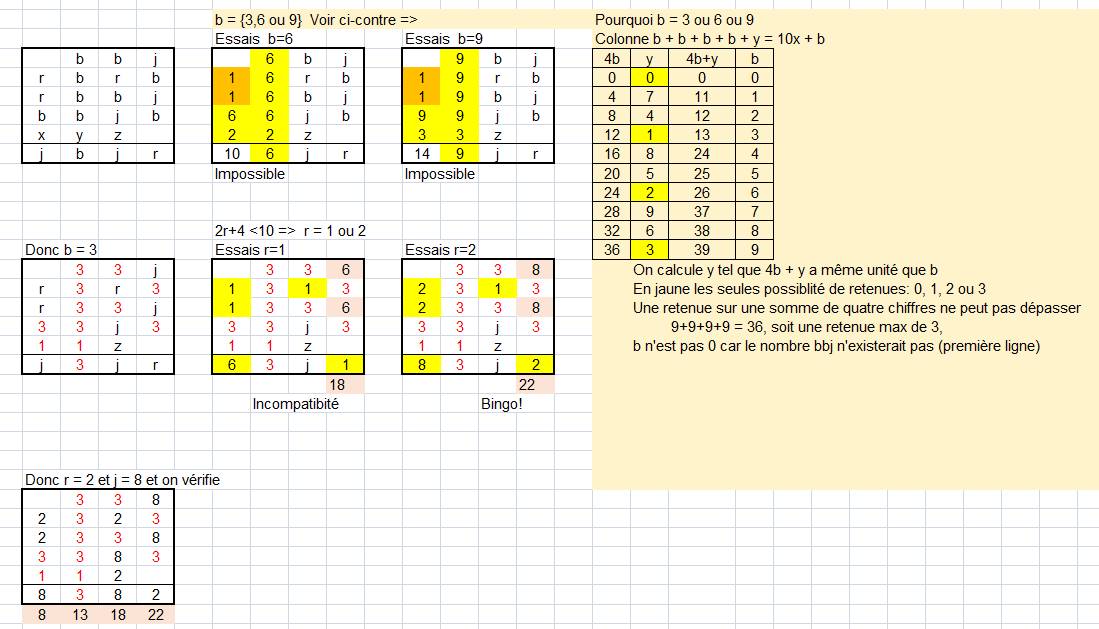
Pour
explications complémentaire: résolution avec tableur
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Livre |
Passionnant! |
|
Cette page |
![]()




