|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUZZLES
ARITHMÉTIQUES Cryptarithmes – Cryptogrammes Arithmétique verbale HOMME + FEMME = PARITE AMOUR + HAINE = NÉANT Deux exemples
de cryptarithmes ayant un sens manifeste, mais à solutions multiples. Exemple
de programmation pour résoudre de tels
puzzles arithmétiques. |
|
Présentation Ce puzzle
arithmétique (cryptarithme) publié par La
Recherche et Tangente en début
2020 est superbe par son message, et par le fait qu'il comporte les 10
chiffres représentés ici chacun par une lettre. Sa résolution
n'est pas très difficile. Elle se prête à
une résolution informatique pas trop gourmande en temps d'exploration de tous
les cas possibles. En bref un excellent exercice de codage. |
Énigme
Dix lettres utilisées {A, E, F, H, I, M, O, P, R, T} |
||||||||||||||||||||||
|
Observations Pour les unités,
seule possibilité: 0 + 0 = 0. Aucun autre chiffre doublé ne redonne la même
unité. E = 0. Deux additions
successives de M avec M. Les unités ne diffèrent que d'une unité. L'addition O + 0
n'engendre pas de retenue. La retenue produite par H + F est égale à 1 et P =
1. On note que H et
F sont interchangeables sans modifier la somme. Seules quatre lettres
restent inconnues dans l'adition. Celles de la somme en découlent. Il faut
simplement vérifier qu'elles sont différentes de celles déjà utilisées. |
Première observations
Quatre lettres à explorer {F, H, M, O} |
||||||||||||||||||||||
|
Une
des solutions |
|
||||||||||||||||||||||
Une
des énigmes créées par Élisabeth Busser, Gilles Cohen, Michel Criton,
Jean-Louis Legrand et Bernard Myers
|
|
Commentaire Réinitialisation Lettre E comme
valant 0. Exploration des
lettres M, H, O et F pour les valeurs de 1 à 9. (La
lettre O est doublée car elle est réservée dans ce langage). On vérifie que
ces valeurs sont distinctes: il faut que la liste comporte autant d'éléments
que l'ensemble.
Formation des
nombres de l'addition A + B et de la somme S. Avec la
conversion (convert) en base 10, on obtient
la liste des chiffres du nombre S. Avec l'ensemble
C, on réunit les chiffres des trois nombres A, B et C, sans oublier le 0. Si cet ensemble (de chiffres non répétés) contient dix
éléments alors nous tenons une solution.
On imprime les
solutions trouvées. Résultat Le programme propose
huit solutions. Comme nous l'avions
remarqué, il s'agit de deux jeux de quatre, avec échange des lettres H et F. Les auteurs de
l'énigme observent que R n'est PAIR que pour la première solution et sa
cousine en quatrième position. Ce qui constitue le seul cas où le nombre
"PAIR" est pair. |
|||
|
|
|
|
Deux exemples de solutions avec opération posée
Les 14 (x2) solutions ordonnées par sommes croissantes dont
11 avec U = 0 et 3 avec U = 9 doublées
(soit 28) en permutant O et I
|
|
|
|
|||
|
Vérification de la pertinence du puzzle |
|
||
|
Recensement des lettres |
A M
O U R
H I N
E T = 10 lettres
distinctes pour les 10 chiffres. 3 + 1 + 1 + 1 + 1 + 1
+ 1 + 3 + 2 + 1 = 15 lettres au total. |
||
|
Tentative de résolution raisonnée
|
Les
nombres de commencent jamais par un 0: A et H ne sont pas 0. A
et H au minimum valent 1 et 2; leur somme A+H = N est supérieure ou égale à
3: N différent de
0, 1, 2. |
||
|
|
Le
N est doublé sur l'avant-dernière colonne. La
valeur de U doit être neutre. U
vaut 0 ou 9 (s'il y a retenue sur la première addition). |
||
|
Si U = 0
|
Alors,
R et E ne sont pas nuls et valent au minimum 1 et 2: T ³ 3. La
somme R + E ne produit pas de retenue, si l'un vaut 1 l'autre vaut 8 au
maximum: R et N jamais 9 |
||
|
Etc. |
Pas
simple! |
||
|
|
||
|
Ce cryptarithme
utilise les dix chiffres.
Le programme examine toutes les permutations
des dix chiffres et ne retient que
celles qui donnent l'égalité recherchée. |
||
|
|
Initialisation. Utilisation du
package combinatoire. Mise à zéro d'un
compteur (kt) de solutions. Liste des
chiffres en L. Liste des
permutations de ces chiffres en LL et de leur quantité en qLL Lancement de qLL
boucles Identification
de chaque permutation en M. Calcul
numériques des mots: amour, haine et néant en respectant les répétitions de
lettres. Si l'opération
est juste, imprimez cette opération et ajouter un au compteur de solutions. Finalement
imprimiez la valeur du compteur. |
|
|
|
Impression des 28 solutions (durée
d'exécution: de l'ordre de la minute) |
|
Voir Programmation
![]()
Archives
Recherche
avec programmation moins élaborée, mais plus fastidieux.
|
|
||||
|
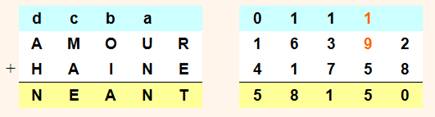
Mise en équation Avec exemple
numérique pour aider à la compréhension. La ligne ajoutée en haut sert à
matérialiser les retenues. |
|
|||
|
Calcul de la première
colonne. Pour faciliter le calcul avec les
retenues, nous allons distinguer la valeur de T, d'une part, et la somme de R et E, d'autre part. La fonction tronque donne la partie
entière d'un nombre, en supprimant toute la partie décimale |
SommeRE
= R + E |
2 + 8 = 10 |
||
|
a = la dizaine de
SommeRE. T= les unités de
SommeRE. |
a
= tronque(SommeRE / 10) T
= SommeRE – 10*a |
a = tr (10/10) = 1 T = 10 – 10x1 = 0 |
||
|
Procédons de la
même manière pour la colonne suivante. |
SommeUN
= a + U + N |
1 + 9 + 5 = 15 |
||
|
b = la dizaine de
SommeUN . Inutile de
calculer N. |
b
= tronque(SommeUN / 10) |
b = tr (15/10) = 1 |
||
|
Colonne 3. |
SommeOI
= b + O + I c
= tronque(SommeOI / 10) A
= SommeOI – 10*c |
1 + 3 + 7 = 11 c = tr (11/10) = 1 A = 11 – 10x1 = 1 |
||
|
Colonne 4. |
SommeMA
= c + M + A d
= tronque(SommeMA / 10) |
1 + 6 + 1 = 8 d= tr (8/10) = 0 |
||
|
Colonne 5: seul H
est inconnue. |
H
= N – A - d |
5 – 1 – 0 = 4 |
||
|
Principe de l'algorithme Analyse
systématique des valeurs des lettres. Les autres se déduisent par calcul. |
R, E,
U, N, O, I, M T, A, H |
|
Filtrage des valeurs
des lettres pour ne conserver que les cas où elles sont différentes. Il faut noter que le test sur la
somme et le produit des 10 chiffres est une condition nécessaire mais pas
suffisante. Il faudra soigneusement vérifier les
résultats pour éliminer les artefacts: ce programme va sortir 33 réponses
pour 28 valides. |
0 + 1 + 2 + 3 + 4 +
5 + 6 + 7+ 8 + 9 = 45 Produit 1 x 2x 3 x 4 x 5 x
6 x 7 x 8 x 9 x 10 = 10! = 3 628 800 (notez qu'il s'agit
du produit des chiffres plus 1 de manière à s'affranchir de la valeur 0) |
|
Les noms des lettres sont doublés
pour qu'elles ne soient pas confondues avec des noms réservés par le langage
(comme I pour le i imaginaire). |
> #AMOUR + HAINE = NEANT kt:=0: for RR from 0 to 9 do for EE from 0 to 9 do for UU from 0 to 9 do for NN from 0 to 9 do for OO from 0 to 9 do for II from 0 to 9 do for MM from 0 to 9 do SommeRE:=RR+EE:
aa:=trunc(SommeRE/10):
TT:= SommeRE-10*aa: SommeUN:=UU+NN+aa:
bb:=trunc(SommeUN/10): SommeOI:=OO+II+bb: cc:=trunc(SommeOI/10): AA:=SommeOI-10*cc: SommeMA:=MM+AA+cc: dd:=trunc(SommeMA/10): HH:=NN-AA-dd: if (AA+MM+OO+UU+RR+HH+II+EE+NN+TT) and ((AA+1)*(MM+1)*(OO+1)*(RR+1)*(HH+1) then HAINE:=10000*HH+1000*AA+100*II+10*NN+EE: AMOUR:=10000*AA+1000*MM+100*OO+10*UU+RR: NEANT:=10000*NN+1000*EE+100*AA+10*NN+TT: if AMOUR+HAINE=NEANT then kt:=kt+1; lprint(Solution,kt): lprint(AMOUR): lprint(HAINE): lprint(NEANT): fi: fi: od:od:od:od:od:od:od: |
![]()
|
Suite |
|
|
Voir |
|
|
Livres et Sites |
|
|
Cette page |
![]()