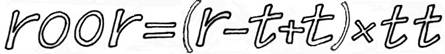|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUZZLES ARITHMÉTIQUES Cryptarithmes ou
Arithmétique verbale Aussi: alphamétique ou
cryptarithmétique Arithmétique cryptée Cryptogrammes Alphametic Casse-tête, cryptogramme, pour lequel une lettre
correspond à un chiffre. On donne l'opération en lettres, il faut trouver
celle en chiffres. Lorsque les lettres
ont une signification J. Hunter a introduit le terme: alphametic. Quatre beautés
(mais pas toujours au rendez-vous):
|
Anglais: Verbal arithmetic, alphametics, cryptarithmetic,
cryptarithm or word addition
|
Pour un cryptarithme avec résolution
expliquée en détail voir |
|
|
Voir Solution
|
Définition Cryptarithme
dans lequel les éléments forment des mots qui ont une signification. Une
opération en mots ayant un sens est proposée; il faut trouver les chiffres
associés à chaque lettre pour obtenir une opération exacte. Historique SEND +
MORE = MONEY => 9567 + 1085 = 10 652 Le premier
alphamétique connu, proposé par Ernest Dudeney (1857-1930). Le nom a
été donné en 1955 par James Aiston Hope Hunter (canadien). Exemples CINQ × SIX
= TRENTE => 5409 × 142 = 768 078 FRAISE +
CITRON + CERISE = RAISIN => 297 610
+ 368 945 + 309 610 = 976 165 PAPA +
PAPA = MAMAN => 7 575 + 7 575 = 15
150* (Voir résolution ci-dessous) Cas
AB + CD = EF |
* Créé par Matthieu
Dufour

Voir Brève
875
|
|
|||||||||||||||||||||||||||||||||
|
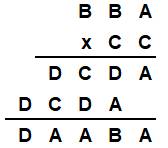
Cette
addition ne comporte que trois chiffres différents, chacun est représenté par
une lettre. Rétablir
la solution unique. |
|
||||||||||||||||||||||||||||||||
|
Avec si
peu d'inconnues, les équations semblent un bon moyen. L'addition
est donc posée sans oublier de tenir compte des retenues. Idée:
garder les retenues comme seules inconnues, car elles ne prennent que peu de
valeurs (0, 1 ou 2). |
|
||||||||||||||||||||||||||||||||
|
Aux
extrêmes, les équations sont simples. |
2A + 2B = 10r + B => B = 10r
– 2A 2C + t = B => C = (B – t) /2 |
||||||||||||||||||||||||||||||||
|
En utilisant
la représentation décimale des nombres, la somme complète s'écrit: |
32A + 302B + 2010C = 100A +
1001B + 10C 68A + 699B = 2000C |
||||||||||||||||||||||||||||||||
|
En
remplaçant B et C: |
68A + 699(10r – 2A) = 1000(10r
– 2A – t) 670A = 3010r – 1000t
|
||||||||||||||||||||||||||||||||
|
Or r et t
valent (0, 1, 2) Calcul ou
tableur => |
Valeur entière de A (= 6)
seulement pour r = t = 2 |
||||||||||||||||||||||||||||||||
|
Calcul de
B et C: |
B = 10r – 2A = 20 – 12 = 8 C = (B – t)/2 = (8 – 2)/2 = 6 |
||||||||||||||||||||||||||||||||
|
Seule
solution => Une exploration par programmation
confirme cette unicité. |
|
||||||||||||||||||||||||||||||||
Merci à Claude Renouf pour l'idée de cette
énigme
|
|
|||||||||||||||||||
|
Résoudre cette opération où chaque couleur
représente un chiffre. Solution Unités: Dizaines: 3d + 1 = …5 =>
d = 8 avec 2 de retenue. Centaines: 3c + 2 = 5 =
> c = 1. Bilan: 3 x 185
= 555. Il existe sept nombres à
trois chiffres dont le triple est un repdigit:
111x3 = 333; 148x3 = 444; 185x3 = 555; 222x3 = 666; 259x3 = 777; 296x3 = 888
et 333x3 = 999. Seul 185 reproduit ses unités (555). Notez que: 37 x 3 =
111 et 74 x 3 = 222. |
|
||||||||||||||||||
|
Chaque lettre doit être remplacée par un chiffre
|
Après deux
essais, la solution est trouvée
|
||||||||||||||||||
Exemple avec les quatre plus petits nombres premiers
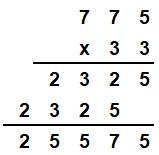
Cité par Martin Gardner
en 1962, sans doute plus ancien.
Voir Nombre 25 575
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Soleil,
sable et bikini
Voir Résolution de ce problème Four, way et stop
Clou, ocue et zero
Stir, two et wheat
Cette solution ne respecta
pas la règle: R et E devraient être différents. Mais … Ce cryptarithme est faible. En effet,
il y a bien dix lettres différentes pour dix chiffres, mais: aucune solution
sans chiffre doublé et chiffre manquant. Alors, il existe des
dizaines de solutions (plus de 80), comme les six suivantes:
Merci à M Barcanan pour ses remarques
Cats hate dogs
Cette énigme a 288 solutions. Celle présentée
est la plus petite pour CATS. Pour toutes, E vaut évidemment 0. Conclusion,
toute solution comportera tous les chiffres de 0 à 9, sauf un. Quelques solutions
avec mise en évidence des chiffres utilisés
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Résolution
pas à pas
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Résolution par programmation
/ Autre cryptarithme résolu par programmation
|
|
||||||||||||||||||||
|
ROLLS +
ROYCE = AUTOS pour AUTOS minimum |
|
|||||||||||||||||||
|
Solution
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
Voir nombre 34 879
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Explications
Dans sa plus simple
expression et dans sa forme générique
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Nombre
198
|
|
|
Si vous lisez à
l'envers vous trouverez l'égalité 77 x ( 7 + 7 – 1 )
= 1001 Génial, non! D'après Jean-Louis Alexandre |
Voir Chiffres
romains pour une autre du même type
![]()
|
Suite |
|
|
Voir |
|
|
Passionnant! |
|
|
Sites |
|
|
Cette page |
![]()