Tables des facteurs des nombres

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/11/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TABLES
Débutants Nombres	FACTEURS			Glossaire Nombres
INDEX Table	Facteurs 1 à 299	Facteurs 300 à 1010	Puissances
	Nature 1 à 999	Diviseurs en puissances	Quantité de facteurs identiques
	Sommaire >>> Nombres voisins avec même quantité de facteurs >>> Nombres composés sandwiches autour d'un premier >>> Nombres consécutifs avec même quantité de facteurs (tous) >>> TABLE des facteurs des nombres de 1 à 299

Facteurs et diviseurs

des nombres de 1 à 299

Facteurs

Diviseurs

Quantité de diviseurs

Somme des Diviseurs propres

Rappel: les nombres premiers sont ceux qui ont

un seul facteur (lui-même), soit
deux diviseurs seulement (1 et lui-même).

La somme des diviseurs propres est égale à 1.

Facteurs et diviseurs

Glossaire

Explications

Théorie

Fonctions arithmétiques

Quantité de facteurs uniques et répétés

Types de nombres selon leurs facteurs

Pour consulter le détail sur chaque nombre

Dictionnaire des nombres

Nombres voisins avec même quantité de facteurs

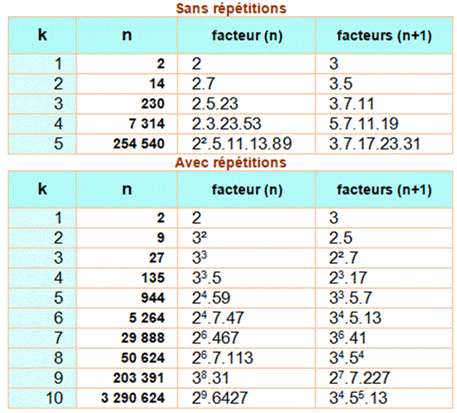
Exemples

Les nombres 230 et 231 ont tous deux 3 facteurs, et ce sont les plus petits nombres ayant cette propriété.

Les nombres 135 et 136 ont tous deux 4 facteurs, y compris les facteurs répétés, et ce sont les plus petits de ce genre.

Nombres composés sandwiches autour d'un premier

On s'intéresse au nombre composé (p – 1) et (p + 1) autour des nombres premiers p. On compte la quantité de facteurs de ces deux nombres et on retient le plus petit ayant k facteurs:

Exemple pour k = 3: 130 = 2.5.13 / 131 premier / 132 = 2².3.11

Pour les k successifs on a:

Nombre premier 1-sandwich: 3

Nombre premier 2-sandwich: 11

Nombre premier 3-sandwich: 131

Liste pour le nombre central premier

3, 11, 131, 1429, 77141, 3847271, 117048931, 22917541219, 1771365487891, 140734085123059, 14159733947566481, …

Liste pour le nombre central quelconque (premier ou composé)

3, 11, 131, 1429, 77141, 1456729, 117048931, 10326137821, 1110819807371, 140734085123059, 11639258217451019, …

Anglais: Smallest prime sandwiched between two numbers having exactly k prime divisors

Voir Nombres sandwiches

Nombres consécutifs avec même quantité de facteurs (tous)

Avec 9 et 10: deux nombres consécutifs avec deux facteurs.

Avec 602 à 606: cinq nombres consécutifs avec trois facteurs.

Et ce sont les cas avec les nombres les plus petits

2 (2)

3 (2)

4 et 5 (3)

6 (3)

9 = 3 × 3

10 = 2 × 5

33 = 3 × 11

34 = 2 × 17

35 = 5 × 7

602 = 2 × 7 × 43

603 = 3 × 3 × 67

604 = 2 × 2 × 151

605 = 5 × 11 × 11

606 = 2 × 3 × 101

2 522 = 2 × 13 × 97

2 523 = 3 × 29²

2 524 = 2² × 631

2 525 = 5² × 101

2 526 = 2 × 3 × 421

2 527 = 7 × 19²

2 528 = 2⁵ × 79

2 529 = 3² × 281

7 (3)

8 et 9 (4)

211 673 = 7 × 11 × 2 749

211 674 = 2 × 3 × 35 279

211 675 = 5² × 8 467

211 676 = 2² × 52 919

211 677 = 3 × 37 × 1 907

211 678 = 2 × 109 × 971

211 679 = 13 × 19 × 857

3 405 122 = 2 × 7 × 29 × 8 387

3 405 123 = 3² × 19 × 19 913

3 405 124 = 2² × 127 × 6 703

3 405 125 = 5³ × 27 241

3 405 126 = 2 × 3 × 59 × 9 619

3 405 127 = 11 × 23 × 43 × 313

3 405 128 = 2³ × 425 641

3 405 129 = 3 × 7 × 13 × 12 473

3 405 130 = 2 × 5 × 167 × 2 039

Voir Suite de nombres consécutifs avec même quantité de facteurs distincts

Nombres consécutifs avec même unité du plus grand facteur

Impossible, évidemment, avec 5 et les unités paires.

Voir Nombre 12 / Nombre 52 / Nombre 121 / Nombre 187 / Nombre 583

Nombres consécutifs avec les mêmes chiffres dans leurs facteurs

Exemples

Les facteurs des nombres 8 et 9 sont formés avec les chiffres {2 et 3}.

Les nombres 146, 147 et 148 sont le plus petit triplet de nombres consécutifs a avoir les mêmes chiffres pour facteurs {1, 2, 3, 7}.

Ils sont quatorze tels nombres jusqu'à 1000.

Cas de trois nombres consécutifs avec mêmes chiffres dans leurs facteurs

Voir Nombre 146 / Nombre 8 762

TABLES

Facteurs

Diviseurs

Quantité

Somme'

Note

(1)

(2)

(3)

(2)^2

(5)

(2)*(3)

(7)

(2)^3

(3)^2

{1}

{1, 2}

{1, 3}

{1, 2, 4}

{1, 5}

{1, 2, 3, 6}

{1, 7}

{1, 2, 4, 8}

{1, 3, 9}

Ni premier, ni composé

Premier

Composé, déficient

Premier

Composé, parfait

Premier

Composé, déficient

Rappel: le chapeau exprime la puissance 2^2 = 2²; l'astérisque * indique la multiplication

La somme donnée est celle des diviseurs propres (somme', marquée avec un prime)
Elle permet d'apprécier l'abondance ou la déficience d'un seul coup d'œil.

Quantité record de facteurs

Facteurs multiples (y compris les facteurs répétés)

Tous: [1, 2], [2, 4], [3, 8], [4, 16], [5, 32], [6, 64], [7, 128], … = 2^k

Hors puissances de 2 pures: [1, 3], [2, 6], [3, 12], [4, 24], [5, 48], [6, 96], [7, 192], [8, 384], [9, 768] ,[10,1536],[11,3072],[12,6144], … = 2 x 3^k

Hors nombres pairs: [1, 3], [2, 9], [3, 27], [4, 81], [5, 243], [6, 729], [7, 2187], [8, 6561] … = 3^k

Facteurs simples: [1, 2], [2, 6], [3, 30], [4, 210], [5, 2310], [6, 30030] … = primorielles. Exemple: 30 030 = 2x3x5x7x11x13

Facteurs

Diviseurs

Quantité

Somme'

(2)*(5)

(11)

(2)^2*(3)

(13)

(2)*(7)

(3)*(5)

(2)^4

(17)

(2)*(3)^2

(19)

(2)^2*(5)

(3)*(7)

(2)*(11)

(23)

(2)^3*(3)

(5)^2

(2)*(13)

(3)^3

(2)^2*(7)

(29)

(2)*(3)*(5)

(31)

(2)^5

(3)*(11)

(2)*(17)

(5)*(7)

(2)^2*(3)^2

(37)

(2)*(19)

(3)*(13)

(2)^3*(5)

(41)

(2)*(3)*(7)

(43)

(2)^2*(11)

(3)^2*(5)

(2)*(23)

(47)

(2)^4*(3)

(7)^2

(2)*(5)^2

(3)*(17)

(2)^2*(13)

(53)

(2)*(3)^3

(5)*(11)

(2)^3*(7)

(3)*(19)

(2)*(29)

(59)

(2)^2*(3)*(5)

(61)

(2)*(31)

(3)^2*(7)

(2)^6

(5)*(13)

(2)*(3)*(11)

(67)

(2)^2*(17)

(3)*(23)

(2)*(5)*(7)

(71)

(2)^3*(3)^2

(73)

(2)*(37)

(3)*(5)^2

(2)^2*(19)

(7)*(11)

(2)*(3)*(13)

(79)

(2)^4*(5)

(3)^4

(2)*(41)

(83)

(2)^2*(3)*(7)

(5)*(17)

(2)*(43)

(3)*(29)

(2)^3*(11)

(89)

(2)*(3)^2*(5)

(7)*(13)

(2)^2*(23)

(3)*(31)

(2)*(47)

(5)*(19)

(2)^5*(3)

(97)

(2)*(7)^2

(3)^2*(11)

{1,2,5,10}

{1,11}

{1,2,3,4,6,12}

{1,13}

{1,2,7,14}

{1,3,5,15}

{1,2,4,8,16}

{1,17}

{1,2,3,6,9,18}

{1,19}

{1,2,4,5,10,20}

{1,3,7,21}

{1,2,11,22}

{1,23}

{1,2,3,4,6,8,12,24}

{1,5,25}

{1,2,13,26}

{1,3,9,27}

{1,2,4,7,14,28}

{1,29}

{1,2,3,5,6,10,15,30}

{1,31}

{1,2,4,8,16,32}

{1,3,11,33}

{1,2,17,34}

{1,5,7,35}

{1,2,3,4,6,9,12,18,36}

{1,37}

{1,2,19,38}

{1,3,13,39}

{1,2,4,5,8,10,20,40}

{1,41}

{1,2,3,6,7,14,21,42}

{1,43}

{1,2,4,11,22,44}

{1,3,5,9,15,45}

{1,2,23,46}

{1,47}

{1,2,3,4,6,8,12,16,24,48}

{1,7,49}

{1,2,5,10,25,50}

{1,3,17,51}

{1,2,4,13,26,52}

{1,53}

{1,2,3,6,9,18,27,54}

{1,5,11,55}

{1,2,4,7,8,14,28,56}

{1,3,19,57}

{1,2,29,58}

{1,59}

{1,2,3,4,5,6,10,12,15,20,30,60}

{1,61}

{1,2,31,62}

{1,3,7,9,21,63}

{1,2,4,8,16,32,64}

{1,5,13,65}

{1,2,3,6,11,22,33,66}

{1,67}

{1,2,4,17,34,68}

{1,3,23,69}

{1,2,5,7,10,14,35,70}

{1,71}

{1,2,3,4,6,8,9,12,18,24,36,72}

{1,73}

{1,2,37,74}

{1,3,5,15,25,75}

{1,2,4,19,38,76}

{1,7,11,77}

{1,2,3,6,13,26,39,78}

{1,79}

{1,2,4,5,8,10,16,20,40,80}

{1,3,9,27,81}

{1,2,41,82}

{1,83}

{1,2,3,4,6,7,12,14,21,28,42,84}

{1,5,17,85}

{1,2,43,86}

{1,3,29,87}

{1,2,4,8,11,22,44,88}

{1,89}

{1,2,3,5,6,9,10,15,18,30,45,90}

{1,7,13,91}

{1,2,4,23,46,92}

{1,3,31,93}

{1,2,47,94}

{1,5,19,95}

{1,2,3,4,6,8,12,16,24,32,48,96}

{1,97}

{1,2,7,14,49,98}

{1,3,9,11,33,99}

108

123

106

140

144

156

Facteurs

Diviseurs

Quantité

Somme'

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

(2)^2*(5)^2

(101)

(2)*(3)*(17)

(103)

(2)^3*(13)

(3)*(5)*(7)

(2)*(53)

(107)

(2)^2*(3)^3

(109)

(2)*(5)*(11)

(3)*(37)

(2)^4*(7)

(113)

(2)*(3)*(19)

(5)*(23)

(2)^2*(29)

(3)^2*(13)

(2)*(59)

(7)*(17)

(2)^3*(3)*(5)

(11)^2

(2)*(61)

(3)*(41)

(2)^2*(31)

(5)^3

(2)*(3)^2*(7)

(127)

(2)^7

(3)*(43)

(2)*(5)*(13)

(131)

(2)^2*(3)*(11)

(7)*(19)

(2)*(67)

(3)^3*(5)

(2)^3*(17)

(137)

(2)*(3)*(23)

(139)

(2)^2*(5)*(7)

(3)*(47)

(2)*(71)

(11)*(13)

(2)^4*(3)^2

(5)*(29)

(2)*(73)

(3)*(7)^2

(2)^2*(37)

(149)

(2)*(3)*(5)^2

(151)

(2)^3*(19)

(3)^2*(17)

(2)*(7)*(11)

(5)*(31)

(2)^2*(3)*(13)

(157)

(2)*(79)

(3)*(53)

(2)^5*(5)

(7)*(23)

(2)*(3)^4

(163)

(2)^2*(41)

(3)*(5)*(11)

(2)*(83)

(167)

(2)^3*(3)*(7)

(13)^2

(2)*(5)*(17)

(3)^2*(19)

(2)^2*(43)

(173)

(2)*(3)*(29)

(5)^2*(7)

(2)^4*(11)

(3)*(59)

(2)*(89)

(179)

(2)^2*(3)^2*(5)

(181)

(2)*(7)*(13)

(3)*(61)

(2)^3*(23)

(5)*(37)

(2)*(3)*(31)

(11)*(17)

(2)^2*(47)

(3)^3*(7)

(2)*(5)*(19)

(191)

(2)^6*(3)

(193)

(2)*(97)

(3)*(5)*(13)

(2)^2*(7)^2

(197)

(2)*(3)^2*(11)

(199)

{1,2,4,5,10,20,25,50,100}

{1,101}

{1,2,3,6,17,34,51,102}

{1,103}

{1,2,4,8,13,26,52,104}

{1,3,5,7,15,21,35,105}

{1,2,53,106}

{1,107}

{1,2,3,4,6,9,12,18,27,36,54,108}

{1,109}

{1,2,5,10,11,22,55,110}

{1,3,37,111}

{1,2,4,7,8,14,16,28,56,112}

{1,113}

{1,2,3,6,19,38,57,114}

{1,5,23,115}

{1,2,4,29,58,116}

{1,3,9,13,39,117}

{1,2,59,118}

{1,7,17,119}

{1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120}

{1,11,121}

{1,2,61,122}

{1,3,41,123}

{1,2,4,31,62,124}

{1,5,25,125}

{1,2,3,6,7,9,14,18,21,42,63,126}

{1,127}

{1,2,4,8,16,32,64,128}

{1,3,43,129}

{1,2,5,10,13,26,65,130}

{1,131}

{1,2,3,4,6,11,12,22,33,44,66,132}

{1,7,19,133}

{1,2,67,134}

{1,3,5,9,15,27,45,135}

{1,2,4,8,17,34,68,136}

{1,137}

{1,2,3,6,23,46,69,138}

{1,139}

{1,2,4,5,7,10,14,20,28,35,70,140}

{1,3,47,141}

{1,2,71,142}

{1,11,13,143}

{1,2,3,4,6,8,9,12,16,18,24,36,48,72,144}

{1,5,29,145}

{1,2,73,146}

{1,3,7,21,49,147}

{1,2,4,37,74,148}

{1,149}

{1,2,3,5,6,10,15,25,30,50,75,150}

{1,151}

{1,2,4,8,19,38,76,152}

{1,3,9,17,51,153}

{1,2,7,11,14,22,77,154}

{1,5,31,155}

{1,2,3,4,6,12,13,26,39,52,78,156}

{1,157}

{1,2,79,158}

{1,3,53,159}

{1,2,4,5,8,10,16,20,32,40,80,160}

{1,7,23,161}

{1,2,3,6,9,18,27,54,81,162}

{1,163}

{1,2,4,41,82,164}

{1,3,5,11,15,33,55,165}

{1,2,83,166}

{1,167}

{1,2,3,4,6,7,8,12,14,21,24,28,42,56,84,168}

{1,13,169}

{1,2,5,10,17,34,85,170}

{1,3,9,19,57,171}

{1,2,4,43,86,172}

{1,173}

{1,2,3,6,29,58,87,174}

{1,5,7,25,35,175}

{1,2,4,8,11,16,22,44,88,176}

{1,3,59,177}

{1,2,89,178}

{1,179}

{1,2,3,4,5,6,9,10,12,15,18,20,30,36,45,60,90,180}

{1,181}

{1,2,7,13,14,26,91,182}

{1,3,61,183}

{1,2,4,8,23,46,92,184}

{1,5,37,185}

{1,2,3,6,31,62,93,186}

{1,11,17,187}

{1,2,4,47,94,188}

{1,3,7,9,21,27,63,189}

{1,2,5,10,19,38,95,190}

{1,191}

{1,2,3,4,6,8,12,16,24,32,48,64,96,192}

{1,193}

{1,2,97,194}

{1,3,5,13,15,39,65,195}

{1,2,4,7,14,28,49,98,196}

{1,197}

{1,2,3,6,9,11,18,22,33,66,99,198}

{1,199}

117

114

106

172

106

136

126

240

100

186

127

122

204

105

134

150

196

259

118

222

148

134

236

218

201

130

123

312

154

136

186

196

366

154

176

198

148

131

170

316

100

141

203

270

Facteurs

Diviseurs

Quantité

Somme'

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

289

290

291

292

293

294

295

296

297

298

299

(2)^3*(5)^2

(3)*(67)

(2)*(101)

(7)*(29)

(2)^2*(3)*(17)

(5)*(41)

(2)*(103)

(3)^2*(23)

(2)^4*(13)

(11)*(19)

(2)*(3)*(5)*(7)

(211)

(2)^2*(53)

(3)*(71)

(2)*(107)

(5)*(43)

(2)^3*(3)^3

(7)*(31)

(2)*(109)

(3)*(73)

(2)^2*(5)*(11)

(13)*(17)

(2)*(3)*(37)

(223)

(2)^5*(7)

(3)^2*(5)^2

(2)*(113)

(227)

(2)^2*(3)*(19)

(229)

(2)*(5)*(23)

(3)*(7)*(11)

(2)^3*(29)

(233)

(2)*(3)^2*(13)

(5)*(47)

(2)^2*(59)

(3)*(79)

(2)*(7)*(17)

(239)

(2)^4*(3)*(5)

(241)

(2)*(11)^2

(3)^5

(2)^2*(61)

(5)*(7)^2

(2)*(3)*(41)

(13)*(19)

(2)^3*(31)

(3)*(83)

(2)*(5)^3

(251)

(2)^2*(3)^2*(7)

(11)*(23)

(2)*(127)

(3)*(5)*(17)

(2)^8

(257)

(2)*(3)*(43)

(7)*(37)

(2)^2*(5)*(13)

(3)^2*(29)

(2)*(131)

(263)

(2)^3*(3)*(11)

(5)*(53)

(2)*(7)*(19)

(3)*(89)

(2)^2*(67)

(269)

(2)*(3)^3*(5)

(271)

(2)^4*(17)

(3)*(7)*(13)

(2)*(137)

(5)^2*(11)

(2)^2*(3)*(23)

(277)

(2)*(139)

(3)^2*(31)

(2)^3*(5)*(7)

(281)

(2)*(3)*(47)

(283)

(2)^2*(71)

(3)*(5)*(19)

(2)*(11)*(13)

(7)*(41)

(2)^5*(3)^2

(17)^2

(2)*(5)*(29)

(3)*(97)

(2)^2*(73)

(293)

(2)*(3)*(7)^2

(5)*(59)

(2)^3*(37)

(3)^3*(11)

(2)*(149)

(13)*(23)

{1,2,4,5,8,10,20,25,40,50,100,200}

{1,3,67,201}

{1,2,101,202}

{1,7,29,203}

{1,2,3,4,6,12,17,34,51,68,102,204}

{1,5,41,205}

{1,2,103,206}

{1,3,9,23,69,207}

{1,2,4,8,13,16,26,52,104,208}

{1,11,19,209}

{1,2,3,5,6,7,10,14,15,21,30,35,42,70,105,210}

{1,211}

{1,2,4,53,106,212}

{1,3,71,213}

{1,2,107,214}

{1,5,43,215}

{1,2,3,4,6,8,9,12,18,24,27,36,54,72,108,216}

{1,7,31,217}

{1,2,109,218}

{1,3,73,219}

{1,2,4,5,10,11,20,22,44,55,110,220}

{1,13,17,221}

{1,2,3,6,37,74,111,222}

{1,223}

{1,2,4,7,8,14,16,28,32,56,112,224}

{1,3,5,9,15,25,45,75,225}

{1,2,113,226}

{1,227}

{1,2,3,4,6,12,19,38,57,76,114,228}

{1,229}

{1,2,5,10,23,46,115,230}

{1,3,7,11,21,33,77,231}

{1,2,4,8,29,58,116,232}

{1,233}

{1,2,3,6,9,13,18,26,39,78,117,234}

{1,5,47,235}

{1,2,4,59,118,236}

{1,3,79,237}

{1,2,7,14,17,34,119,238}

{1,239}

{1,2,3,4,5,6,8,10,12,15,16,20,24,30,40,48,60,80,120,240}

{1,241}

{1,2,11,22,121,242}

{1,3,9,27,81,243}

{1,2,4,61,122,244}

{1,5,7,35,49,245}

{1,2,3,6,41,82,123,246}

{1,13,19,247}

{1,2,4,8,31,62,124,248}

{1,3,83,249}

{1,2,5,10,25,50,125,250}

{1,251}

{1,2,3,4,6,7,9,12,14,18,21,28,36,42,63,84,126,252}

{1,11,23,253}

{1,2,127,254}

{1,3,5,15,17,51,85,255}

{1,2,4,8,16,32,64,128,256}

{1,257}

{1,2,3,6,43,86,129,258}

{1,7,37,259}

{1,2,4,5,10,13,20,26,52,65,130,260}

{1,3,9,29,87,261}

{1,2,131,262}

{1,263}

{1,2,3,4,6,8,11,12,22,24,33,44,66,88,132,264}

{1,5,53,265}

{1,2,7,14,19,38,133,266}

{1,3,89,267}

{1,2,4,67,134,268}

{1,269}

{1,2,3,5,6,9,10,15,18,27,30,45,54,90,135,270}

{1,271}

{1,2,4,8,16,17,34,68,136,272}

{1,3,7,13,21,39,91,273}

{1,2,137,274}

{1,5,11,25,55,275}

{1,2,3,4,6,12,23,46,69,92,138,276}

{1,277}

{1,2,139,278}

{1,3,9,31,93,279}

{1,2,4,5,7,8,10,14,20,28,35,40,56,70,140,280}

{1,281}

{1,2,3,6,47,94,141,282}

{1,283}

{1,2,4,71,142,284}

{1,3,5,15,19,57,95,285}

{1,2,11,13,22,26,143,286}

{1,7,41,287}

{1,2,3,4,6,8,9,12,16,18,24,32,36,48,72,96,144,288}

{1,17,289}

{1,2,5,10,29,58,145,290}

{1,3,97,291}

{1,2,4,73,146,292}

{1,293}

{1,2,3,6,7,14,21,42,49,98,147,294}

{1,5,59,295}

{1,2,4,8,37,74,148,296}

{1,3,9,11,27,33,99,297}

{1,2,149,298}

{1,13,23,299}

265

104

300

106

105

226

366

166

110

384

112

284

234

280

178

116

332

202

153

218

312

184

194

504

157

121

190

258

232

218

476

130

177

255

270

328

129

134

456

214

208

450

286

175

140

396

142

137

440

294

220

195

218

531

250

101

226

390

274

183

152

Suite	De 300 à 1000
Voir	Tables – Index
DicoNombre	Orientation vers tous les nombres du dictionnaire
Site	OEIS A088076 – Smallest prime sandwiched between two numbers having exactly n prime divisors OEIS A088075 – Smallest number sandwiched between two numbers having exactly n prime divisors.
Cette page	http://villemin.gerard.free.fr/TABLES/Facteurs.htm