|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
NOMBRES PARFAITS
Cool SVP!
Voir
Débutant |
Anglais: Perfect numbers
Selon
la somme par rapport au nombre
Rappel, vous pouvez
consulter la Page débutants
Un petit avant-goût!
|
Voici
la physionomie d'un nombre parfait*: une puissance
k-1 de deux multipliée par une puissance k de deux moins 1. Si ce deuxième
facteur (nombre de Mersenne) est premier alors le nombre est parfait.
Notez
la ressemblance des facteurs en puissance de deux: le "moins un"
est soit dans l'exposant soit en soustraction. *
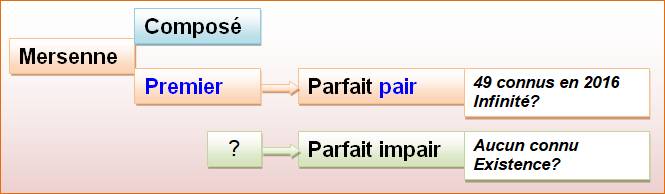
Tous les parfaits pairs sont
de cette forme. On ne sait pas s'il existe des nombres parfaits
impairs. |
|
|
||
|
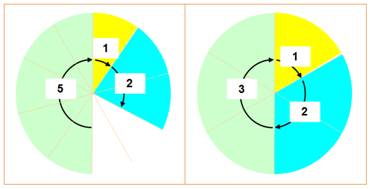
n = 10 est divisible par
1, 2 et 5 |
n = 6 est divisible par
1, 2 et 3 |
|
|
Le plateau est
divisé n parts. On prend les parts
selon les diviseurs.
|
||
|
La somme des parts
est plus petite que 10
parts. C'est un nombre déficient. |
La somme des parts
est justement 6. C'est un nombre parfait. |
|
|
|
|||||||||||||
|
Définition NOMBRE PARFAIT: nombre
égal à la somme de ses diviseurs propres. Exemples
À noter ·
On note que la somme des diviseurs
( Alors
que la somme des diviseurs propres ( ·
Soit la relation: ·
Or pour un nombre parfait, selon sa définition: ·
En remplaçant, on trouve pour un nombre parfait: NOMBRE PARFAIT: nombre
dont la somme des diviseurs vaut le
double du nombre. ·
À ce titre les nombres parfaits pourraient être
baptisés bi-parfait. |
|||||||||||||
|
|
|
|
6 = 1 + 2 + 3 28 = 1 + 2 + 3 + ... + 7 496 = 1 + 2 + 3 + ... + 31 8
128 = 1 + 2 + 3 + ... + 127 Etc. Tous les nombres parfaits sont la somme des cubes des nombres impairs consécutifs. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Si N = 2n-1
( 2n – 1) avec p = (2n – 1) premier, alors N est parfait. ·
Tous les nombres parfaits connus aujourd'hui répondent
à la formule d'Euclide. Léonard Euler
(1707-1783) a démontré que tous les parfaits pairs sont
de ce type. ·
On ne sait toujours pas s'il existe des nombres
parfaits impairs (testé jusqu'à 10150). ·
Une puissance de deux moins
un est un nombre de Mersenne. Voir Démonstration / Divisibilité
/ Exemple avec modulo Exemples
Binaire ·
Impliquant des puissances de 2, il n'est pas surprenant
que les nombres parfaits prennent une forme sympathique en binaire: 6 28 496 8 128 Historique ·
Euclide avait trouvé cette formule. Euler démontre la
réciproque (1749): ·
Il montre que tous les nombres parfaits
pairs sont de cette forme. ·
Or, on ne connaît que des
nombres parfaits pairs ·
Il se trouve que (2n – 1) est un nombre
de Mersenne et, les nombres de Mersenne ne sont premiers que si n lui-même est premier. ·
Pour n = 3, on a: 2n – 1 = 8 –
1 = 7, premier et N = 4 x 7 = 28 ·
Pour n = 4, on a: 2n – 1 = 16
– 1 = 15, composé ·
Pour n = 5, on a: 2n – 1 = 32
– 1 = 31, premier et N = 16 x 31 = 496 ·
En 1963, à l'Université de l'Illinois, on a trouvé un
nombre parfait pour n
= 11 213 qui s'exprime avec 6 751 chiffres et se décompose en 22 425
diviseurs. C'était le nombre parfait n°23. ·
En 2016, on a trouvé le Mersenne premier n°49 qui est
aussi le nombre premier le plus grand que l'on connaisse. Voir Liste des nombres parfaits / Record du plus grand premier / Historique des nombres de Mersenne N est un nombre parfait si et seulment s'il est de la forme 2p-1
(2p – 1 ) et si (2p – 1) est premier. si (2p
– 1) est premier, alors p est lui-même premier. Illustration
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Infinité ? Il y a une infinité de nombres
parfaits. ·
Les nombres parfaits sont rares. On en connaît
seulement 49, autant que de Mersenne
premiers connus. On connait bien tous les nombres de Mersenne premiers
successifs jusqu'au 45e.
Voir Liste ·
On ne pas si les nombres parfaits sont en nombre infini.
Probablement oui, car la série harmonique diverge. ·
Existe-t-il une infinité de nombres de Mersenne
composés ? Euler a montré que : ·
Si k > 1
et p = 4k + 3 est
premier, alors 2p + 1
est premier si et seulement si 2p
= 1 (mod 2p + 1). 6 et 28 Tous les nombres parfaits pairs se
terminent par 6
ou 28. ·
Tous les nombres parfaits se terminent par 6 ou 28. La
séquence du chiffre final semble vouloir nous dire quelque chose, mais n'est
pas régulière: Racine numérique La racine numérique (ou preuve par 9) des nombres
parfaits est égale à 1 (sauf
pour 6). Exemple: 28 Inverses La somme des inverses des diviseurs
d'un nombre parfait est égale à 2. Exemple: 1/1 + 1/2 + 1/4 +
1/7 + 1/14 + 1/28 = 2 ·
Cette propriété n'est pas magique! Essayez de réduire au même dénominateur et
vous verrez. Conjecture Il n'existe pas de nombres parfaits
impairs. ·
S'il existe des nombres parfaits impairs, ils doivent
être très grands (au moins 300 chiffres) - Brent et Cohen (1989). ·
On sait que, divisé par 12, il reste 1, ·
Et divisé par 36, il reste 9; ·
Ils ont au moins 6 facteurs premiers; ·
Etc. ·
C'est un carré, multiplié par une puissance impaire
d'un nombre premier seul. ·
Il est divisible par au moins 8 premiers. ·
il a au moins 29 facteurs premiers (pas nécessairement
distincts). ·
Il a un diviseur premier plus grand que 1020. Harmonique : ·
Tous les nombres parfaits
sont harmoniques: la
moyenne harmonique des diviseurs est un nombre entier. Quantité de chiffres ·
Le ratio entre p (la puissance de 2) et la quantité de
chiffres Q du nombre parfait approche log(10) / log(4) = 1,660964048… |
|
Anecdote
|
· René Descartes
pensait avoir découvert un nombre parfait impair, sauf que
22 021 n'est pas premier. On ne connaît toujours pas de nombre parfait impair
à ce jour. |
|
|
Décomposition de Descartes |
N = 32 . 72 . 112
. 132 . 22 021 = 198 585 576 189 |
|
= 397 171 152 378 = 2 x 198 585 576 189 |
|
|
Véritable décomposition |
N = 32 . 72 . 112
. 132 . 192 . 61 |
|
Somme des diviseurs |
= 426 027 470 778 ·
N n'est pas
parfait, il est abondant |
Voir Nombre
198 585 576 189
|
|
|||||||||
|
Voyons les premiers nombres parfaits, décomposés en
facteurs partiels:
Ils sont tous
le produit d'une puissance de 2 et de la puissance suivante de 2 moins 1,
comme 4 x 7 = 22 x (23 – 1). En fait, ils sont de la
forme 2n
– 1 (2n – 1) et chaque 2n
– 1 est un
nombre premier
de Mersenne. Théorème 1 k est un nombre
parfait pair, si et seulement si, il est de la forme 2n – 1 (2n
– 1) avec 2n
– 1 premier (premier de Mersenne). Théorème 2 Si 2n
– 1 est premier, alors n est premier. La recherche des
nombres de Mersenne est aussi celle des nombres parfaits pairs. Théorème 3 Soit p et q
premiers. Si divise Mp
= 2p – 1, alors q = pour quelques
valeurs entières de k. Théorème 4 Soit p =
3 (mod
4),
un
premier. 2p + 1 est aussi un premier
si et seulement si 2p + 1 divise Mp. |
|||||||||
Theorems
|
Theorem
One:
k
is an even perfect number if and only if it has the form 2n-1(2n
– 1) and 2n – 1 is prime. Theorem Two: If 2n – 1 is prime, then so is
n. |
|
|
||
|
·
Dans le cas d'un nombre
triparfait, la somme des diviseurs, y compris lui-même, est égale à trois fois le nombre: Cas de 120 = 23 . 3 . 5
et la somme de tous ses diviseurs: 1
+ 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 3 x 120. ·
Les triparfaits sont tous pairs. S'il en existe un impair, il est
supérieur à 1050. ·
On ne connaît que six nombres triparfaits: |
||
|
120 672 523 776 459 818
240 1 476
304 896 51 001
180 160 |
=
23 x 3 x 5 (Mersenne
1557) =
25 x 3 x 7 (Fermat 1636) =
29 × 3 × 11 × 31 = 28 × 5 × 7 × 19 ×
37 × 73 = 213 × 3 × 11 × 43
× 127 = 214 × 5 × 7 × 19 ×
31 × 151 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Définition ·
La somme des diviseurs, y compris lui-même, fait k
fois le nombre: n est appelé k-parfait. · On connaît plus de
500 nombres multiparfaits jusqu'à l'ordre 8. On conjecture qu'il existe des
nombres k-parfait pour toutes les valeurs de k. ·
25 x 33 x 5 x 7 est le premier
tétraparfait. ·
27 x 34 x 5 x 7 x 11² x 17 x 19,
le premier pentaparfait. Quelques multiparfaits
Pn
Quantité minimum de facteurs
premiers distincts
Lehmer 1901 Quantité de nombre
multiparfaits connus
·
On pense connaître tous les multiparfaits d'ordre 3, 4,
5, 6 et 7. Le plus grand connu De l'ordre de 7,3 10 1 345 Moxham -
Février 2000 |
|||||||||||||||||||||||||||||||||||||||
Multi ou hyper ?
|
|
Nombres multiparfaits harmoniques
|
Nombres
égaux à n fois le rapport entre la quantité de diviseurs et la somme des
diviseurs propres:
Exemple:
H(140)
= 140 x 12 / 336 = 5 Liste 1,
140, 270, 672, 1638, 2970, 6200, 8190, 18600, 18620, 27846, 30240, 32760,
55860, 105664, 117800, 167400, 173600, 237510, 242060, 332640, 360360,
539400, 695520, 726180, 753480, 950976, 1089270, 1421280, 1539720, … Voir Nombres
d'Ore (semblables) Programmation Maple
|
Voir OEIS
A090945 / Programmation – Index
|
|
||
|
Définition Un nombre
k-hyperparfait est tel que:
Un nombre
1-hyperparfait est un nombre parfait: Un nombre
2-hyperparfait (2-HP) est de la forme: Un nombre
3-hyperparfait (2-HP) est de la forme: Relations
|
Listes 2-HP: 21, 2 133, 19 521, 176
661, Ex: 3-HP: 325, aucun autre jusqu'à n = 1
000 000 4-HP: 1 950 625, 1 222 640 625, 5-HP: aucun connu 6-HP: 301, 16 513, 60 110 701, 10-HP: 159 841 11-HP: 10 693 12-HP: 697, 2 041, 1
570 153, 62 722 153, 10 604 156 641, 13 544 168 521, 1 792 155 938 521 18-HP: 1 333, 1 909, 24
69 601, 893 748 277, 322 685 352 001, 8 992 165 119 733, 42 052 982 615 431
201 |
|
|
|
||
|
Nombres égaux à la somme des diviseurs retournés
(lus de droite à gauche). |
Exemple Diviseurs de 244: 1, 2, 4, 61, 122 Retournés: 1, 2, 4, 16, 221 Somme: 244 Liste des cinq connus 6, 244,
285, 133
857, 141
635 817. |
|
Anglais: anti-perfact numbers
|
|
|
|
A positive integer
n is called a perfect number if it is equal to the sum of all of its positive
divisors, excluding n itself. |
|
Grand merci à Maximilian pour ses remarques
|
Suite |
·
Programmation de la recherche
des parfaits ·
Traité
sur les nombres parfaits · Nombres
parfaits – Théorie des nombres |
|
Voir |
·
Calcul mental
– Index ·
Démonstration de la formule
d'Euclide ·
Géométrie
– Index ·
Nombres économes,
équidistants et prodigues · Tables abondants / déficients · Théorie des
nombres – Index |
|
DicoNombre |
·
Nombre
1,66… ·
Nombre
198 585 576 189 |
|
Sites |
·
Nombre hyperparfaits
– Wikipédia ·
Répartition des nombres
superabondants par Paul Erdös et JL Nicolas – Définition
des nombres hautement composés et superabondants. · Prefect number –
Wolfram MathWorld · Mersenne
Primes: History, Theorems and List – Chris Caldwell · A Study of
Hyperperfect Numbers – Judson McCranie – 2000 – Très complet avec listes et references. · OEIS A007593
- 2-hyperperfect numbers: n = 2*(sigma(n) - n - 1) + 1. · OEIS A028500
– 12-hyperperfect numbers: n = 12*(sigma(n) - n - 1) + 1 |
|
Cette page |
