|
||||||||||||
![]()
|
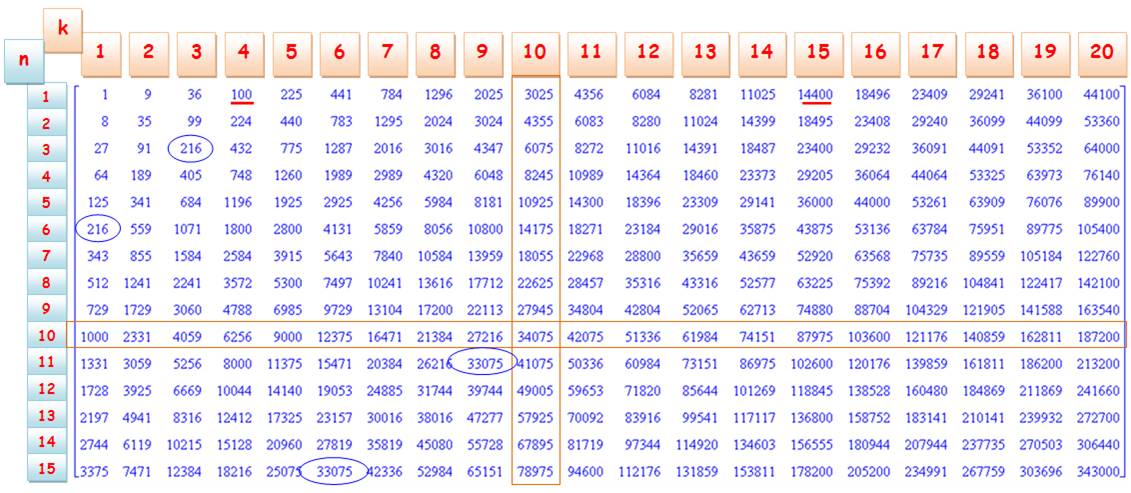
TABLE: Somme des cubes de k nombres consécutifs à partir de n Sn = n3 + (n+1)3
+ … (n+k)3 Exemples: 23 + 33 + 43 + 53
+ 63 = 440 (5
termes) 153 +
163 + … + 343
= 343 000 (20 termes) |
Voir Somme des cubes de nombres
consécutifs
|
|
|
|
Exemple de lecture: n = 2 et k = 3, on lit 99 car c'est la somme de trois (k = 3) cubes
consécutifs en commençant par 2 (n = 2) :
23 + 33
+ 43 = 99.
Notes On se souvient que: 13 + 23 + 33 +
43 = 100. On note: 13 + 23 + 33
+ … + 153 = 144
000 = 120². Les valeurs entourées sont deux égalités: 33
+ 43 + 53 = 63 = 216
et
153 + 163 + … + 203 = 113 + 123
+ … + 193 = 33 075. La colonne de vingt termes de suite se
termine par au moins un 0; parfois trois 0. La colonne de dix termes de suite se termine
par au moins un 5. Normal! Sur dix termes la somme des unités des cubes est
toujours: 1, 8, 7, 4, 5, 6, 3, 2, 9, 0 dont la somme vaut 45; et voilà notre
5 pour dix termes. Et une somme de 90
pour vingt termes; et voilà notre 0 systématique en dernière colonne à
droite. |
|
|
|
|
|
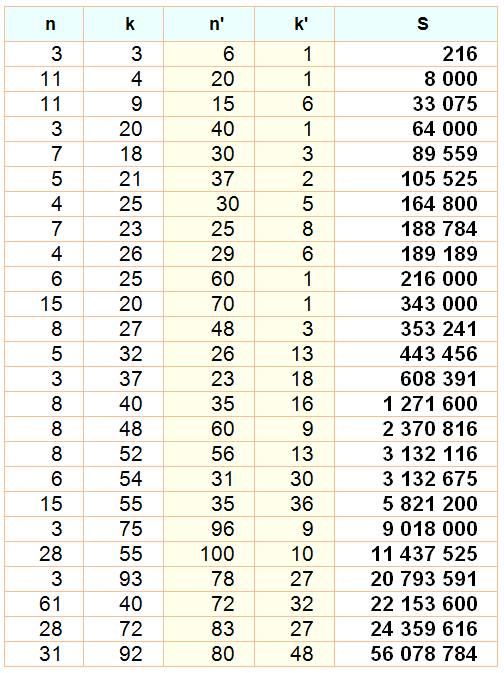
Nous retrouvons les égalités ci-dessus dans
le tableau ci-dessous. La première 33 + 43 +
53 = 63 = 216. La seconde est nouvelle: 113 + 123
+ 133 + 143 = 203 = 8 000. La troisième est celle remarquée plus haut.
153 + 163 + … + 203
= 113 + 123 + … + 193 = 33 075. La suivante est également un cube: 403
= 33 + 43 + … +
223 = 64 000.
|
|
![]()
|
Suite |
|
|
Diconombre |
|
|
Voir |
|
|
Cette page |
![]()