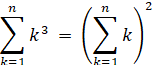|
|||||||||||||||||||||||||||||||||
![]()
|
SOMME des NOMBRES Démonstrations par induction Le
principe est simple: si la propriété est vraie au départ et si elle est vraie
pour tout successeur, alors elle est vraie pour tout le monde. |
Voir Démonstration
par induction
|
|
||
|
Affirmation: somme des entiers |
1 + 2 + … + n = ½ n (n + 1) = Tn Tn = nombre
triangulaire |
|
|
Démonstration par
induction |
||
|
Pour n =1, C'est vrai. |
1 = ½ x 1 (1 + 1) |
|
|
Supposons la
formule vraie pour n. L'est-elle pour n
+ 1? Effectivement,
nous retrouvons bien la formule avec n remplacé par n+1. |
1 + 2 + … + n + (n + 1) = ½ n (n + 1) + (n + 1) = ½ { (n² + n) + (2n + 2) = ½ { n² + 3n + 2 } = ½ { n (n +1) + 2 (n + 1) } = ½ (n + 1) (n + 2) |
|
|
Exemple n = 9 |
1+2+3+4+5+6+7+8+9 = ½ x 9 x 10 = 45 |
|
|
Extension à la somme
des pairs et
autres multiples Même
principe pour les multiples de 3 ou de k. |
2 + 4 + … + 2n = 2 (1 + 2 + … + n) = 2 x { ½ n(n + 1) } = n (n + 1) |
|
|
Exemple n = 4
(jusqu'au nombre pair 8) |
2 + 4 + 6 + 8 = 4
x 5 = 20 |
|
|
Extension à la somme
des impairs |
1 + 3 + … + (2n – 1) = 2 + 4 + … + 2n –1 – 1
– … – 1 = n (n + 1) – n = n² |
|
|
Exemple n = 4
(jusqu'au nombre impair 7) |
1 + 3 = 4 = 2² 1 + 3 + 5 =
9 = 3² 1 + 3 + 5 +
7 = 16 = 4² |
|
Voir Sommes des nombres
pairs / des
impairs
Merci à Julien P. et Christian A.
|
|
||
|
Affirmation: somme des carrés |
1² + 2² + … +
n² = 1/6 n (n + 1) (2n + 1) |
|
|
Pour n =1, C'est vrai. |
1 = 1/6 x 1 (1 + 1) (2 + 1) |
|
|
Supposons la
formule vraie pour n. L'est-elle pour n
+ 1? Effectivement
nous retrouvons bien la formule avec n remplacé par n+1. Évidemment la
conduite des opérations est guidée par la connaissance du résultat à obtenir. |
1² + 2² + … + n² + (n + 1)² = 1/6 n (n + 1) (2n
+ 1) + (n + 1)² = 1/6 { n (n + 1) (2n + 1) + 6 (n + 1)² } = 1/6 { (n + 1) (2n² + n) + 6n² + 12n + 6 } = 1/6 { (n + 1) (2n² + n) + 6n (n + 1) + 6 (n+ 1) } = 1/6 { (n + 1) (2n² + n) + (n + 1) ( 6n + 6) } = 1/6 (n + 1) (2n² + n + 6n + 6) = 1/6 (n + 1) { 2n (n + 2 ) + 3 (n + 2) } = 1/6 (n + 1) (n + 2 ) (2n + 3) |
|
|
Exemple n = 3 |
1² + 2² + 3² =
1/6 x 3 x 4 x 7 = 14 = 1 + 4 + 9 |
|
Voir Nombres carrés / Démonstration par différences finies / Nombres pyramidaux carrés
|
|
|||
|
Affirmation: somme des cubes Voir Cubes |
13 + 23 +
… + n3 = { ½ n (n + 1) } ² = {1
+ 2 + ... + n} ² Notez la
ressemblance avec la somme des entiers |
||
|
Notation compacte |
|
||
|
Exemple typique |
10 = 1 + 2 + 3 + 4 100
= 10² = (1 + 2 + 3 + 4)2 = 13 + 23 + 33
+ 43 |
||
|
Nicomaque de Gérase (60 à 120 ?) Gérase en Jordanie |
Introduction à
l'arithmétique:
Il remarque qu'en
ajoutant les nombres impairs par paquets (1, 3 + 5, 7 + 9 + 11, 13 + 15 + 17
+ 19…), on obtient les cubes successifs des entiers naturels (13, 23, 33, 43…). |
||
|
Démonstration par
induction |
|
||
|
Pour n =1, C'est vrai. |
1 = { ½ x 1 (1 + 1) }² |
||
|
Supposons la
formule vraie pour n. L'est-elle pour n
+ 1? Effectivement
nous retrouvons bien la formule avec n remplacé par n+1. |
13 + 23 + … + n3 + (n + 1)3 = { ½ n (n + 1) } ² + (n + 1)3 = ¼ { n² (n + 1)² + 4 (n + 1)3 } = ¼ { n4 + 2n3 + n2 + 4n3 + 12n2 + 12n + 4 } = ¼ { n4 + 6n3 + 13n2 + 12n + 4 } = ¼ { n² (n² + 2n + 1) + 4n (n² + 2n + 1)
= ¼ { (n² + 2n + 1) (n² + 4n + 4) } = ¼ { (n + 1)² (n + 2)² } |
||
|
Exemple n = 3 |
13 + 23 + 33 = (1/2 x 3 x 4)² = 6² = 36 = 1 + 8 + 27 |
||
|
Somme
des NOMBRES successifs au cube pour k de 1 à 50 |
1, 9, 36, 100, 225, 441,
784, 1296, 2025, 3025, 4356, 6084, 8281, 11025, 14400, 18496, 23409, 29241,
36100, 44100, 53361, 64009, 76176, 90000, 105625, 123201, 142884, 164836,
189225, 216225, 246016, 278784, 314721, 354025, 396900, 443556, 494209,
549081, 608400, 672400, 741321, 815409, 894916, 980100, 1071225, 1168561,
1272384, 1382976, 1500625, 1625625, ... |
||
Voir Carré = Somme de
cubes (suite) / Démonstration par différences finies
/ Somme de cubes – Table
|
|
|||
|
La somme des
cubes est égale à la somme des impairs et des pairs. Somme des n = 2k
premiers nombres. |
13 + 23 + 33
+ … + (2k – 1)3 + (2k)3
=
13 + 33 +
… + (2k – 1)3 + 23 + … + (2k)3 |
||
|
Écriture
simplifiée. Somme des nombres pairs de 1 à n = 2k Somme des nombres impairs de 1 à m = 2k – 1. |
S2k = P2k
+ I2k-1 |
||
|
Or la somme des
pairs peut s'exprimer en fonction de celle des entiers |
P2k
= 23 + 43 + … + (2k)3 =
23 (13 + 23 + … + k3 ) = 23 Sk |
||
|
Exprimons la
somme des cubes des impairs |
I2k-1 = S2k – P2k = S2k – 23 Sk |
||
|
Autrement dit,
avec la formule de la somme des cubes: Sk = 1/4
(k (k + 1))² S2k =
1/4 (2k (2k + 1))² |
I2k-1 = 1/4 (2k(2k+1))²
– 8/4 (k(k+1))² = 1/4 (4k²(4k²+4k+1) – 8k²(k²+2k+1)) = 4k4+4k3+k2
– 2k4–4k3–2k2 = 2k4 – k2 = k² (2k2 – 1) |
||
|
Exemple avec k = 2, soit deux termes |
I2x2-1
= I3 = 2² (2x2² – 1) = 4x7
= 28 = 13 + 33 = 1 + 27
= 28 |
||
|
k = 3, soit trois termes |
I5 = 3² (2x3² – 1) = 9x17 = 153 = 13 + 33 + 53
= 153 |
||
|
Somme
des IMPAIRS successifs au cube pour k de 1 à 50 |
1, 28, 153, 496, 1225,
2556, 4753, 8128, 13041, 19900, 29161, 41328, 56953, 76636, 101025, 130816,
166753, 209628, 260281, 319600, 388521, 468028, 559153, 662976, 780625,
913276, 1062153, 1228528, 1413721, 1619100, 1846081, 2096128, 2370753,
2671516, 3000025, 3357936, 3746953, 4168828, 4625361, 5118400, 5649841,
6221628, 6835753, 7494256, 8199225, 8952796, 9757153, 10614528, 11527201,
12497500, ... |
||
|
Somme
des PAIRS successifs au cube pour k de 1 à 50 |
8, 72, 288, 800, 1800, 3528, 6272, 10368, 16200, 24200,
34848, 48672, 66248, 88200, 115200, 147968, 187272, 233928, 288800, 352800,
426888, 512072, 609408, 720000, 845000, 985608, 1143072, 1318688, 1513800,
1729800, 1968128, 2230272, 2517768, 2832200, 3175200, 3548448, 3953672,
4392648, 4867200, 5379200, 5930568, 6523272, 7159328, 7840800, 8569800,
9348488, 10179072, 11063808, 12005000, 13005000, ... |
||
|
|
||
|
Affirmation: cube = diférence de deux carrés |
n3 =
a² – b² |
|
|
Démonstr |
|
|
|
Écrivons
simplement cette égalité |
n3
= { 13 + 23 + … + n3 } - { 13 + 23 + … +
(n – 1)3 } |
|
|
Exprimons les
deux termes comme la somme des cubes |
n3
= { ½ n (n+1) }² - { ½ (n – 1) n }² |
|
|
Exemple |
43 = { ½ x 20}² - { ½ x 12}² = 10² - 6² = 100 – 36 = 64 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomDemo1.htm
|
![]()