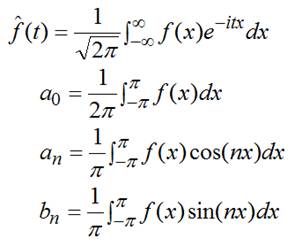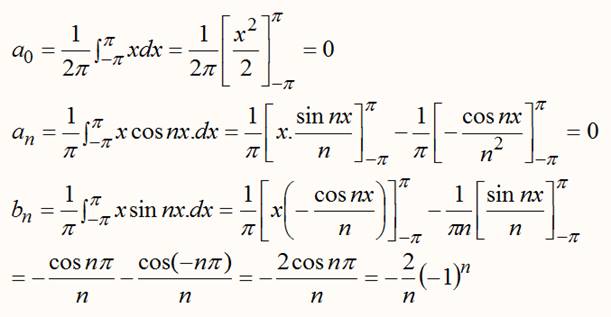|
||||||||||||||||||||
![]()
FFT: le prisme mathématique de la dispersion des ondes
|
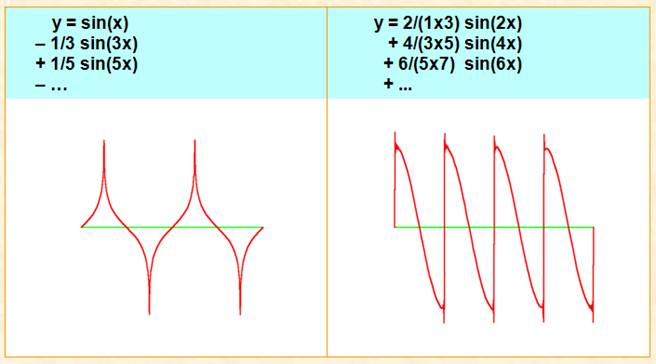
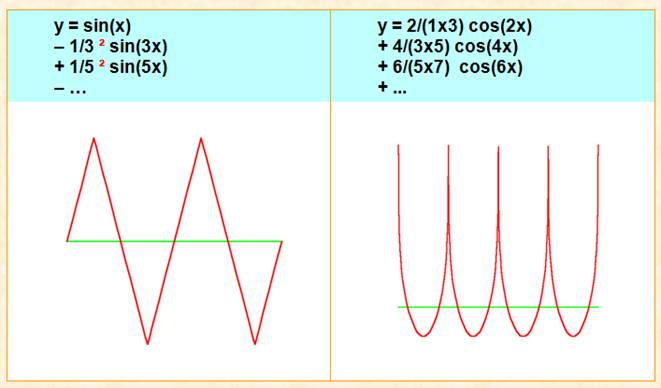
SÉRIE DE FOURIER TRANSFORMÉE DE FOURIER Outil pratique qui permet de
faire des calculs sur des Dans un mémoire daté de 1807, Joseph FOURIER,
mathématicien français, affirma, qu’il était possible, dans certaines
conditions, de décomposer une fonction périodique sous la forme d’une somme
infinie de signaux sinusoïdaux. Il est plus facile de connaître
les propriétés de la fonction en analysant les propriétés de chacune des
composantes. Encore une histoire de changement de monde permettant
d'aborder un problème plus simplement… |
Anglais :
Fourier Series / Fourier Transform
|
|
|
|
|
|
|
|
|
Voir Ondes
|
|
||
|
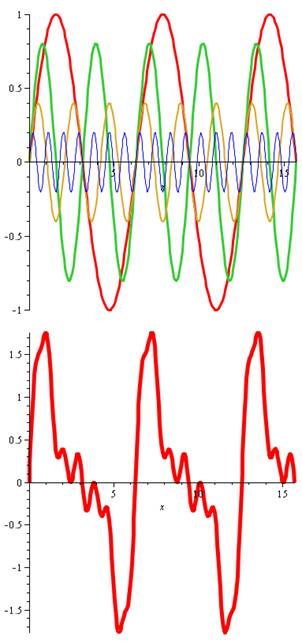
sin(
x) en rouge, 0,8 sin (2x) en vert, 0,4 sin (3x) en jaune, et 0,2 sin (7x) en bleu.
il est possible
d'obtenir une approximation d'une onde quelconque. |
|
|
|
Effet de la phase Tous les
paramètres sont ceux vus ci-dessus sauf pour la deuxième courbe en 2x qui
devient: Soit un
déphasage d'un quart de tour (Pi/2). |
|
|
|
|
|
|
|
|
|
|
|
|
La transformée de Fourier.
La transformée de Fourier rapide FFT: Fast Fourier Transform. Ce que disait Fourier
|
|
Biblio très complète
sur ce sujet : Fourier -
Créateur de la physique mathématique
|
|
f(x) = |
||
|
|
|
a0 |
|
|
|
+ a1
cos x + b1 sin x |
||
|
|
+ a2
cos 2x + b2 sin 2x +… + an cos (n.x) + bn sin
(n.x) +… |
||
|
qui se prêteraient bien à une interprétation en nombres complexes.
|
an et bn
nombres réels cn =
an e+ i . bn
|
|
DROITE
en Fourier |
|
|
|
Fonction |
f(x) = x dans l'intervalle: |
|
|
Détermination des coefficients |
Le calcul est donné à titre indicatif; il dépasse
de loin le cadre de ce site. |
|
|
Soit |
x = 2 sinx – sin2x + 2/3
sin3x – 1/2 sin4x + … |
|
|
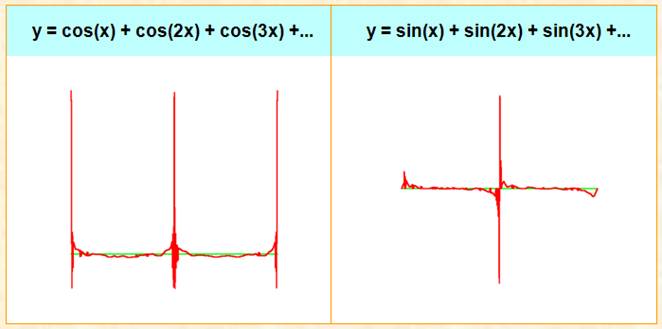
Illustration selon
la quantité de coefficients |
|
|
|
|
|
La transformée de Fourier est un bon outil pour
tous ceux qui ont à traiter des signaux périodiques, ou des fonctions
intégrables. Elle décompose celles-ci en leur spectre
de fréquences élémentaires. Les coefficients obtenus sont appelés séries de Fourier. L'étude des
fonctions par cette méthode s'appelle l'analyse
harmonique. Une façon de décrire les fonctions périodiques. La
fonction est:
Cet outil, y
compris la transformée de Fourier rapide (FFT), sont utilisés en traitement
du signal: radar, sonar, communication, analyse d'images … L'analyse de
spectre en radar ou en sonar
est l'outil principal de la classification
qui permet l'identification d'un contact par sa signature
spectrale (sorte d'empreintes digitales).
|
Voir
Spectre
|
ENGLISH
CORNER |
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()
|
|
|
|
|
|