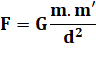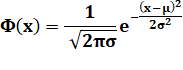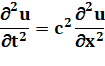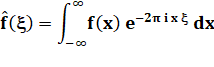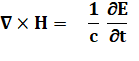|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Les 17 équations qui ont changé le monde par Ian Stewart (traduction: Anatole Muchnik) La présence d'une équation dans
un livre affaiblit la vente du livre,
dit-on. Ian Stewart réussit ce tour de force de nous en présenter dix-sept dans
son livre, certaines sont d'un niveau d'études supérieures. Les équations sont la
transition, la passerelle, entre le monde complexe et une certaine
modélisation compréhensible et manipulable par l'homme. Ian Stewart nous dit
que dix-sept d'entre-elles, présentées dans l'ordre chronologique, décrivent
l'ascension scientifique de l'humanité. La liste proposée pourrait être
complétée par bien d'autres selon le jugement de
chacun. |
|
In pursuit of the Unknown: 17
Equations that changed the World – Ian Stewart Résumé
du livre dans un article de Sciences et Avenir (N°808 de juin 2014). De très nombreuses
reprises sur Internet (anglais).
A collaboré avec Terry
Pratchett (Auteur du Disque-monde) pour l'écriture des trois livres Science
of Discworld. |
Voir Les Grands Maîtres
|
|
|||
|
Théorème de Pythagore |
Permet le calcul de la longueur d'un côté d'un triangle rectangle
lorsqu'on connait la longueur des deux autres. Application très courante en géométrie. 1 >>> |
-530. Pythagore |
|
|
Logarithmes |
Permet le calcul sur des grandeurs de grande amplitude. Passage obligé
avant l'avènement des calculateurs. 2 >>> |
1610 John Napier |
|
|
Calcul différentiel |
Permet le calcul de grandeurs (surface, volume, vitesse …) qui ne sont
appréhendables que par petits pas. 3 >>> |
vers 1668 Newton et Leibniz |
|
|
Loi de gravitation |
Tous les objets ayant une masse s'attirent mutuellement. C'est le cas
de la Terre qui nous maintient à sa surface, même en Australie! 4 >>> |
1687 Newton |
|
|
Le nombre imaginaire i |
Ce simple artifice d'écriture ( 5 >>> |
1750 Euler |
|
|
Caractéristique d'Euler |
Elle dit que: pour tous volume la quantité de faces, sommets et arêtes
constituent un invariant. Relation à la base de la topologie. 6 >>> |
1751 Euler |
|
|
La distribution normale ou loi de
Gauss |
La probabilité d'avoir une certaine valeur (la taille d'une personne,
par exemple) diminue fortement lorsqu'on s'éloigne de la moyenne. 7 >>> |
1810 Gauss |
|
|
L'équation d'onde |
Elle décrit la propagation d'une onde. Elle dit, par exemple, qu'une corde de guitare plus courte donne un
son plus aigu. Elle est utilisée partout où on rencontre des ondes: sismographie,
acoustique … 8 >>> |
1746 Jean Le Rond d'Alembert |
|
|
Transformée de Fourier |
Elle dit que toute onde peut être décrite par une succession de
sinusoïdes de fréquences différentes. Très utile en analyse spectrale, en compression de données … 9 >>> |
1822 Fourrier |
|
|
Équation de Navier-Stokes |
Permet les calculs d'aérodynamique ou d'hydrodynamique (bateaux et
avions); partout où il y a des fluides en mouvement (sang, par exemple) 10 >>> |
1845 Navier
et Stokes |
|
|
Équations de Maxwell |
Champ électrique et champ magnétique sont liés. L'un engendre l'autre. Base des communications hertziennes, radio, télévision, radar. 11 >>> |
1865 Maxwell |
|
|
La deuxième loi de la thermodynamique |
Le désordre (entropie) d'un système thermodynamique augmente toujours.
Un verre cassé ne se reformera pas spontanément. Permet le calcul des limites des possibilités du travail de la chaleur
(moteurs) 12 >>> |
1874 Boltzmann |
|
|
Formule de la relativité |
La masse des objets est de l'énergie. Permet de comprendre la quantité d'énergie libérée par la fission des
atomes. 13 >>> |
1905 Einstein |
|
|
Équation de Schrödinger |
En physique quantique, la matière peut se modéliser sous forme d'ondes
(et non de particules). Compréhension de l'atome. Application au laser par exemple. 14 >>> |
1927 Schrödinger |
|
|
Théorie de l'information |
Elle définit la quantité d'information dans un message, en se basant
sur les probabilités. Application aux codes de détection d'erreurs, en intelligence
artificielle ou encore en cryptographie. 15 >>> |
1949 Shannon |
|
|
Théorie du Chaos (loi
logistique) |
Elle exprime l'évolution des populations sous contrainte de ressources. La théorie du chaos dit qu'une petite sollicitation peut entraîner de
grands effets. Application à ma météorologie, aux tremblements de terre … 16 >>> |
1975 Robert May |
|
|
Équation de Black-Scholes |
Calcul de l'évolution de produits financiers. Application aux calculs de risques et de gain y compris en prévision à
long terme. 17 >>> |
1990 Black et Sholes |
|
![]()
|
Théorème de
Pythagore The
Pythagorean Theorem a²
+ b² = c²
Aire des deux carrés du haut = celle du carré du bas. |
Permet le
calcul de la longueur d'un côté d'un triangle
rectangle lorsqu'on connait la longueur des deux autres. Théorème
primordiale en géométrie
avec celui de Thalès
sur les proportions. Applicable en
géométrie euclidienne mais pas en géométrie
courbe. |
Pythagore est
un savant grec qui vivait autour des années
-500. Les Chinois et
les Babyloniens
connaissaient ce théorème avant Pythagore. |
Suite
>>>
|
Logarithmes Logarithms log x.y = log x + log y Exemple log10 (1 000 000) = 6 Car, il y a six "0" dans un
million. log10 = logarithme en base 10
|
La multiplication
est un raccourci de longues additions
(4 x 5 = 5 + 5 + 5 + 5); la puissance
est un raccourci de longues multiplications (54 = 5 x 5 x 5 x 5 =
625). Le nombre 625 = 54) donne idée de l'exponentielle
et l'exposant 4 donne une idée du logarithme.
Celui-ci, en gros, qualifie donc la taille d'un nombre. Les logarithmes
permettent le calcul sur des grandeurs de grande amplitude. Passage obligé
avant l'avènement des calculettes
et calculateurs. Fonction
réciproque de l'exponentielle. Une de leur
propriété fondamentale: transformer un produit en somme (cf. formule
indiquée). Évidemment la
règle à calcul a été supplantée par les calculettes. Par contre, les
logarithmes permettent la modélisation de phénomènes naturels de grande
dynamique: radioactivité, séismes
(échelle de Richter), sons (décibels). |
John Napier en
1610 ou 1614 Amélioré par
Henry Briggs (tables) Alors
qu'Oughtred en 1630 crée la règle à calcul. Napier ou Neper
en français a donné son nom aux logarithmes
népériens dont la base est la constante "e". |
Suite
>>>
|
Calcul différentiel Calculus
Volume
de la sphère par Archimède |
Permet le
calcul de grandeurs (surface, volume, vitesse …) appréhendables que par petits
pas. La formule
indiquée est la définition de la dérivée. Une notion de la vitesse de variation d'une grandeur.
Sa réciproque est le calcul
intégral: connaissant le rythme de changement en déduire l'évolution de
la grandeur. Invention
puissante puisqu'en une seule formule, elle résume toutes les données
astronomiques collectionnées depuis des millénaires et les trois lois de Kepler. Application aux
calculs de fusées aussi bien que de particules. |
Inventé au même
moment par Newton
et par Leibniz vers 1666 On retient la
modélisation de la gravité pour Newton, mais ce sont les notations de Leibniz
qui sont restées. |
Suite
>>>
|
Loi de gravitation Law of Universal Gravity
|
Tous les
objets ayant une masse
s'attirent mutuellement. C'est le cas de la Terre qui nous maintient
à sa surface, même en Australie! La loi de la
gravité indique avec quelle force deux objets s'attirent. Celle-ci décroit
très vite avec le carré
de la distance. Cette loi
explique parfaitement le mouvement des planètes. La
théorie de la relativité
générale englobe cette loi. |
Newton en 1687
Légende de la
pomme qui aurait créé le déclic de la compréhension du mouvement des
planètes. |
Suite
>>>
|
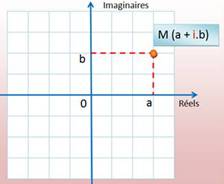
Le nombre
imaginaire i The square
root of -1
Représentation géométrique des nombres complexes |
Ce simple
artifice d'écriture permet la résolution de quantité de problèmes, notamment
la résolution des équations ou
encore en électronique,
en traitement du signal, mécanique
quantique … Ce nombre permet
la création des nombres
complexes, opération qui étend à deux dimensions la droite des réels. Les
quaternions
et les octavions sont des complexes à quatre et huit composantes. Euler établit
cette fameuse formule impliquant cinq nombres fondamentaux de l'algèbre. |
Euler en 1750. En 1545, Cardan
avait déjà imaginé les racines
de nombres négatifs pour résoudre des équations du 3e degré. En 1673, John
Wallis imagine les nombres complexes associés à un système d'axes; un axe
pour les réels et l'autre, orthogonal, pour les imaginaires . |
Suite
>>>
|
Relation d'Euler ou Caractéristique d'Euler Euler's Polyhedra Formula or Euler characteristic F – A + S = 2 6 – 12 + 8 = 2 pour le cube
|
Elle dit
que quel que soit le volume la quantité de faces moins la quantité de sommets
plus la quantité d'arêtes et un invariant. Généralisation
aux polyèdres troués (tore, bretzel …) et aux graphes.
Relation à la
base de la topologie,
la mathématique de la forme des objets: Notion d'invariance topologique. Application à
l'étude de l'ADN,
à la mécanique quantique … |
Euler en 1751. Découverte en 1639 par Descartes, mais
sans la publier. |
Suite
>>>
|
La distribution normale (gaussienne) Normal distribution
|
La probabilité
d'avoir une certaine valeur (la taille d'une personne, par exemple) diminue
fortement lorsqu'on s'éloigne de la moyenne. La courbe qui la
représente est une gaussienne ou courbe
en cloche (bell curve). Elle est
omniprésente en statistiques
(This curve is ubiquitous in statistics). Cette loi décrit
le comportement d'un grand
nombre d'"individus" indépendants. |
Gauss (1810). Application aux
sciences sociales en 1835 par Adolphe Quetelet qui découvre que les gens en
foule ont un comportement plus prédictible que pris individuellement. |
Suite
>>>
|
L'équation d'onde Wave équation
Aussi, cas du caillou jeté dans la mare. |
Elle
décrit la propagation d'une onde. Elle dit, par
exemple, qu'une corde de guitare plus courte donne un son plus aigu. Elle est
utilisée partout où on rencontre des ondes: sismographie, acoustique, thermodynamique
… C'est une
équation différentielle qui décrit les variations de l'onde avec le temps. Applications en
acoustique, optique ondulatoire … |
Jean Le Rond
d'Alembert (1746) |
Suite
>>>
|
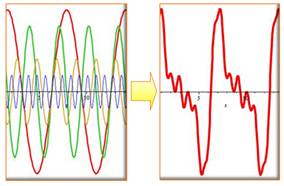
Transformée de Fourier Fourier Transform
En rouge à droite la sommes des quatre sinusoïdes
de gauche. |
Elle dit
que toute onde, même très compliquée comme la voix humaine, peut être décrite
par une somme
de sinusoïdes de paramètres différents. Très utile en
analyse spectrale, en traitement du signal, en compression de données … La Transformée
de Fourier est une opération mathématique qui permet de décomposer un signal
en ses composantes fréquentielles et de phases. Tout comme l’oreille humaine
peut décomposer les différentes fréquences d’un son, le spectre obtenu par la
Transformée de Fourier d’un signal représente l’intensité des différentes
composantes fréquentielles d’un signal. Elle calcule dans le même temps les
phases de chacune des composantes. Le cumul de ces différentes sinusoïdes
d’intensité et de phase données permet de reconstruire le signal (Transformée
de Fourier inverse). |
Fourrier en 1822
|
Suite
>>>
|
Équation de Navier-Stokes Navier-Stokes Equation
Sillage d'un sous-marin
en transit |
Elle
décrit le comportement des fluides en écoulement (normal, laminaire ou en
turbulences). À Gauche,
l'accélération du fluide; à droite, les forces exercées sur le fluide. Permet les
calculs d'aérodynamique ou d'hydrodynamique (bateaux, avions, automobiles …);
partout où il y a des fluides en mouvement (sang, par exemple) C'est une
équation non-linéaire aux dérivées partielles si difficile que les
mathématiciens n'ont pas la solution exacte. Des solutions approximatives
exigent des heures de calculs. Qui trouvera la solution sera récompensé par
un million de dollars (Clay). En 2014, elle semble en passe d'être trouvée. |
Navier et Stokes (1845) |
Suite
>>>
|
Équations de Maxwell Maxwell's Equations
|
Champ
électrique (E) et champ magnétique (H) sont liés. L'un engendre l'autre. Tout
tient dans ces quatre
équations différentielles. Base des
communications hertziennes, radio, télévision,
radar. Cette théorie
inclut l'optique ondulatoire comme cas particulier. Toutes les ondes
électromagnétiques, dont la lumière, se
propagent à la vitesse
de la lumière dans le vide. La mécanique
quantique explique le magnétisme à l'échelle microscopique et montrent que
ces équations sont des approximations mais qui marchent très bien à l'échelle
humaine. |
Maxwell(1865)
Concept de champ
introduit par Faraday, puis reformulée par Lorentz en 1895. En 1886, Hertz
découvre ces ondes. C'est Marconi en
1896 qui va réussir à les transmettre à distance. |
Suite
>>>
En
particulier, formulation différente des quatre équations.
|
La deuxième loi de la thermodynamique Second Law of Thermodynamics
La variation
d'entropie S est toujours positive ou sans changement à tous instant. Autrement-dit:
le désordre de la nature va globalement croissant.
|
Le
désordre (entropie S) d'un système
thermodynamique (sous influence de la chaleur) augmente toujours pour un
système fermé. Un verre cassé ne se reformera pas spontanément. Un corps
chaud cédera sa chaleur au corps froid jusqu'à ce qu'in équilibre de
température soit établi. La plupart des
lois sont réversibles. Celle-ci, non. Le sens du temps y est important. Permet le calcul
des limites des possibilités du travail
de la chaleur (moteurs) |
Boltzmann (1874) |
Suite
>>>
|
Formule de la relativité (une des -) Relativity E = m.c² (Forme réduite)
|
La matière contient
une énergie égale à sa masse multipliée
par le carré de la vitesse de la lumière. Permet de
comprendre la quantité d'énergie
libérée par la fission
des atomes. La relativité
restreinte ou générale a changé la perception du monde Restreinte: la
vitesse de la lumière est une constante une limite universelle; la notion de
temps est différente selon la vitesse. Générale:
l'espace incluant la dimension temps est courbe. Cette vision explique la
gravité dont la formulation date de Newton. La navigation GPS
n'existerait pas sans la théorie de la relativité. |
Einstein (1905) |
Suite
>>>
|
Équation de Schrödinger Schrödinger's Equation
Représentation classique de l'atome |
En physique quantique, la matière peut
se modéliser sous forme d'ondes (et non de particules). La relativité
explique le monde macroscopique; la mécanique quantique, via cette équation,
explique le monde microscopique. Une modélisation
pas très bien comprise par les savants, mais qui donne des résultats
étonnamment précis. C'est pourtant un calcul de probabilité
avec des nombres
complexes! Modélisation de
l'atome. Application au laser, semi-conducteurs, énergie nucléaire … |
Erwin Schrödinger
(1927)
|
Suite
>>>
|
Théorie de l'information Information theory
H est l'entropie
de la fonction p(x). Rappel: entropie = désordre.
|
Elle
définit la quantité d'information (entropie H)
dans un message, en se basant sur les probabilités. Pour un message
donné, elle indique le maximum de compression possible sans perdre
d'information. Application aux
codes de détection d'erreurs, en intelligence artificielle ou encore en
cryptographie. Cette notion est
à la base des calculs mathématiques appliqués aux informations et à leur
transmission. Application
aussi à l'intelligence
artificielle. La distribution normale est la loi de probabilité qui
maximalise l'entropie d l'information. Cette notion
établit une passerelle entre l'informatique et la physique. |
Claude Shannon
(1949) |
Suite
>>>
|
Théorie du Chaos (loi logistique) Chaos Theory (logistic map)
Attracteur
étrange de Lorenz |
Elle
exprime la valeur d'une population à la génération suivante dans le cas de
ressources contraintes. Curieusement,
pour certaines valeur de k, l'évolution de la population devient chaotique,
quasiment imprévisible. En commençant avec deux populations extrêmement
voisines, leurs évolutions seront totalement différentes. La théorie du
chaos dit qu'une petite sollicitation peut entraîner de grands effets (effet
papillon). Application à ma
météorologie, aux tremblements de terre … |
Robert May (1975) |
Suite
>>>
|
Équation de
Black-Scholes Black-Scholes
Equation
|
Calcul de
l'évolution de produits financiers. Cette équation
différentielle donne une base aux experts en finance et aux traders pour
calculer le prix des produits financiers qui sont sur le marché. Application aux
calculs de risques et de gain y compris en prévision à long terme. Ces calculs
malins n'ont pourtant pas empêché la
crise financière de 2008. |
Black et Sholes
(1990) |
Suite
>>>
|
Les trois
livres cités in fine (les trois premiers listés) sont du même genre. Huit
équations en commun: Pythagore, Newton
(gravité), Euler ( Chaque auteur cite au moins deux autres équations non mentionnées par les autres. On trouve, par exemples, chez les autres que Stewart:
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Sites |
|
|
Cette page |