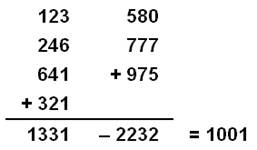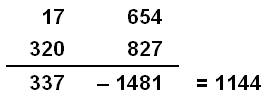|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 13 Méthode par tranches de milliers. La méthode est
valable pour tester la divisibilité d'un nombre par 7 ou par 11 ou par 13,
bénéficiant de la même propriété que chacun divise 1001. |
|
|
|||
|
Un nombre |
5 772 |
divisible par 13 ? |
|
|
Tranche
de milliers avec signe alterné (moins à droite) |
|
+ 005 – 772 767 |
|
|
Divisibilité
par 13 |
767 |
= 13 x 59 |
|
|
Inconvénient |
Il faut effectuer la division du dernier nombre
par 13. Pour un petit nombre autant diviser le nombre
lui-même. |
||
|
Un nombre |
1 604 938 257 |
divisible par 13 ? |
|
Tranche
de milliers avec signe alterné (moins à droite) |
|
+ 001 – 604 + 938 – 257 078 |
|
Divisibilité
par 13 |
78 |
= 13 x 6 |
|
Un nombre |
1 604 938 269 839 506 173 |
divisible par 13 ? |
|
Tranche
de milliers avec signe alterné (moins à droite) |
|
– 001 + 604 – 938 + 269 – 839 + 506 – 173 – 572 |
|
Divisibilité
par 13 |
572 |
= 13 x 44 |
Voir Démonstration
|
|
||
|
|
||
|
|
123 580 246 777 641 975 321 |
|
|
|
|
|
|
|
1001
= 7 x 11 x 13 |
|
|
|
17 654 320 827 |
|
|
|
|
|
|
|
114
+ 2x4 = 122 12
+ 2x2 = 16Non divisible apar 7 |
|
|
|
114
– 4 = 110 Divisible par 11 |
|
|
|
114
+ 4x4 = 130 Divisible par 13 |
|
English
|
Seven, eleven and thirteen are three
consecutive prime numbers. Their product is 1 001. The test is: separate the number
from the right to left in groups of 3 digits. Add the groups in even
positions and in odd positions. If the difference between sums is divisible
by 7, 11 or 13, the entire number is divisible by 7, 11 or 13 respectively. |
|
|
||
|
Méthode basée sur le fait
que: 4 x 10 – 1 = 39 = 3 x 13 Ajoutez quatre fois les
unités aux dizaines et recommencez avec le nombre obtenu. |
1283945 128394 + 4x5 = 128 414 12841 + 4x4 = 12 857 1285 + 4x7 = 1 313 131 + 4x3 = 143 14 + 4x3 = 26 = 2 x 13 Ce nombre est divisible par
13. |
|
Voir Cas
général
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi7D.htm
|
![]()