|
||||||||||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 11 Pour
trouver si un nombre est divisible par 11, il faut chercher son reste dans la
division par 11 et, constater qu'il est nul. Faire la division c'est bien,
mais c'est long ! Existe-t-il
une astuce pour aller plus vite, sans effectuer l'opération ? Oui, et elle
est relativement simple. Elle repose sur une particularité liant 11 à 100: 100
= 99 + 1 = 11 x
9 + 1 Il y
a un 11 caché dans 100 ! |
|
|
||
|
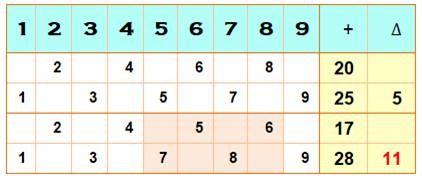
La
règle est illustrée par cet exemple => Un nombre est
divisible par 11 si la somme de ses chiffres de rang
pair soustraite de la somme de ses chiffres de rang impair est nulle ou un multiple de 11. |
|
|
|
Un
truc de calcul mental permet de traiter le nombre chiffre après chiffre. Exemple
précédent traité par
cette méthode => Autre exemple pour pratiquer 10864197531 1086419752 108641973 10864194 1086415 108636 (41 – 5 = 36) 10857 (63
– 6 = 57) 1078 (85
– 7 = 78) 99 (107
– 8 = 99) Ce
nombre est divisible par 11 |
Méthode
par itérations sur le chiffre des unités, dite aussi critère dominos.
Voir Critères
de divisibilité domino pour d'autres nombres |
|
Propriétés
amusantes
|
Un nombre palindrome
ou, a fortiori, un repdigit ayant une quantité paire de
chiffres est divisible par 11. C'est
le cas d'un nombre concaténé à son retourné.
Le quotient est un nombre palindrome. Exemples: N = 123321; P = 1+3+2 = 6
; I = 2+3+1 = 6; P – I = 0. 123321
= 11 x 11211 N = 777777; P = 7+7+7 = 21 ; I = 7+7+7 = 21; P – I = 0.
777777 = 11 x 70707 456 => N = 456 654 = 11 x 41 514 Un nombre
de deux chiffres ajouté à son retourné est divisible par 11. Exemple: 23 + 32 = 55 = 5 x 11. >>> Un nombre ajouté à son retourné est divisible par
11 si la quantité de chiffres est paire. Exemple 1289 + 9821 = 11 110 567891 + 198765 = 766 656 = 11 x 69
696 Les nombres en aa…abb..b avec une
quantité paire de chiffres sont divisibles par 11. Exemple:
88889999 = 11 x 8080909 |
Nombres de quatre chiffres divisibles par 11
|
Trois
chiffres sur quatre sont fixés. Quel
est le quatrième pour que le nombre soit divisible par 11? Exemples 123x
=> 1 + 2 = 4 et 2 + x = 4 => x = 2. En effet: 1232 = 11 x 112 5x26
=> 5 + 2 = 7 et x + 6 = 7 => x = 1. En effet: 5126 = 11 x 466 |
Voir Divisibilité par
11, 101, 111 …
![]()
Explications détaillées
|
|
|
|
Exemples:
Chaque fois que l'on peut trouver un multiple de
11, on l'élimine. Parfois, on ajoute 11, pour éviter un nombre
négatif. L'astuce que nous allons examiner, consiste à
considérer les puissances de 10. |
|
Voir Modulo
|
|
|
|
Le reste de la division par 11 de 10n est |
|
|
|
|
|
Exemples: 13 =>
13 – 11 = 2 25 =>
25 – 22 = 3 100
=> 100 – 99 = 1
Racine
numérique par 11 de 100 = R11 (100) = 1. Formalisation
pour un nombre N
Voir Numération / Système décimal
Règle
Exemple N
= 123456 R11
= (6 + 4 + 2) – (5 + 3 + 1) = 12 – 9 = 3 En
effet:
123456 = 11 223 x 11 + 3 Méthode
alternative (plus pratique)
Exemple N
= 123456 R11
= (6 - 5) + (4 - 3) + (2 - 1) = 1 + 1 + 1 = 3
Exemple
pratique N
= 4 993 260 817 R11 = ?
|
|
|
|
|
|
Un nombre est
divisible par 11 si sa racine
numérique par 11 est nulle. Exemple général N
= 181 907 R11
= (8-1) + (9-1) + (7-0) = 7 + 8 + 7 = 22 => 0 Divisible par 11. Exemple avec
divisibilité reconnaissable au premier coup d'œil N
= 333 333 R11
= (3-3) + (3-3) + (3-3) = 0 => Divisible par 11. N
= 484 R11
= 4 + 4 – 8 => Divisible par 11. N
= 913 R11
= 9 + 3 – 1 => Divisible par 11. |
|
Méthode par tranche de milliers
|
Cette
méthode, valable pour les divisibilités par 7, 11
et 13, consiste à faire la somme des tranches paires de milliers diminuée de
la somme des tranches impaires. Ex: 1
358 024 679 Ou
1012 avec méthode classique |
|
Aucun
nombre dont les chiffres se suivent n'est divisible par 11. 123456
=> 1 + 3 + 5 = 9 et 2 + 4 + 6 = 12. Exemple généralisable. |
|
|
|
|
Principe
Procédé
On
compare à la racine du résultat de la vraie opération.
|
|
Voir Fondements de la preuve par 11
|
|
|
|
Tous les nombres
en abba sont divisibles
par 11.
Tous les nombres, somme d'un nombre ayant une quantité paire
de chiffres
et de son retourné, sont divisibles
par 11. Voir Premiers de Luhn
Tous les nombres
en aaaa sont divisibles
par 11 et par 101.
4554
= 11 x 414 Tous les nombres
palindromes à quantité paire de chiffres sont divisibles
par 11.
123123
= 11 x 11 193 Tous les nombres à
répétition d'un groupe de chiffres en quantité
impaire sont divisibles
par 11. |
|
|
|
||
|
|
30+3 – 44x0+2 = 33
– 42 = 27 – 16 = 11 La divisibilité est vraie pour n= 0. |
|
|
|
3(n+1)+3 – 44(n+1)+2 = 3n+4
– 44n+6 |
|
|
|
= 3n+3 x
3 – 44n+2 x 44 |
|
|
|
= 3n+3 x 3 – 44n+2 x 256 = 3n+3 x 3 – 44n+2 x (253 + 3) = (3n+3 – 44n+2) x
3 + 44n+2 x 253 Chance? 253 = 11 x 23 |
|
|
|
= (3n+3 – 44n+2) x
3 + 44n+2
x 11 x 23 |
|
|
|
(3n+3 – 44n+2) x 3 + 44n+2
x 11 x 23 Si ce premier terme est divisible par 11, alors
toute l'expression est divisible par 11. |
|
|
|
|
|
|
3n+3 – 44n+2 La relation de divisibilité est vraie pour
d'autres valeurs des termes additifs en rose. |
Si 0 et 0 + 5k
divisible par 11 Si 1 et 4 + 5k
divisible par 11 Si 2 et 3 + 5k
divisible par 11 Si 3 et 2 + 5k
divisible par 11 … Divisible par 77 pour {0, 0}P, {1,
4}I, {2, 8}P,
{3, 12}I, {4, 1}P… L'indice impose que n soit
pair ou impair. |
|
Voir Démonstration
par récurrence
|
|
||
|
Les deux nombres pannumériques les plus simples
ne sont pas divisibles par 11. |
123 456 789 ou 987654321 p = 2 + 4 + 6 + 8 = 20 q = 1 + 3 + 5 + 7 + 9 = 25 s = p + q = 45 |
|
|
Min et Max Quel est
le plus grand nombre pannumérique divisible par 11? Le plus petit? Une recherche qui allie:
La somme de tous les chiffres est s = 45. Quelles
sont les valeurs de p et q telles que
p + q = 45 et p – q = 0 mod 11. Deux possibilités: La somme 1 + 2 + 3 + 4 + 0 = 10 est supérieure à 6; le premier couple
est éliminé. Le tableau montre comment parvenir à la solution
en testant les derniers chiffres. En procédant de la même manière, on trouve les
plus petits avec ou sans le 0. Solution un peu plus difficile à trouver. Sur les 10!
= 3 628 800 permutations des dix chiffres, 316 800 sont divisibles par
11. Pannumériques partiels et divisibilité par 11 QtéDiv. = quantité de
nombres avec les chiffres 1, 2, 3 divisibles par 11 Total = quantité de nombres
avec ces chiffres Min et max: le plus petit et
le plus grand divisibles par 11.
|
987 652
413 = 11 x 89 786 583 9 876 524 130 = 11 x 897 865 830 Les plus grands pannumériques divisibles par 11
À partir de la configuration maximale montrant un écart de 5, on passe
à la configuration du dessous en remarquant qu'il faut retirer 3 à 20 et
ajouter 3 à 25. 123 475
869 = 11 x 11 225 079 Le plus petit pannumérique divisible par 11 (sans
0)
1 024 375 869 = 11 x 93 125 079 Le plus petit pannumérique divisible par 11 (avec
0)
Le 0 est placé juste après le 1 pour le rendre significatif. Ayant placé les 1, 2, 3 et 4, il faut faire 7 en deux nombres plus
grands que 4, ce qui est impossible. Ayant placé les 1, 2 et 3, il faut faire 11, ce qui est faisable
uniquement avec 5 et 6. Le reste découle naturellement. |
|
|
|
||
|
Nombres
les plus petits et les plus grands par tranche de puissances de 10. Q: quantité de chiffres (tranche 10Q-1
à 10Q) R: le rang du nombre dans sa tranche |
||
|
Sans le 0
|
Avec le 0
|
|
![]()
|
|
|
|
Nombre de trois chiffres successifs
divisibles par 11 [liste des chiffres], quantité de nombres
divisibles par 11, [les nombres] [1, 2, 3], 2, [231, 132] Seuls nombres à trois chiffres successifs
divisibles par 11 [2, 3, 4], 0, [] [3, 4, 5], 0, [] [4, 5, 6], 0, [] [5, 6, 7], 0, [] [6, 7, 8], 0, [] [7, 8, 9], 0, [] [8, 9, 0], 0, [] Nombre de quatre chiffres
successifs divisibles par 11 [1, 2, 3, 4], 8, [3421, 2431, 4312, 1342, 4213,
1243, 3124, 2134] [2, 3, 4, 5], 8, [4532, 3542, 5423, 2453, 5324,
2354, 4235, 3245] [3, 4, 5, 6], 8, [5643, 4653, 6534, 3564, 6435,
3465, 5346, 4356] [4, 5, 6, 7], 8, [6754, 5764, 7645, 4675, 7546,
4576, 6457, 5467] [5, 6, 7, 8], 8, [7865, 6875, 8756, 5786, 8657,
5687, 7568, 6578] [6, 7, 8, 9], 8, [8976, 7986, 9867, 6897, 9768,
6798, 8679, 7689] [7, 8, 9, 0], 0, [] Nombre de cinq chiffres successifs
divisibles par 11 [1, 2, 3, 4, 5],
0, [] [2, 3, 4, 5, 6], 12, [56342, 36542, 54362, 34562,
56243, 26543, 54263, 24563, 36245, 26345, 34265, 24365] [3, 4, 5, 6, 7], 12, [74635, 64735, 73645, 63745,
74536, 54736, 73546, 53746, 64537, 54637, 63547, 53647] [4, 5, 6, 7, 8], 12, [68574, 58674, 67584, 57684,
68475, 48675, 67485, 47685, 58476, 48576, 57486, 47586] [5, 6, 7, 8, 9], 12, [97856, 87956, 95876, 85976,
97658, 67958, 95678, 65978, 87659, 67859, 85679, 65879] [6, 7, 8, 9, 0],
14, [98076, 97086, 89067, 86097, 79068, 76098, 68079, 67089, 79860, 68970,
97680, 67980, 86790, 76890] Nombre de six chiffres successifs
divisibles par 11 [1, 2, 3, 4, 5,
6], 0, [] [2, 3, 4, 5, 6,
7], 0, [] [3, 4, 5, 6, 7,
8], 0, [] [4, 5, 6, 7, 8,
9], 0, [] [5, 6, 7, 8, 9,
0], 60, [560879, 560978, 567809,
567908, 580679,
580976, 587609,
587906, 590678,
590876, 597608,
597806, 608597,
608795, 609587,
609785, 658097,
658790, 659087,
659780, 678095, 678590, 679085, 679580, 760859, 760958,
765809, 765908,
780659, 780956, 785609,
785906, 790658, 790856, 795608,
795806, 806597,
806795, 809567,
809765, 856097,
856790, 859067,
859760, 876095,
876590, 879065,
879560, 906587,
906785, 908567,
908765, 956087,
956780, 958067,
958760, 976085,
976580, 978065,
978560] Nombres pairs ou impairs [1, 3, 5, 7], 8,
[1375, 1573, 3157,
3751, 5137,
5731,
7315, 7513] [2, 4, 6, 8], 8, [2486, 2684, 4268, 4862, 6248,
6842, 8426, 8624] [2, 4, 6, 8, 0], 16, [24068, 24860,26048, 26840, 42086 42680 48026,
48620, 62084, 62480, 68024, 68420, 84062, 84260, 86042, 86240] |
|
![]()
|
|
|||||||||||
|
Observons la division
posée. 279 / 11 = 25,363636… |
|
||||||||||
|
Prenons le problème à l'envers:
quels sont les nombres qui produisent une répétition de deux chiffres ?
Essayons avec l'exemple précédent. En soustrayant ce nombre de cent fois lui-même,
il ne reste que le nombre entier formé des deux chiffres (36). |
|
||||||||||
|
On en déduit la fraction pour n dans le cas de notre
exemple ou, en généralisant, pour ab. |
|
||||||||||
|
Or, la fraction 1/99 est spéciale: |
|
||||||||||
|
En multipliant par 9, on obtient une relation de
base pour le 1 divisé par 11. |
|
||||||||||
|
Pour tous les nombres de 1 à 10, on aura les
multiples de 090909… . Et ce sont les multiples de 9, évidemment. |
1
/ 11 = 0,090909… 2
/ 11 = 0,181818… 3
/ 11 = 0, 272727… … 10
/ 11 = 0,909090… |
||||||||||
|
La fraction avec 11 est triviale. |
11
/ 11 = 1 |
||||||||||
|
La fraction avec 12 se comporte de la façon
suivante: |
|
||||||||||
|
Les nombres suivants produisent une constante
suivie des mêmes fractions que celles obtenues pour les nombre de 1 à 10. |
|
||||||||||
|
Notez que l'on a la même
propriété avec la division par 99. Si ab est un nombre de 1 à 98, la division
est sympathique. |
Exemple 56
/ 99 = 0,565656… |
||||||||||
![]()
|
Suite |
|
|
Autour du 11 |
|
|
Suite |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi11.htm |
![]()