NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/12/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISION
Débutants Division	Divisibilité			Glossaire Division
INDEX Divisibilité	Introduction	Critères généraux	Racine numérique
	Preuve par neuf	Clés de divisibilité	Divisibilité par tranches
	Par 7	Divisibilité par 2, 3, … 137 …	Divisibilité Dominos
		Sommaire de cette page Méthode des empreintes >>> Truc avec 7 >>> Explications >>> Cas de 11 >>> Quelques clés Méthode de l'unité tronquée >>> Divisibilités vues par les unités (Dominos) >>> Critère de divisibilité par l'unité

Clés de DIVISIBILITÉ

ou empreintes de divisibilité

En exprimant un nombre sous sa forme générique en décimal, il est possible de caractériser son comportement lors d'une division par k.

Par ce procédé, le nombre laisse une empreinte caractéristique appelée clé de divisibilité.

Cette astuce pour reconnaître la divisibilité d'un nombre est due à Pascal (1654).

Je conseille de lire au préalable: Introduction à la divisibilité

TRUC avec 7
Effectuons la division par 7 du nombre 1. Notons les restes à chaque étape. On s'arrête lorsqu'on retrouve 1 pour reste (alors, le quotient se répète).
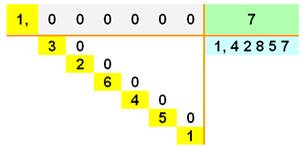
Clé du 7 (les restes en jaune) Les chiffres se répètent à l'infini.	1 3 2 6 4 5 1 2 …
Critère de divisibilité par 7.	Un nombre est divisible par 7 si la somme pondérée par la clé de tous ses chiffres est divisible par 7.

Voir Exemples et explications / Méthodes pratiques pour 7

CAS de 11
Division de 1 par 11
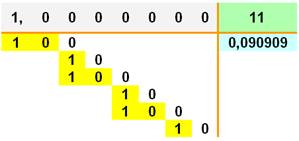
Clé du 11 (les restes en jaune) Ou en écart à 11, alors 10 devient – 1	10, 1, 10, 1, 10… – 1, 1, – 1, 1, – 1 …
Critère de divisibilité par 7.	Un nombre est divisible par 11 si la somme alternée de ses chiffres est divisible par 11.

On retrouve la règle bien connue

QUELQUES CLÉS
Exemple d'application divisibilité de 4 144 par 37 ? Remarques La clé de divisibilité offre un procédé général pour tester la divisibilité par k. Mais cela est parfois laborieux. Il existe souvent des procédés plus pratiques. Le procédé est valable pour tester la divisibilité par un nombre premier. Pour un nombre composé, le test portera sur les tous les facteurs.

Voir Critères généraux de divisibilité

Divisibilité vue par les unités - Dominos
Il existe une méthode générale qui consiste à examiner l'unité du nombre (U) et la quantité totale de ses dizaines (D). Critères dominos ou méthode itérative sur le chiffre des unités.	N = 10D + U
Supposons que ce nombre est divisible par d.	N = 10D + U = d . n
Le but est d'associer U et D de la manière suivante: La somme de D et d'un multiple de l'unité U doit être divisible par d.	D + c.U = d . m
Prenons c fois la première égalité, et l'autre égalité telle quelle.	10D.c + c.U = c . d . n D + c.U = d . m
Différence entre les deux:	D (10c – 1) = d (c.n – m) = d . l
Pour obtenir cette égalité quel que soit D:	10c – 1 doit être divisible par d
Exemples
Prenons les cas de d = 7:	10c – 1 = 7 l
Égalité satisfaite pour c = –2:	10 (–2) – 1 = –21
Exemple avec N= 154	X = 15 et Y = 4 15 – 2 x 4 = 15 – 8 = 7 Divisible par 7
Prenons les cas de d = 37:	10c – 1 = 37 l
Égalité satisfaite pour c = –11:	10 (–11) – 1 = –111 = – 3 x 37
Exemple avec N= 2 442	X = 244 et Y = 2 244 – 22 = 222 22 – 22 = 0 Divisible par 37
Truc pour calculer la valeur de c: Trouvez le plus petit multiple en 1 de d; Prenez pour c le négatif des dizaines Si plus pratique prenez le complément à d.	13 x 7 = 91 c = – 9 c' = 13 – 9 = 4
Autre exemple avec 71: cela pourrait paraître compliqué pour un tel nombre premier. Pourtant la clé est immédiatement trouvée.	71 x 1 = 71 c = –7 c' = 71 – 7 = 64
Note: effectivement, la clé complémentaire c' = (d – c) fonctionne aussi. Pour 7, il s'agit de c = –2 et son complémentaire c' = +5. Pour 43, la clé est 13, mais son complémentaire -30 est beaucoup plus simple à utiliser.	154 donne 15+ 5x4 = 35 divisible par 7. 989 donne 98 – 30x9 = – 172 divisible par 43.
Cas typique pour 19: le tableau indique -17, il sera plus facile de calculer avec 19 – 17 = 2.	8 664 donne 866 + 2x4 = 874 87 + 2x4 = 95 et 95 = 5 x 19

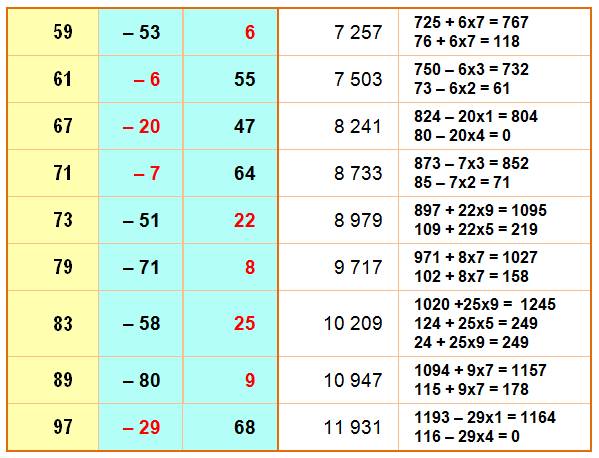
Critères de divisibilité par l'unité – Critère dominos / Méthode itérative sur le dernier chiffre

La valeur de c ou c' mise en rouge est généralement la plus pratique.

Note: il est parfois plus facile de prendre le complément.

Ainsi pour 19, la clé est -17, on peut prendre + 2, plus facile à calculer.

Suite	Divisibilité par 2, 3, 4, … Divisibilité par 7 Preuve par neuf Somme des chiffres de diverses natures Divisibilité – Index
Voir	Calcul mental – Index Formes polynomiales Géométrie – Index Modulo Nombres abondants  Nombres parfaits  Nombres périodiques Théorie des nombres – Index
DicoNombre	Nombres 37, 137, 1001 et leurs curiosités Nombre 249
Site	Simple divisibility rules for the 1st 1000 prime numbers – C. C. Briggs – 1999
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiCl.htm