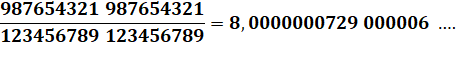|
|||||||||||||||||||||||||||||
![]()
|
NOMBRE 123 456 789 Multiplication
et division des pannumériques tronqués, directs
ou retournés. |
|
et son retourné 987654321 |
|
|
Table
de multiplication des pannumériques tronqués Directs 1 12 123 1
234 12 345 123 456 1 234 567 12 345 678 123 456 789 2 2 24 246 2
468 24 690 246 912 2 469 134 24 691 356 246 913 578 3 3 36 369 3 702 37
035 370 368 3 703 701 37
037 034 370 370 367 4 4 48 492 4
936 49 380 493 824 4 938 268 49 382 712 493 827 156 5 5 60 615 6
170 61 725 617 280 6 172 835 61 728 390 617 283 945 6 6 72 738 7 404 74
070 740 736 7 407 402 74
074 068 740 740 734 7 7 84 861 8
638 86 415 864 192 8 641 969 86 419 746 864 197 523 8 8 96 984 9
872 98 760 987 648 9 876 536 98 765 424 987 654 312 9 9 108 1 107 11 106 111
105 1 111 104 11 111 103 111 111
102 1 111 111 101 Retournés 9 98 987 9
876 98 765 987 654 9 876 543 98 765 432 987 654 321 2 18 196 1 974 19
752 197 530 1 975 308 19 753 086 197 530 864 1 975 308 642 3 27 294 2
961 29 628 296 295 2 962 962 29 629 629 296 296 296 2
962 962 963 4 36 392 3 948 39
504 395 060 3 950 616 39 506 172 395 061 728 3 950 617 284 5 45 490 4 935 49
380 493 825 4 938 270 49 382 715 493 827 160 4 938 271 605 6 54 588 5
922 59 256 592 590 5 925 924 59 259 258 592 592 592 5
925 925 926 7 63 686 6 909 69
132 691 355 6 913 578 69 135 801 691 358 024 6 913 580 247 8 72 784 7 896 79
008 790 120 7 901 232 79 012 344 790 123 456 7 901 234 568 9 81 882 8 883 88 884 888
885 8 888 886 88 888 887 888 888
888 8 888 888 889
|
|
|
|
|
|
123 456
=> 7/3 = 2,333… sa partie entière est 2. Ça
semble marcher. Et effectivement ça marche! Un pannumérique,
complet ou tronqué, multiplié par un multiple de 3 (k), est voisin d'un
nombre périodique; la différence est égale au produit de k par l'unité du
pannumérique plus 1, divisé par 9, différence dont on ne prend que la partie
entière.
Puis
les valeurs de la partie entière des divisions par 9 Exemple de lecture (cases jaunes) 123 456 x 12 = 1 481 472; Ici, unité = 6 et k = 12. 7
x 12 / 9 = 9,333 … => 9 |
|
|
1 |
12 |
123 |
1
234 |
12
345 |
123
456 |
1
234 567 |
12
345 678 |
123
456 789 |
|
|
3 |
3 |
36 |
369 |
3 702 |
37 035 |
370 368 |
3 703 701 |
37 037 034 |
370 370 367 |
|
6 |
6 |
72 |
738 |
7 404 |
74 070 |
740 736 |
7 407 402 |
74 074 068 |
740 740 734 |
|
9 |
9 |
108 |
1 107 |
11 106 |
111 105 |
1 111 104 |
11 111 103 |
111 111 102 |
1 111 111 101 |
|
12 |
12 |
144 |
1 476 |
14 808 |
148 140 |
1 481 472 |
14 814 804 |
148 148 136 |
1 481 481 468 |
|
15 |
15 |
180 |
1 845 |
18 510 |
185 175 |
1 851 840 |
18 518 505 |
185 185 170 |
1 851 851 835 |
|
18 |
18 |
216 |
2 214 |
22 212 |
222 210 |
2 222 208 |
22 222 206 |
222 222 204 |
2 222 222 202 |
|
21 |
21 |
252 |
2 583 |
25 914 |
259 245 |
2 592 576 |
25 925 907 |
259 259 238 |
2 592 592 569 |
|
24 |
24 |
288 |
2 952 |
29 616 |
296 280 |
2 962 944 |
29 629 608 |
296 296 272 |
2 962 962 936 |
|
27 |
27 |
324 |
3 321 |
33 318 |
333 315 |
3 333 312 |
33 333 309 |
333 333 306 |
3 333 333 303 |
|
Écart |
|||||||||
|
3 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
|
|
6 |
2 |
2 |
3 |
4 |
4 |
5 |
6 |
6 |
|
|
9 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
12 |
4 |
5 |
6 |
8 |
9 |
10 |
12 |
13 |
|
|
15 |
5 |
6 |
8 |
10 |
11 |
13 |
15 |
16 |
|
|
18 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
21 |
7 |
9 |
11 |
14 |
16 |
18 |
21 |
23 |
|
|
24 |
8 |
10 |
13 |
16 |
18 |
21 |
24 |
26 |
|
|
27 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
|
|
Somme |
|||||||||
|
3 |
37 |
370 |
3 703 |
37 037 |
370 370 |
3 703 703 |
37 037 037 |
370 370 370 |
|
|
6 |
74 |
740 |
7 407 |
74 074 |
740 740 |
7 407 407 |
74 074 074 |
740 740 740 |
|
|
9 |
111 |
1 111 |
11 111 |
111 111 |
1 111 111 |
11 111 111 |
111 111 111 |
1 111 111 111 |
|
|
12 |
148 |
1 481 |
14 814 |
148 148 |
1 481 481 |
14 814 814 |
148 148 148 |
1 481 481 481 |
|
|
15 |
185 |
1 851 |
18 518 |
185 185 |
1 851 851 |
18 518 518 |
185 185 185 |
1 851 851 851 |
|
|
18 |
222 |
2 222 |
22 222 |
222 222 |
2 222 222 |
22 222 222 |
222 222 222 |
2 222 222 222 |
|
|
21 |
259 |
2 592 |
25 925 |
259 259 |
2 592 592 |
25 925 925 |
259 259 259 |
2 592 592 592 |
|
|
24 |
296 |
2 962 |
29 629 |
296 296 |
2 962 962 |
29 629 629 |
296 296 296 |
2 962 962 962 |
|
|
27 |
333 |
3 333 |
33 333 |
333 333 |
3 333 333 |
33 333 333 |
333 333 333 |
3 333 333 333 |
|
|
|
|||
|
Exploitation de deux
propriétés de toute beauté. |
Relation
simple entre le pannumérique et son retourné:
Simplification singulière
des fractions
|
||
|
= 8,0000000729 000006 …. |
|||
|
Curiosité |
Si vous faites cette
opération sur votre calculette vous obtenez généralement 8,0000001. Sur celle de votre ordinateur en
mode standard, vous avez |
|
|
|
Duplication |
|
||
|
Notez que ces nombres sont divisibles par 9 |
|
||
Tableau
montrant les divisions successives A/B (pour information)

2
![]()
|
Suite Retour |
|
|
Voir |
|
|
Cette page |
![]()